四川省成都武侯区领川外国语学校2023-2024学年七年级下册3月月考数学试题（含解析）

这是一份四川省成都武侯区领川外国语学校2023-2024学年七年级下册3月月考数学试题（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分）
1．下列计算正确的是（ ）
A．m4+m3＝m7B．（m4）3＝m7
C．m（m﹣1）＝m2﹣mD．2m5÷m3＝m2
2．如图，下列条件中，不能判定的是（ ）

A．B．
C．D．
3．某种计算机完成一次基本运算的时间约为1纳秒，已知1纳秒=0.000000001秒，该计算机完成15次基本运算，所用时间用科学记数法表示为（ ）
A．秒B．秒C．秒D．秒
4．下列生活实例中，数学原理解释错误的一项是( )
A．从一条河向一个村庄引一条最短的水渠，其中数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线
B．两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短
C．把一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线
D．从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连接直线外一点与直线上各点的所有线段中，垂线段最短
5．下列各式中，为完全平方式的是（ ）
A．B．C．D．
6．若，，则等于（ ）
A．B．6C．21D．20
7．若，，则代数式的值是（ ）．
A．89B．C．67D．
8．如图，边长为a的大正方形剪去一个边长为b的小正方形后，将剩余部分通过割补拼成新的图形，根据图形能验证的等式为（ ）
A．B．
C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9．若，，那么式子 .
10．一个角的补角是它的余角的倍，则这个角是 ．
11．若关于的二次三项式是完全平方式，则的值为 ．
12．如图，在△ABC中，BE、CE 分别是∠ABC 和∠ACB 的平分线，过点 E 作 DF∥BC，交 AB 于 D，交 AC 于 F，若 AB＝5，AC＝4，则△ADF周长为 ．
13．，则 ．
三、解答题
14．计算：
(1)
(2)
15．先化简，再求值：，其中，．
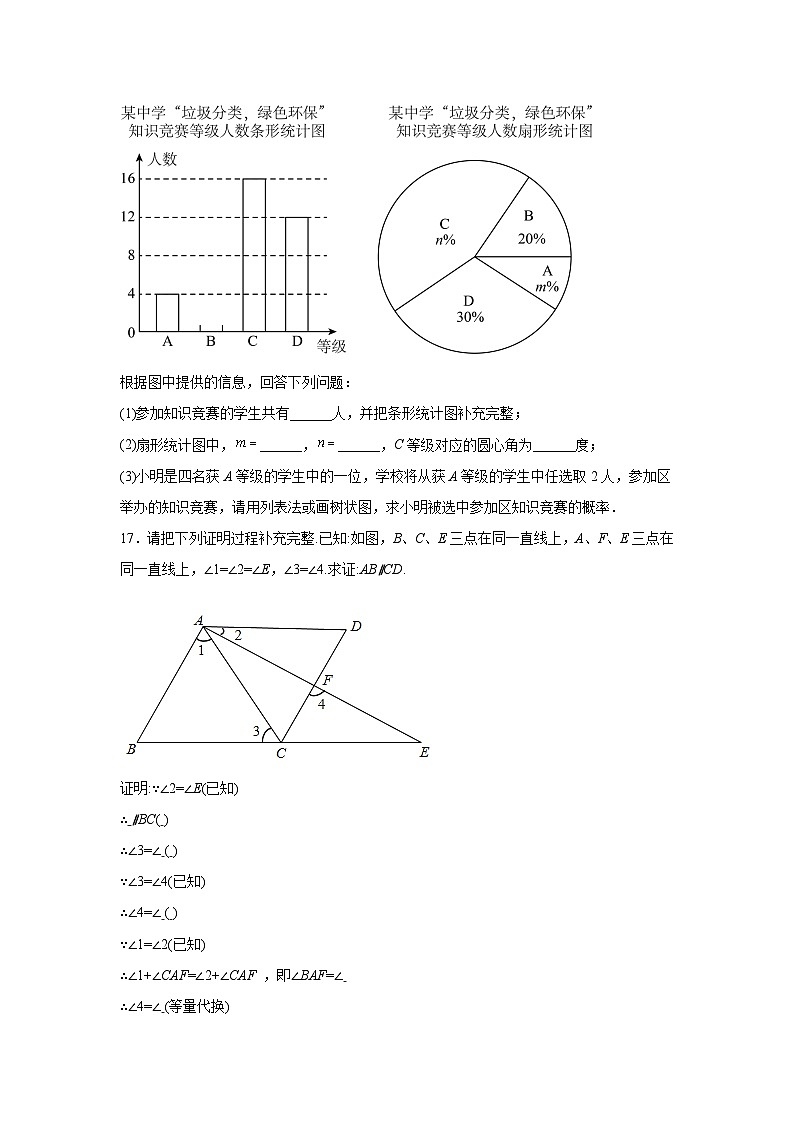
16．某中学举行了“垃圾分类，绿色环保”知识竞赛活动，根据学生的成绩划分为A，B，C，D四个等级，并绘制了不完整的两种统计图：
根据图中提供的信息，回答下列问题：
(1)参加知识竞赛的学生共有______人，并把条形统计图补充完整；
(2)扇形统计图中，______，______，C等级对应的圆心角为______度；
(3)小明是四名获A等级的学生中的一位，学校将从获A等级的学生中任选取2人，参加区举办的知识竞赛，请用列表法或画树状图，求小明被选中参加区知识竞赛的概率．
17．请把下列证明过程补充完整.已知:如图，B、C、E三点在同一直线上，A、F、E三点在同一直线上，∠1=∠2=∠E，∠3=∠4.求证:AB∥CD.
证明:∵∠2=∠E(已知)
∴ ∥BC( )
∴∠3=∠ ( )
∵∠3=∠4(已知)
∴∠4=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF ，即∠BAF=∠
∴∠4=∠ (等量代换)
∴ ( )
18．如图，平分平分．

(1)请判断与的位置关系并说明理由．
(2)如图，在（1）的结论下，当保持不变，移动直角顶点E，使，当直角顶点E点移动时，问与是否存在确定的数量关系？并说明理由．

(3)如图，在（1）的结论下，P为线段上一定点，点Q为直线上一动点，当点Q在射线上运动时（点C除外）与有何数量关系？请写出你的结论并证明．

B卷（共50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19．在同一平面内，若与的两边分别垂直，且比的3倍少，则的度数为 ．
20．多项式 4x2﹣12xy+10y2+4y﹣12的最小值是 ．
21．若条直线两两相交于不同的点时，可形成 对对顶角．
22．已知多项式为被除式，除式为，商式为，余式为1，则这个多项式为 ．
23．我国古代数学家杨辉发现了如图所示的三角形，我们称之为“杨辉三角”．从图中取一列数：，，，，…，记，，，，，那么的值是 ．
二、解答题（本大题共3个小题，共30分．）
24．观察下列各式，寻找规律：
已知x≠1，计算：
（x﹣1）（1+x）＝x2﹣1
（x﹣1）（1+x+x2）＝x3﹣1
（x﹣1）（1+x+x2+x3）＝x4﹣1
（x﹣1）（1+x+x2+x3+x4）＝x5﹣1
…
（1）根据上面各式可得规律：（x﹣1）（1+x+x2+x3+…+xn）＝ .
（2）根据(1)中规律计算1+2+22+23+24+…+22018 的值.
（3）求314+315+…+3100的个位数字.
25．随着智能手机的普及，网购已经成为人们的一种生活方式，快递业也随之发展壮大。某快递公司每件普通物品的收费标准如下表：
例如：寄往市内一件千克的物品，运费总额为：元．寄往市外一件千克的物品，运费总额为：元．
(1)小华同时寄往市内一件千克的物品和市外一件千克的物品，各需付运费多少元？
(2)小彤同时寄往市内和市外同一件千克的物品，已知超过，且的整数部分是，小数部分小于，请用含字母的代数式表示市外与市内这两笔运费的差．
(3)某日小华和小彤同时在该快递公司寄物品，小华寄往市外，小彤寄往市内，小彤所寄物品的重量不是整数，小华的运费比小彤的运费多元，物品的重量比小彤多千克，则小华和小彤共需付运费多少元？
26．如图，点为直线上一定点，作射线．
(1)如图1，当射线在直线的下方时，在直线的同侧作射线，使．将射线绕着点逆时针旋转得到射线．
①若时，求的度数．
②当时，若，求的值．
(2)如图2，若，射线从开始绕着点以每秒的速度逆时针旋转至结束，设旋转时间为．在旋转过程中，同时将射线绕着点逆时针旋转得到射线，作射线平分，当为定值时，求的取值范围及对应的定值．（本题中研究的角均为大于且小于的角）
参考答案与解析
1．C
【分析】根据各个选项中的式子可以计算出正确的结果，从而可以解答本题．
【解答】解：m4+m3不能合并，故选项A错误；
（m4）3＝m13，故选项B错误；
m（m﹣1）＝m2﹣m，故选项C正确；
2m5÷m3＝2m2，故选项D错误；
故选：C．
【点拨】本题主要考查了单项式乘以多项式，幂的乘方，同底数幂的除法，准确计算是解题的关键．
2．C
【分析】根据同位角相等两直线平行；内错角相等两直线平行；同旁内角互补两直线平行；进而判断即可．
【解答】根据，可得；
根据，可得；
根据，可得；
根据，可得；
故选：C．
【点拨】本题考查平行线的判定定理，熟练掌握平行线的判定定理是解题的关键．
3．C
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】所用时间=15×0.000000001=1.5×10-8（秒）．
故选：C．
【点拨】此题考查科学记数法表示较小的数，一般形式为，其中，n为由原数左边起第一个不为零的数字前面的0的个数所决定．
4．A
【分析】根据垂线段最短、直线和线段的性质即可得到结论．
【解答】解：A、从一条河向一个村庄引一条最短的水渠，其中数学原理是：垂线段最短，故原命题错误；
B、两个村庄之间修一条最短的公路，其中的数学原理是：两点之间线段最短，正确；
C、一个木条固定到墙上需要两颗钉子，其中的数学原理是：两点确定一条直线，正确；
D、从一个货站向一条高速路修一条最短的公路，其中的数学原理是：连接直线外一点与直线上各点的所有线段中，垂线段最短，正确．
故选A．
【点拨】考查了垂线段最短，直线和线段的性质，熟练掌握各性质是解题的关键．
5．C
【分析】本题主要考查了完全平方式，根据完全平方公式进行判断即可掌握完全平方式是解题的关键．
【解答】解：选项A中，不符合完全平方式的特点，不是完全平方式，故选项A错误；
选项B中，不符合完全平方式的特点，不是完全平方式，故选项B错误；
选项C中，符合完全平方式的特点，是完全平方式，故选项C正确；
选项D中，不符合完全平方式的特点，不是完全平方式，故选项D错误；
故选：C．
6．A
【分析】运用同底数幂的除法进行分解，把值代入求职即可；
【解答】解：由题可得，
把，代入上式得：
原式．
故选：A．
【点拨】本题主要考查了同底数幂的除法，准确应用公式是解题的关键．
7．C
【分析】把a+b=10两边平方，利用完全平方公式化简，将ab=11代入求出a2+b2的值，代入原式计算即可得到结果．
【解答】解：把a+b=10两边平方得：
（a+b）2=a2+b2+2ab=100，
把ab=11代入得：
a2+b2=78，
∴原式=78-11=67，
故选：C．
【点拨】此题考查了完全平方公式的运用，熟练掌握完全平方公式的结构特征是解本题的关键．
8．D
【分析】观察图形，分别求出左右两边图形空白部分的面积，根据空白部分面积相等即可得出结论．
【解答】解：∵左边图形空白部分的面积，右边图形空白部分的面积，
∵空白部分面积相等，
∴，
故选：D．
【点拨】本题考查平方差公式的几何背景，结合图形得到空白部分的面积是解题的关键．
9．-36.
【分析】根据平方差公式解出即可.
【解答】.
故答案为:-36.
【点拨】本题考查平方差公式的运用,关键在于熟练掌握平方差运算.
10．##45度
【分析】本题考查余角与补角，解题的关键是根据互为余角的和等于，互为补角的和等于，用这个角表示出它的余角与补角，然后列方程求解即可．
【解答】解：设这个角是，则它的补角为，余角为，
根据题意得：，
解得：．
故答案为：．
11．9或-7
【分析】根据完全平方公式：，观察其构造，即可得出m的值.
【解答】解：
当时，；
当时，.
故答案为：9或-7.
【点拨】本题主要考查的是完全平方的公式，观察公式的构成是解题的关键.
12．9
【分析】根据平行线的性质和角平分线的定义得出BD=DE，EF=FC，进而解答即可．
【解答】∵DF∥BC，
∴∠DEB=∠EBC，∠FEC=∠ECB，
∵BE、CE分别是∠ABC和∠ACB的平分线，
∴∠DBE=∠EBC，∠FCE=∠ECB，
∴∠DBE=∠DEB，∠FEC=∠FCE，
∴BD=DE，EF=FC，
∴△ADF周长=AD+DF+AF=AD+AF+DE+EF=AD+AF+BD+FC=AB+AC=5+4=9，
故答案为：9．
【点拨】此题考查等腰三角形的性质，平行线的性质以及角平分线的性质，有效的进行线段的等量代换是正确解题的关键．
13．
【分析】此题考查多项式乘多项式，解题关键在于掌握多项式与多项式相乘的法则．
根据多项式与多项式相乘的法则计算，再根据对应项相等求得，，，，，，再代入计算即可求解．
【解答】∵
，
∴，，，，，，
∴．
故答案为：．
14．(1)
(2)
【分析】本题考查了负整数指数幂，零指数幂，整式的混合运算；
（1）根据零指数幂，负整数指数幂，有理数的乘方进行计算即可求解；
（2）根据多项式乘以单项式，多项式除以单项式，进行计算即可求解．
【解答】（1）解：
（2）解：
15．，12
【分析】根据平方差公式，完全平方公式及单项式除以单项式法则计算，再计算加减法，最后代入字母的值计算即可．
【解答】解：原式
．
把，代入，原式．
【点拨】此题考查了整式的化简求值，正确掌握平方差公式，完全平方公式及单项式除以单项式法则是解题的关键．
16．(1)40，图见解析
(2)10，40，144
(3)表见解析，小明被选中参加区知识竞赛的概率为
【分析】题目主要考查条形统计图与扇形统计图综合，用列表法或树状图法求概率等，理解题意，综合运用这些知识点是解题关键．
（1）根据D等级的频数及所占的百分比即可得出总的人数，然后乘以B等级所占的百分比即可得出B等级的人数，然后补全统计图即可；
（2）用A等级的频数除以总人数即可得出m的值；用度乘以C等级所占的比例即可；
（3）用列表法表示出所有等可能的结果，然后用概率公式求解即可．
【解答】（1）人，人，
故答案为：40，补全条形统计图如图所示：
（2），，
．
故答案为10，40，144；
（3）设除小明以外的三个人记作、、，从中任意选取2人，所有可能出现的情况如下：
共有12种等可能出现的情况，其中小明被选中的有6种，
所以小明被选中参加区知识竞赛的概率为．
17．见解析
【分析】根据平行线的判定可得AD∥BC，根据平行线的性质和等量关系可得∠4=∠BAC，再根据平行线的判定可得AB∥CD．
【解答】∵∠2=∠E（已知）
∴AD∥BC（ 内错角相等，两直线平行）
∴∠3=∠DAC（ 两直线平行，内错角相等）
∵∠3=∠4（已知）
∴∠4=∠DAC（ 等量关系）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF
即∠BAF=∠DAC
∴∠4=∠BAC（等量代换）
∴AB∥CD（ 同位角相等，两直线平行）
故答案为AD，内错角相等，两直线平行；DAC，两直线平行，内错角相等；DAC，等量关系；DAC，BAF；AB∥CD，同位角相等，两直线平行．
【点拨】本题考查了平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．
18．(1)，见解析
(2)
(3)，见解析
【分析】（1）根据角平分线的性质得到，得到，由此得到；
（2）过点E作，得，证得推出，由此得到，进而推出；
（3）由得，根据三角形内角和得，利用邻补角得，由此得到．
【解答】（1）．理由如下：
∵平分平分，
∴，
∵，
∴
∴．
（2），理由如下：
过点E作，
∴，

∵
∴
∴
∵
∴
∵
∴
∴；
（3）
证明：∵，
∴

∵
∴
∵
∴．
【点拨】此题考查了平行线的判定和性质，三角形的内角和定理，熟练掌握平行线的判定定理和性质定理是解题的关键．
19．20°或125°
【分析】根据两个角的两边分别垂直，画出图形，可得这两个角相等或互补，可设∠B是x度，利用方程即可解决问题．
【解答】解：设∠B是x度，则是(3x﹣40)度，根据题意得，
①如图1：∵∠AEC=∠BED，∠ACB=∠ADB=90°，
∴∠B＝∠A＝x，
∴x＝3x﹣40
解得，x＝20，
故∠A＝20°，
②如图2：延长DA交BC于点E，
∵∠BED+∠EAC=90°，∠BED+∠B=90°，
∴∠EAC=∠B
∴∠B+∠DAC＝180°，
∴x+3x﹣40＝180，
解得，x＝55，
3×55°﹣40°＝125°
故答案为：20°或125°．
【点拨】此题主要考查了垂线的性质和三角形内角和，解题关键是设未知数，根据题意画出图形，分类讨论，列出方程．
20．-16
【分析】将原多项式配方，变形为两个完全平方式减一个常数的形式，根据偶次方的非负性可求得答案．
【解答】4x2-12xy+10y2+4y-12
=4x2-12xy+9y2+y2+4y+4-16
=（2x-3y）2+（y+2）2-16
∵（2x-3y）2≥0，（y+2）2≥0
∴（2x-3y）2+（y+2）2-16≥-16
故答案为：-16．
【点拨】此题考查配方法的应用，偶次方的非负性，解题关键在于掌握运算法则.
21．
【分析】本题考查了对顶角的定义，熟记对顶角的概念是解题的关键．根据对顶角的概念即可求解．
【解答】解：若三条直线两两相交，最多有3个交点，对对顶角；
四条直线两两相交，最多有个交点，对对顶角；
，
条直线两两相交于不同的点时，可形成对对顶角；
故答案为：．
22．
【分析】本题考查了多项式的乘法，根据题意得出，进而根据多项式的乘法进行计算即可求解．
【解答】解：依题意，
即
∴
解得：，
∴这个多项式为：
故答案为：．
23．
【分析】本题主要考查数字的变化规律，解题的关键是根据已知数列得出．由已知数列得出规律，再依此计算出与，最后代入所求的代数式即可得出答案．
【解答】解：，，，，，
，
，，
，
故答案为：．
24．（1）；（2）；（3）2.
【分析】（1）依据变化规律，即可得到（x-1）（1+x+x2+x3+…+xn）=xn+1-1．
（2）依据（1）中的规律，即可得到1+2+22+23+24+…+22018的值；
（3）将314+315+…+3100进行变形然后运用①中的方法得到结果．
【解答】（1）观察总结规律，可得：原式=
（2）原式=(2-1)(1+2+22+23+24+…+22018)=
（3）
∵的个位数字以3,9,7,1进行四次一个循环，
∴的个位数字为3，的个位数字为9，
所以的个位数字为2.
【点拨】本题是数字类规律题，考查了整式乘法，认真观察、仔细思考，弄清题中的规律是解决这类问题的方法．
25．(1)各需付运费元，元；
(2)元；
(3)小华和小彤共需付运费元．
【分析】（）根据运费首重价格续重续重运费，结合续重以千克为计重单位(不足千克按千克计算)，即可求解；
（）根据运费首重价格续重续重运费，结合续重以千克为计重单位(不足千克按千克计算)，可用含的代数式表示出寄往市外及寄往市内所需运费，作差后即可求解；
（）设小彤所寄物品的重量为(为正整数，为小数部分)千克，则小华所寄物品的重量为千克，分和两种情况列方程求解即可；
本题考查了一元一次方程的应用、列代数式，运用分类讨论并根据题意列出方程是解题的关键．
【解答】（1）解：根据题意得，寄往市内一件千克的物品需付运费(元)；
寄往市外一件千克的物品需付运费(元)；
答：各需付运费元，元；
（2）解：根据题意得，寄往市内需付运费 元，
寄往市外需付运费 元，
∴元；
（3）解：设小彤所寄物品的重量为(为正整数，为小数部分)千克，则小华所寄物品的重量为千克，
当时，
小彤的运费为元，
小华的运费为元，
根据题意得，，
解得(不符合题意，舍去)；
当时，
小彤的运费为元，
小华的运费为元，
根据题意得，，
解得，
∴(元)，
答：小华和小彤共需付运费元．
26．(1)①；②
(2)当时，对应的定值为；当时，对应的定值为
【分析】（1）①根据题意并结合图形可得，代入数据计算即可；
②根据题意可得，，，继而得到关于的一元一次方程，求解即可；
（2）先找出临界值：当秒时，；当秒时，；当秒时，；当秒时，；当秒时，射线与射线重合，然后分四种情况讨论即可．
【解答】（1）解：①∵将射线绕着点逆时针旋转得到射线，
∴，
∵，
∴
，
∴的度数为；
②∵，，
∴，
∵，
∴，
解得：，
∴的值为；
（2）解：∵，射线从开始绕着点以每秒的速度逆时针旋转至结束，设旋转时间为，
则（秒），
当秒时，；
当时，（秒），
此时，
即当秒时，；
当时，（秒），
此时，
即当秒时，；
当时，（秒），
即当秒时，；
当秒时，射线与射线重合，
可分以下几种情况：
①当时，如图，
∵射线从开始绕着点以每秒的速度逆时针旋转，射线平分，射线绕着点逆时针旋转得到射线，，
∴，，，
∴，
∴
，
∴（定值）；
②当时，如图，
∵射线从开始绕着点以每秒的速度逆时针旋转，射线平分，射线绕着点逆时针旋转得到射线，，
∴，，，
∴，
，
∴（非定值）；
③当时，如图，
∵射线从开始绕着点以每秒的速度逆时针旋转，射线平分，射线绕着点逆时针旋转得到射线，，
∴，，，
∴，
，
∴，
∴（定值）；
④当时，如图，
∵射线从开始绕着点以每秒的速度逆时针旋转，射线平分，射线绕着点逆时针旋转得到射线，，
∴，，，
∴，
，
，
∴（非定值）；
综上所述，当时，对应的定值为；当时，对应的定值为．
【点拨】本题考查角的和差计算，角平分线的定义，平角的定义和周角的定义等知识点，运用了分类讨论的思想，本题难度较大．正确理解题意并运用分类讨论的思想是解题的关键．
寄往市内
寄往市外
首重
续重
首重
续重
元／千克
元／千克
元／千克
元／千克
说明：①每件快递按送达地（市内，市外）分别计算运费．
②运费计算方式：首重价格续重续重运费．首重均为千克，超过千克即要续重，续重以千克为计重单位（不足千克按千克计算）
一二
小明
小明
，小明
，小明
，小明
小明，
，
，
小明，
，
，
小明，
，
，