北京市陈经纶中学嘉铭分校2023-2024学年九年级下册月考数学试题（含解析）

这是一份北京市陈经纶中学嘉铭分校2023-2024学年九年级下册月考数学试题（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（每题2分，共16分）
1．南水北调工程在保障城市供水安全、增加首都水资源战略储备、改善居民生活用水条件、促进水资源涵养和恢复等方面，取得了重大的社会、经济、生态等综合效益．自2008年9月至2018年5月，北京已累计收水超过5 000 000 000立方米．将5 000 000 000用科学记数法表示为（ ）
A．0.5×1010B．5×1010C．5×109D．50×108
2．如图是某个几何体的三视图，该几何体是（ ）
A．圆锥B．四棱锥C．圆柱D．四棱柱
3．如图，△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠1=35°，则∠B的度数为（ ）
A．25°B．35°C．55°D．65°
4．实数a，b，c在数轴上的对应点的位置如图所示．下列式子正确的是（ ）
A．B．C．D．
5．已知反比例函数的表达式为，它的图象在各自象限内具有y随x增大而减小的特点，那么k的取值范围是
A．k＞1B．k＜1C．k＞0D．k＜0
6．如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD=1，BD=2，则的值为（ ）
A．B．C．D．
7．如图，在⊙O中，直径AB与弦CD垂直相交于点E，连结AC，OC，若∠A=30°，OC=4，则弦CD的长是（ ）
A．B．4C．D．8
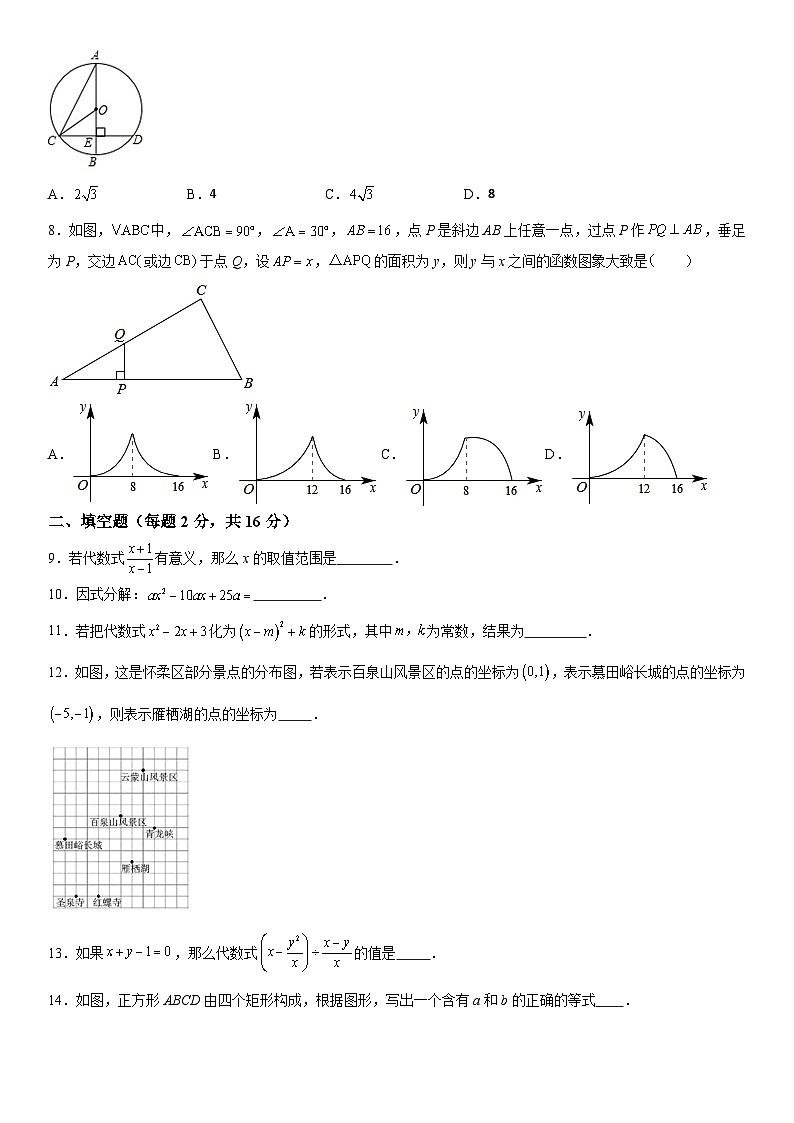
8．如图，中，，，，点P是斜边AB上任意一点，过点P作，垂足为P，交边或边于点Q，设，的面积为y，则y与x之间的函数图象大致是
A．B．C．D．
二、填空题（每题2分，共16分）
9．若代数式有意义，那么x的取值范围是 ．
10．因式分解： ．
11．若把代数式化为的形式，其中为常数，结果为 ．
12．如图，这是怀柔区部分景点的分布图，若表示百泉山风景区的点的坐标为，表示慕田峪长城的点的坐标为，则表示雁栖湖的点的坐标为 ．
13．如果，那么代数式的值是 ．
14．如图，正方形ABCD由四个矩形构成，根据图形，写出一个含有a和b的正确的等式 ．
15．学习了三角形的有关内容后，张老师请同学们交流这样一个问题：“已知一个等腰三角形的周长是12，其中一条边长为3，求另两条边的长”．同学们经过片刻思考和交流后，小明同学举手讲：“另两条边长为3、6或4.5、4.5”，你认为小明回答是否正确： ，理由是 ．
16．某商场在端午节前以1元/个的价格购进1000个粽子，现有以下三种销售方式：不加工直接卖，对产品进行粗加工后再卖，对产品进行精加工后再卖．受加工能力和气温影响，粗加工一天只能加工200个，细加工一天只能加工100个，两种加工不能同时进行，且最多加工三天．
假设所有粽子均能全部售出，则以下销售方式中利润最大的是 ．
方案一：不加工直接销售；
方案二：三天全部进行精加工，剩下的直接卖；
方案三：两天精加工，一天粗加工，剩下的直接卖；
方案四：两天粗加工，一天精加工，剩下的直接卖．
三、解答题（12道题，共68分）
17．计算：．
18．解不等式组：
19．已知，求代数式的值．
20．列方程解应用题
某学校组织学生到离校千米的国家博物馆进行实践教育活动，同学们统一从学校乘车前往．小明在去学校的途中遇上堵车，比同学们晚分钟从学校出发，由他的家长开车沿相同路线送小明赶往国家博物馆，结果小明和同学们同时到达．已知小明的速度是同学们的速度的2倍，求同学们的速度是每小时多少千米？
21．已知：关于x的方程有实数根．
（1）求m的取值范围；
（2）若方程的根为有理数，求正整数m的值．
22．如图，菱形ABCD的对角线AC和BD交于点O，分别过点C、D作CE∥BD，DE∥AC，CE和DE交于点E.
（1）求证：四边形ODEC是矩形；
（2）当∠ADB=60°，AD=时，求tan∠EAD的值.
23．如图，中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E.过D作DF⊥AC，垂足为F.
（1）求证：DF是⊙O的切线
（2）若CD=3，CE=，求⊙O的半径.
24．已知：在平面直角坐标系xOy中，点A（-1，2）在函数(x<0)的图象上．

（1）求m的值；
（2）过点A作y轴的平行线，直线与直线交于点B，与函数(x<0)的图象交于点C，与轴交于点D．
①当点C是线段BD的中点时，求b的值；
②当BC25．如图，AB = 6cm，∠CAB = 25°，P是线段AB上一动点，过点P作PM⊥AB交射线AC于点M，连接MB，过点P作PN⊥MB于点N．设A，P两点间的距离为xcm，P，N两点间的距离为ycm．（当点P与点A或点B重合时，y的值均为0）小海根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小海的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
（说明：补全表格时相关数值保留两位小数）（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：当y=0.5时，与之对应的值的个数是 .
26．在平面直角坐标系xOy中，点A（x1，y1），B（x2，y2）在抛物线y＝﹣x2+（2a﹣2）x﹣a2+2a上，其中x1＜x2．
(1)求抛物线的对称轴（用含a的式子表示）；
(2)①当x＝a时，求y的值；
②若y1＝y2＝0，求x1的值（用含a的式子表示）．
(3)若对于x1+x2＜﹣4，都有y1＜y2，求a的取值范围．
27．已知，点是边上一动点（不与A，B重合）分别过点A，B向直线作垂线，垂足分别为E，F，Q为边的中点．
(1)如图1，当点P与点Q重合时，与的数量关系是_________；
(2)如图2，当点P在线段上不与点Q重合时，试判断与的数量关系是_________；
(3)如图3，当点P在线段的延长线上时，此时（2）中的结论是否成立？请画出图形并给予证明．
28．在平面直角坐标系xOy中，A，B两点的坐标分别为A（2，2），B（2，﹣2）．对于给定的线段AB及点P，Q，给出如下定义：若点Q关于AB所在直线的对称点Q′落在△ABP的内部（不含边界），则称点Q是点P关于线段AB的内称点．
（1）已知点P（4，﹣1）．
①在Q1（1，﹣1），Q2（1，1）两点中，是点P关于线段AB的内称点的是 ；
②若点M在直线y＝x﹣1上，且点M是点P关于线段AB的内称点，求点M的横坐标xM的取值范围；
（2）已知点C（3，3），⊙C的半径为r，点D（4，0），若点E是点D关于线段AB的内称点，且满足直线DE与⊙C相切，求半径r的取值范围．
参考答案与解析
1．C
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】5 000 000 000=5×109，
故选C．
【点拨】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
2．B
【分析】由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状
【解答】解：根据主视图和左视图为矩形判断出是柱体，根据俯视图是长方形可判断出这个几何体应该是四棱柱．
故选B.
【点拨】本题考查了由三视图找到几何体图形,属于简单题,熟悉三视图概念是解题关键.
3．C
【解答】试题分析：∵DE∥BC，∴∠C=∠1=35°，∵∠A=90°，∴∠B=90°－∠C=90°－35°=55°．故选C．
考点：1．平行线的性质；2．直角三角形的性质．
4．B
【分析】根据数轴上的点表示的数右边的总比左边的大，有理数的运算，绝对值的意义，可得答案．
【解答】由数轴可知 ，，0＜c＜1
∴，故A错误，
，故B正确，
，故C错误，
，故D错误．
故本题选B．
【点拨】本题考查了实数与数轴，利用数轴上的点表示的数右边的总比左边的大，有理数的运算，绝对值的意义等，熟练掌握是解题的关键．
5．A
【解答】试题分析：因为反比例函数的图象在各自象限内具有y随x增大而减小，所以k-1＞0，所以k＞1，故选A.
考点：反比例函数的性质.
6．B
【解答】试题分析：∵DE∥BC，∴，∵，∴．故选B．
考点：平行线分线段成比例．
7．C
【解答】试题分析：因为CE=DE，AB是⊙O的直径，所以CD AB,又∠A=30°，OA=OC=4,所以∠COE=60°，所以在Rt△COE中，CE=OCsin60°=4×=2，所以CD=2CE=,故选C.
考点：1.垂径定理的推论；2.直角三角形的性质；3.锐角三角函数.
8．D
【分析】首先过点C作CD⊥AB于点D，由△ABC中，∠ACB=90°，∠A=30°，可求得∠B的度数与AD的长，再分别从当0≤≤12时与当12＜x≤16时，去分析求解即可求得答案．
【解答】解：∵∠ACB=90°，∠A=30°，AB=16，
∴∠B=60°，BC=AB=8，
∴∠BCD=30°，
∴BD=BC=4，
∴AD=AB﹣BD=12．
如图1，当0≤AD≤12时，
AP=x，PQ=AP•tan30°=x，
∴y=x•x=x2；
如图2：当12＜x≤16时，BP=AB﹣AP=16﹣x，
∴PQ=BP•tan60°=（16﹣x），
∴y=x•（16﹣x）=，
该函数图象前半部分是抛物线开口向上，后半部分也为抛物线开口向下，
故选D．
【点拨】本题考查了动点问题的函数图象，运用分类讨论思想、结合图形进行解题是关键.
9．
【分析】要使分式有意义，分式的分母不能为0．依此可得，求解即可．
【解答】分式有意义，则，所以．
故答案为：．
【点拨】本题考查了分式有意义的条件，解此类问题，只要令分式中分母不等于0，求得x的值即可．
10．
【分析】先提因式a，再运用完全平方公式分解即可．
【解答】
故答案为：．
【点拨】本题主要考查了提公因式法和运用公式法分解因式，先提公因式，再用公式分解因式是解题的关键．注意：因式分解要分解到不能再分解为止．
11．
【分析】本题主要考查了配方法的意义，根据题意利用配方法求解即可．
【解答】解：
，
故答案为：．
12．
【分析】直接利用已知点坐标得出原点位置，进而得出答案．
【解答】
解：如图所示：雁栖湖的点的坐标为：（1，-3）．
故答案为（1，-3）．
【点拨】本题考查坐标确定位置，正确得出原点的位置是解题关键．
13．1
【分析】本题考查了分式的混合运算,对所求代数式根据分式的混合运算顺序进行化简，再把变形后整体代入即可，解题的关键是掌握运算顺序并运用整体代入法计算．
【解答】解：


，
，
，
即原式，
故答案为：1．
14．（a+b）2＝a2+2ab+b2．
【分析】根据正方形ABCD的面积等于四个小矩形的面积之和写出即可．
【解答】等式为：（a+b）2＝a2+2ab+b2．
故答案为（a+b）2＝a2+2ab+b2．
【点拨】本题考查对完全平方公式几何意义的理解，应从整体和部分两方面来理解完全平方公式的几何意义；主要围绕图形面积展开分析．
15． 不正确 3，3，6不能组成三角形
【分析】本题分成两种情况，当3为底边时或当3为腰时，分情况讨论即可．
【解答】解：当3为底边时，另两边为4.5、4.5，
当3为腰时，另两边为3、6，但是3+3=6，所以不能组成三角形，所以另两边只能为4.5、4.5，
故小明回答不正确，理由是3，3，6不能组成三角形，
故答案为：不正确；3，3，6不能组成三角形．
【点拨】本题考查，等腰三角形的性质，三角形的三边关系，能够熟练应用等腰三角形的性质是解决本题的关键．
16．方案四
【分析】分别计算出几种方案的利润，选择利润最大的方案即可．
【解答】方案一利润： （元）；
方案二利润： （元）；
方案三利润：（元）；
方案四利润：（元）；
故应该选择方案四利润最大，
故答案为：方案三．
【点拨】本题主要考查了有理数的加减乘除混合运算，正确理解题意，列出式子进行计算是解题的关键．
17．5
【解答】试题分析：先将各式的值化简，然后按照实数的运算法则计算即可.
试题解析：解：原式= 4分（每个1分）
=. 5分
考点：实数的计算.
18．
【分析】求出每个不等式的解集，再求出解集的公共部分即可．
【解答】由解得，；
由解得，．
∴原不等式组的解集为：．
【点拨】本题考查了解一元一次不等式组，求出不等式组中每一个不等式的解集是关键，常常利用口诀求出这些解集的公共部分：同大取大，同小取小，大小小大中间找，大大小小解不了（无解）．
19．9．
【解答】试题分析：原式第一项利用完全平方公式展开，第二项利用平方差公式化简，最后一项利用单项式乘以多项式法则计算，去括号合并得到最简结果，将已知等式变形代入代入计算即可求出值．
试题解析：原式==，
当，即时，原式=1+8=9．
考点：整式的混合运算—化简求值．
20．40千米/时
【分析】本题主要考查了分式方程的实际应用，设同学们的速度为千米/时．则小明的速度为千米/时，根据小明花费的时间比同学们的时间少15分钟列出方程求解即可．
【解答】解：设同学们的速度为千米/时．则小明的速度为千米/时，15分钟小时．
依题意，列方程得，
解得．
经检验是所列方程的解，并且符合题意．
答：同学们的速度为40千米/时．
21．（1）≤4且；（2）m=3或m=4．
【分析】（1）根据一元二次方程根的判别式结合题意即可求解；
（2）根据（1）的结论可求出m的取值，然后根据△为平方数即可求出m的值．
【解答】（1）一元二次方程，
，，，
，
∵原方程有实数根，
∴≥0，
解得：≤4，
∴m的取值范围是≤4且；
（2）∵m为正整数，
∴m可取1，2，3，4．
当m=1时，，不是平方数，方程不是有理根；
当m=2时，，不是平方数，方程不是有理根；
当m=3时，，是平方数，方程为有理根；
当m=4时，，是平方数，方程为有理根；
∵方程为有理根，
∴m=3或m=4时，方程为有理根．
【点拨】本题主要考查了一元二次方程根的判别式，熟知一元二次方程（a≠0）的根与△的关系是解答此题的关键．
22．（1）见解析（2）
【分析】（1）先根据条件CE∥BD，DE∥AC，证明四边形ODEC是平行四边形，然后再证明∠DOC=90°即可；（2）过点E作EF⊥AD，交AD的延长线于F，首先将∠EAD转化为Rt△AEF的内角，然后在Rt△DEF中，利用三角函数求出EF，DF的长，最后根据三角函数的定义可求出tan∠EAD的值.
【解答】（1）证明：∵ CE∥BD，DE∥AC，
∴ 四边形ODEC是平行四边形.
又 ∵菱形ABCD，
∴ AC⊥BD，∴ ∠DOC=90°.
∴ 四边形ODEC是矩形.
（2）如图，过点E作EF⊥AD，交AD的延长线于F.
∵ AC⊥BD，∠ADB=60°，AD=，
∴ OD=，AO=OC=3.
∵ 四边形ODEC是矩形，
∴ DE=OC=3，∠ODE=90°.
又∵ ∠ADO+∠ODE +∠EDF=180°，
∴ ∠EDF=30°.
在Rt△DEF中，∠F=90°，∠EDF=30°.
∴ EF=.
∴ DF=.
在Rt△AFE中，∠DFE=90°，
∴tan∠EAD=.
考点：1.菱形的性质；2.矩形的判定与性质；3.锐角三角函数..
23．（1）见解析；（2）⊙O的半径为.
【分析】（1）连结AD,连结OD.根据圆的基本性质知，∠ADB=90°，结合题意知，OD是△BCA的中位线，所以OD∥AC，再根据题意及切线性质，进行作答.（2）连结DE，则BE⊥AC.根据题意及（1）中结论，得到 △DCF∽△ACD，再根据相似三角形性质得，AC的值，即AB的值，最后得到⊙O的半径.
【解答】(1)证明：连结AD,连结OD.
∵以AB为直径的⊙O交BC于点D
∴∠ADB=90°
∵AB=AC
∴BD=DC
又∵O是AB中点
∴OD是△BCA的中位线
∴OD∥AC
∵DF⊥AC
∴DF⊥OD
∴DF是⊙O的切线；
（2）连结DE，则BE⊥AC.
∵DF⊥AC, BE⊥AC
∴DF∥BE
∵BD=CD
∴EF=CF
∵CE=
∴CF=
∵∠ADC=∠DFC= 90°, ∠DCF=∠DCA
∴△DCF∽△ACD
∴
∵CD=3,CF=
∴AC=5
∵AB=AC
∴AB=5
∴⊙O的半径为.
【点拨】本题考查了圆的基本性质、与直线与圆的位置关系、相似三角形的性质的综合运用，熟练掌握圆的基本性质、与直线与圆的位置关系、相似三角形的性质的综合运用是本题解题关键.
24．（1）m= -2；（2）①b=3；②b> -3．
【分析】（1）把A（-1，2）代入解析式即可求解；
（2）①根据题意知点B的横坐标为-1，点D的横坐标为0，由于点C是BD的中点，利用中点坐标公式即可求得点C的横坐标，代入中可求得点C的坐标，代入函数 中，即可求解；
②先利用①的方法求得BC=BD即点B是CD的中点时的值，观察图象，即可求得b的取值范围．
【解答】（1）把A（-1，2）代入函数(x<0)中，
∴ ；
（2）① 如图，
根据题意知：点B的横坐标为-1，点D的横坐标为0，

∵点C是BD的中点，
∴点C的横坐标为，
把代入函数中，得y = 4，
∴点C的坐标为（，4），
把点C的坐标为（，4）代入函数 中，
得：，
解得：；
② 当点B是CD的中点时，BC=BD，

此时，点B的横坐标为-1，点D的横坐标为0，
设点C的横坐标为，
∴，
解得：，
把代入函数中，得y = 1，
∴点C的坐标为（，1），
把点C的坐标为（，1）代入函数 中，
得：，
解得：；
观察图象，当时，BCBD，
故答案为：．
【点拨】本题考查了待定系数法求一次函数和反比例函数的解析式，一次函数与反比例函数图象交点情况，中点坐标公式的应用，解题关键是正确读图、识图、观察图象，利用数形结合思想解决问题．
25．解：（1）0.91（答案不唯一）；（2）作图见解析；（3）两个.
【解答】试题分析：（1）利用取点，测量的方法，即可解决问题；
（2）利用描点法，画出函数图象即可；
（3）做出直线y=0.5，由图像可知有两个．
解：（1）（答案不唯一）
（2）如图，
（3）由图像可知，当y=0.5时，与之对应的值的个数是两个.
26．(1)对称轴为直线x＝a﹣1
(2)①y=0；②x1＝a﹣2
(3)a≥﹣1
【分析】（1）根据抛物线的对称轴x＝﹣求解即可；
（2）①将x＝a代入y＝﹣x2+（2a﹣2）x﹣a2+2a求解即可；②若y1＝y2＝0，则﹣x2+（2a﹣2）x﹣a2+2a＝0，解方程并根据x1＜x2，求出x1的值．
（3）由题意得出x1＜﹣2，则只需讨论x1＜a﹣1的情况，分两种情况：①当a≥﹣1时，又有两种情况：x1＜x2＜a﹣1，x1＜a﹣1＜x2，分别结合二次函数的性质及x1+x2＜﹣4计算即可；②当a＜﹣1时，令x1＝a﹣1，x2＝﹣2，此时x1+x2＜﹣4，但y1＞y2，不符合题意．
【解答】（1）解：抛物线的对称轴为直线x＝﹣＝a﹣1；
（2）解：①当x＝a时，y＝﹣a2+（2a﹣2）a﹣a2+2a
＝﹣a2+2a2﹣2a﹣a2+2a
＝0；
②当y1＝y2＝0时，﹣x2+（2a﹣2）x﹣a2+2a＝0，
∴x2﹣（2a﹣2）x+a2﹣2a＝0，
∴（x﹣a+2）（x﹣a）＝0，
∵x1＜x2，
∴x1＝a﹣2；
（3）
解：①当a≥﹣1时，
∵x1＜x2，x1+x2＜﹣4，
∴x1＜﹣2，只需讨论x1＜a﹣1的情况．
若x1＜x2＜a﹣1，
∵x＜a﹣1时，y随着x的增大而增大，
∴y1＜y2，符合题意；
若x1＜a﹣1＜x2，
∵a﹣1≥﹣2，
∴2（a﹣1）≥﹣4，
∵x1+x2＜﹣4，
∴x1+x2＜2（a﹣1）．
∴x1＜2（a﹣1）﹣x2．
∵x＝2（a﹣1）﹣x2时，y1＝y2，x＜a﹣1时，y随着x的增大而增大，
∴y1＜y2，符合题意．
②当a＜﹣1时，令x1＝a﹣1，x2＝﹣2，此时x1+x2＜﹣4，但y1＞y2，不符合题意；
综上所述，a的取值范围是a≥﹣1．
【点拨】本题属于二次函数的综合题，涉及二次函数的性质、求函数值、运用二次函数求不等式等知识点，灵活运用二次函数的性质成为解答本题的关键．
27．(1)
(2)
(3)成立，见解析
【分析】本题考查了全等三角形的性质和判定，直角三角形斜边上中线性质的应用．
（1）由，，可知，结合为中点，可证，即可证得，即可得答案；
（2）延长交延长线于，证，推出，根据直角三角形斜边上中线性质求出即可；
（3）延长、交于，证，推出，根据直角三角形斜边上中线性质求出即可．
【解答】（1）解：∵为中点，
∴，
∵，，
∴，
在和中，
，
∴，
∴，
故答案为：．
（2）解：，理由如下：
如图，延长交延长线于，
∵为中点，
∴，
∵，，
∴，
∴，
又∵，
∴，
∴，
∵，
∴是斜边上的中线，
∴，
即．
（3）（2）中的结论仍然成立，
证明：如图，
延长、交于，
∵，，
，
，
在和中，
，
，
，
，
是斜边上的中线，
．
28．（1）①Q1；②0＜xM＜2，（2）＜r≤．
【分析】（1）①利用内对称点的意义即可得出结论；
②先判断出点O关于直线AB的对称点P'在直线y＝x﹣1上，即可判断出结论；
（2）判断出DE与圆C相切时，圆C最大的半径和最小的位置，计算即可得出结论．
【解答】解：（1）①
作出图形，由内对称点的意义得，点P关于线段AB的内称点的是Q1，
故答案为Q1；
②如图2，
点P（4，﹣1）关于AB所在直线的对称点P'（0，﹣1），此时，点P'恰好在直线y＝x﹣1上，
∵点M是点P关于线段AB的内对称点，
∴点M关于AB所在直线的对称点M'落在△ABP内部（不含边界），
∵点M在直线y＝x﹣1上，
∴点M应在线段P'G上（点G为线段AB与直线y＝x﹣1的交点），且不与两个端点P'，G重合，
∴0＜xM＜2，
（2）如图3，
∵点E是点D关于线段AB的内称点，
∴点E关于AB所在直线的对称点E'应在△ABD内部（不含边界），
∵点D关于AB所在直线的对称点为原点O，
∴点E应在△ABO的内部（不含边界），
∵A（2，2），C（3，3），D（4，0），
∴AC＝，AD＝2，CD＝，
∴AC2+AD2＝CD2，
∴∠CAD＝90°，
∴AC⊥AD，
此时，直线DA与以AC为半径的⊙C相切，半径AC＝，
当直线DE与以CD为半径的⊙C相切，点D为切点，⊙C的半径最大，最大值为，
∴符合题意的⊙C的半径r的取值范围是＜r≤．
【点拨】此题是一次函数综合题，主要考查了点的对称点的坐标的确定，理解和掌握新定义是解本题的关键．
加工方式
加工成本
销售单位
售价
直接卖
0
个
2元/个
粗加工
1元/个
包装袋（一袋5个）
30元/袋
精加工
2.5元/个
礼盒（一盒10个）
85元/盒
x/cm
0.00
0.60
1.00
1.51
2.00
2.75
3.00
3.50
4.00
4.29
4.90
5.50
6.00
y/cm
0.00
0.29
0.47
0.70
1.20
1.27
1.37
1.36
1.30
1.00
0.49
0.00