福建省建瓯市芝华中学2023-2024学年七年级下册第一次月考数学试题（含解析）

这是一份福建省建瓯市芝华中学2023-2024学年七年级下册第一次月考数学试题（含解析），共16页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
数学试卷
(考试范围：第5-6章 考试时长：120分钟 满分：150分)
一、单选题本题共10小题，每小题4分，共40分．在每个小题给出的四个选项中，只有一项是符合要求的．
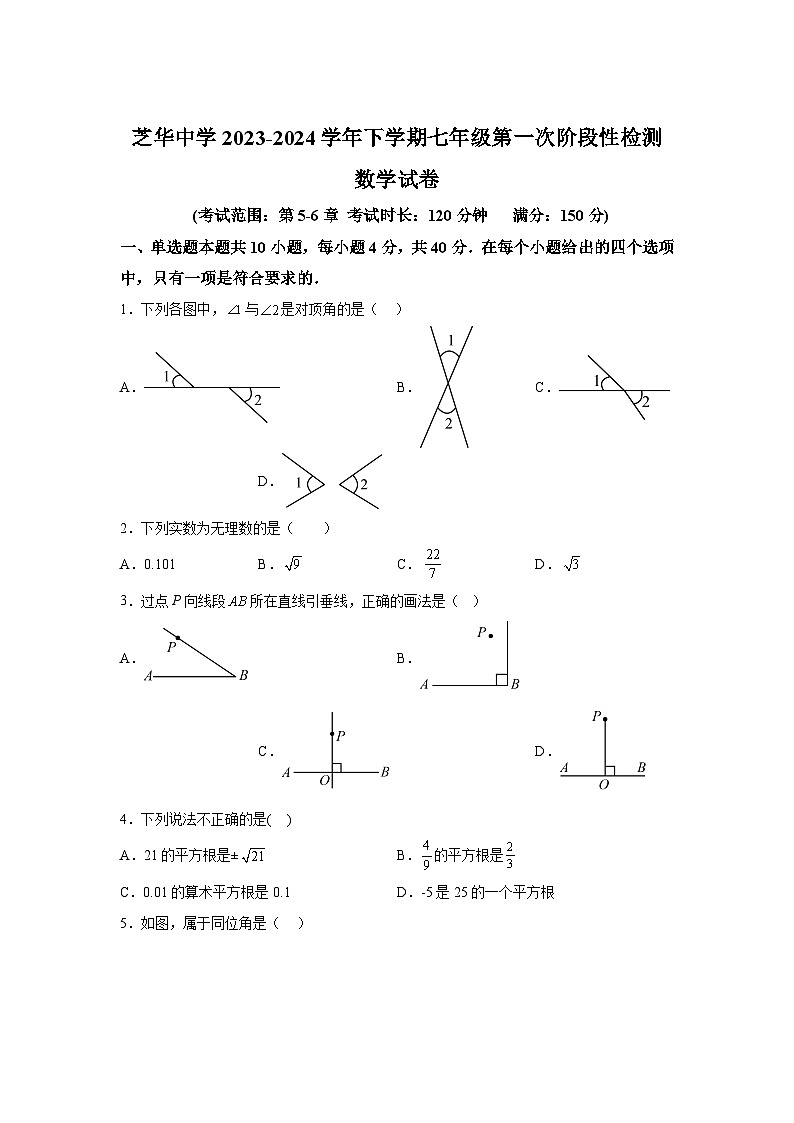
1．下列各图中，与是对顶角的是（ ）
A． B． C． D．
2．下列实数为无理数的是（ ）
A．0.101B．C．D．
3．过点P向线段所在直线引垂线，正确的画法是（ ）
A． B． C． D．
4．下列说法不正确的是( )
A．21的平方根是±B．的平方根是
C．0.01的算术平方根是0.1D．-5是25的一个平方根
5．如图，属于同位角是（ ）

A．和B．和C．和D．和
6．如图，沿BC所在直线向右平移得到，已知，则的长为（ ）

A．B．C．D．
7．如图，已知点O在直线AB上，CO⊥DO于点O，若∠1=145°，则∠3的度数为（ ）
A．35°B．45° C．55°D．65°
8．已知，，且，则的值为（ ）
A．2或12B．2或C．或12D．或
9．如图，已知，若，则（ ）
A．B．C．D．
10．一列数则 （ ）
A．B．C．D．
二、填空题(本题共6小题，每小题4分，共24分)
11．的立方根是 ．
12．请将命题“邻补角互补”写成“如果……那么……”的形式： ．
13．比较大小： 0.5（填“＞”“＜”或“＝”）．
14．如图，已知，，则 度.
15．若=2.938，=6.329，则= ．
16．如图，已知，，，和的平分线交于，和的平分线交于，和的平分线交于，按如此方式继续下去，用，的代数式表示的度数为 ．

三、解答题(本题共7小题，共86分．解答应写出文字说明、证明过程或演算步骤)
17．计算：
（1）；
（2）．
18．解方程
(1)；
(2)．
19．在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示．
（1）现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．请画出平移后的△A′B′C′；
（2）线段BC与B′C′的关系是 ；
（3）△A′B′C′的面积为 ．
20．如图，点E、F分别在、上，于点，，，求证：．请完善解答过程，并在括号内填写相应的依据．
证明：∵（已知），
∴∠（ ），
又∵（已知），
∴ （同位角相等，两直线平行），
∴ （ ）
又∵（平角的定义）
∴ 90°，
又∵（已知）
∴（ ）
∴（ ）．
21．已知一个正数的两个平方根是m+3和2m﹣15．
(1)求这个正数是多少？
(2)的平方根又是多少？
22．已知点O为直线上一点，作，且满足，

(1)如图1，求的度数；
(2)如图2，作平分，求的度数；
(3)在（2）的条件下，作，求的度数
23．已知，AB∥CD，点E在CD上，点G，F在AB上，点H在AB，CD之间，连接FE，EH，HG，∠AGH＝∠FED，FE⊥HE，垂足为E．
（1）如图1，求证：HG⊥HE；
（2）如图2，GM平分∠HGB，EM平分∠HED，GM，EM交于点M，求证：∠GHE＝2∠GME；

（3）如图3，在（2）的条件下，FK平分∠AFE交CD于点K，若∠KFE：∠MGH＝13：5，求∠HED的度数．

参考答案与解析
1．B
【分析】根据对顶角的定义即可进行解答．
【解答】解：根据题意可得：
与是对顶角的是
“ ”，
故选：B．
【点拨】本题主要考查了对顶角的定义，解题的关键是掌握如果一个角的两边分别是另一个角两边的反向延长线，且这两个角有公共顶点，那么这两个角是对顶角．
2．D
【分析】根据无限不循环小数叫做无理数，进行判断即可．
【解答】解：在0.101，，，中，是无理数的是；
故选D．
3．C
【分析】根据过直线外一点作已知直线的垂线的作法判断即可．
【解答】A选项，没有垂直，故该选项不符合题意；
B选项，没有过点P，，故该选项不符合题意；
C选项，过点P作的垂线，垂线是直线，故该选项符合题意；
D选项，为垂线段，不是直线，故该选项不符合题意；
故选：C．
【点拨】本题考查了垂线，掌握当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直是解题的关键．
4．B
【解答】解：A、21的平方根是，故此项选正确；
B、的平方根是，故此选项错误；
C、0.01的算术平方根是0.1，故此选项正确；
D、－5是25的一个平方根，故此选项正确．
故选：B．
【点拨】本题考查了平方根的概念和表示方法，熟记平方根的概念是解决此题的关键，注意正数的平方根有两个，它们互为相反数．
5．C
【分析】根据同位角的定义：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．进行判断即可．
【解答】解：由图可知，和是同位角；
故选：C．
【点拨】本题考查的是同位角的定义，掌握两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角是同位角是解题的关键．
6．A
【分析】首先根据平移的性质得到，进而求解即可．
【解答】∵沿BC所在直线向右平移得到，
∴，
∴．
故选：A．
【点拨】本题考查平移的性质，经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等，解题关键是要找到平移的对应点．
7．C
【解答】试题分析：∵∠1=145°，∴∠2=180°-145°=35°，
∵CO⊥DO，∴∠COD=90°，
∴∠3=90°-∠2=90°-35°=55°；
故选C．
考点：垂线．
8．D
【解答】根据=5，=7，得，因为，则，则=5-7=-2或-5-7=-12.
故选D.
9．A
【分析】由题意可判定，根据两直线平行，同旁内角互补，即可得出的度数．
【解答】解：∵，
∴，
∴，
又∵，
∴，
∴．
故选：．
【点拨】本题主要考查了平行线的判定与性质，熟练掌握相关知识是解题关键．
10．B
【分析】本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，求出所求式子的值．根据题意，可以写出这列数的前几个数，然后即可发现数字的变化特点，从而可以求得所求式子的值．
【解答】解：由题意可得，
，
，
，
，
，
故上面的数据以，，2为一个循环，依次出现，
∵，，
∴
故选：B．
11．-2
【分析】根据立方根的定义进行求解即可得．
【解答】解：∵（﹣2）3=﹣8，
∴﹣8的立方根是﹣2，
故答案为﹣2．
【点拨】本题考查了立方根的定义，熟练掌握立方根的定义是解题的关键．
12．如果两个角是邻补角，那么这两个角互补
【分析】根据题意，分清命题的条件和结论，即可．
【解答】命题“邻补角互补”写成“如果……那么……”的形式为：如果两个角是邻补角，那么这两个角互补．
故答案为：如果两个角是邻补角，那么这两个角互补．
【点拨】本题考查命题的定义，解题的关键是理解命题的条件和结论．
13．>
【分析】本题考查了无理数的估算，先得出，把，再比较与，即可作答．
【解答】解：∵，
∴
则
故答案为：>
14．102°
【分析】先根据∠1=∠2得出AD∥BC，再由平行线的性质即可得出结论．
【解答】解：∵∠1=∠2，
∴AD∥BC．
∴∠D+∠BCD=180°
∵∠D=78°，
∴∠BCD=180°-78°=102°．
故答案为：102°．
【点拨】本题考查的是平行线的判定与性质，先根据题意判断出AD∥BC是解答此题的关键．
15．293.8
【分析】将变形为=×100, 再代入计算即可求解．
【解答】解：
=
=×100
=293.8.
故答案为293.8．
【点拨】考查了立方根，关键是将变形为.
16．
【分析】根据平行线的性质得，，再根据角平分线的定义得，，然后利用三角形内角和定理得到，即，则，同理得，，再利用前面的结论可得到．
【解答】解：，，，
，，
和的平分线交于，
，
，即，
，
和的平分线交于，
，，
，即，
，
同理得，
．
故答案为．
【点拨】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．解决本题的关键是熟练掌握平行线的性质，也考查了三角形内角和定理．
17．（1）；（2）0
【分析】（1）根据算术平方根的定义、立方根的定义和绝对值的性质计算即可；
（2）根据立方根的定义、算术平方根的定义和乘方的性质计算即可．
【解答】解：（1）
（2）
【点拨】此题考查的是实数的混合运算，掌握算术平方根的定义、立方根的定义、绝对值的性质和乘方的性质是解决此题的关键．
18．(1)
(2)
【分析】本题考查了利用平方根、立方根求解方程，正确掌握相关性质内容是解题的关键．
（1）先把等式两边同时除以2，再利用平方根的性质，解出的值，即可作答；
（2）先把等式两边同时除以3，再利用立方根的性质，解出的值，即可作答．
【解答】（1）解：
∴
∴
∴；
（2）解：
∴

．
19．（1）见解析；（2）平行且相等；（3）
【分析】（1）利用点A和A′的位置确定平移的方向与距离，然后利用此平移规律画出B、C的对应点B′、C′即可；
（2）根据平移的性质进行判断；
（3）用一个矩形的面积分别减去三个三角形的面积计算△A′B′C′的面积．
【解答】解：（1）如图，△A′B′C′为所作；
（2）线段BC与B′C′的关系是平行且相等；
故答案为：平行且相等；
（3）△A′B′C′的面积＝3×3﹣×1×2﹣×2×3﹣×3×1＝．
故答案为：．
【点拨】本题考查了作图-平移变换：确定平移后图形的基本要素有两个：平移方向、平移距离．作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
20．见解析
【分析】此题主要考查了平行线的判定和性质．由垂直的定义得到，由平行线的性质得到，由平角定义得到，由余角的性质得到，即可证明．
【解答】证明：∵（已知），
∴（垂直的定义），
又∵（已知），
∴ （同位角相等，两直线平行），
∴（两直线平行，同位角相等）
又∵（平角的定义）
∴°，
又∵（已知）
∴（同角的余角相等）
∴．（内错角相等，两直线平行）
21．（1）49；（2）±.
【分析】（1）根据一个正数的平方根有两个，它们互为相反数即可解得m的值；
（2）利用（1）的结果平方根的定义即可求解.
【解答】解：（1）∵m+3和2m﹣15是同一个正数的平方根，则这两个数互为相反数．
即：（m+3）+（2m﹣15）=0
解得m=4．
则这个正数是（m+3）2=49．
（2）=3，则它的平方根是±．
【点拨】题目主要考查平方根的的性质及相反数的定义，一元一次方程的解法，理解平方根的性质与求法是解题关键．
22．(1)
(2)
(3)的度数是或
【分析】（1）根据，，即可求解；
（2）先求出，再由平分，可得，即可求解；
（3）分两种情况讨论：当在直线上方时，当在直线下方时，即可求解．
【解答】（1）解：，
；
（2）解：，
，
又平分，
，
；
（3）解：当在直线上方时，
，
，
，
，
当在直线下方时，
，
，
又
，
；
综上的度数是或．
【点拨】本题主要考查了余角，有关角平分线的计算，注意分类讨论思想的运用以及数形结合思想的运用．
23．（1）见解析；（2）见解析；（3）40°
【分析】（1）根据平行线的性质和判定解答即可；
（2）过点H作HP∥AB，根据平行线的性质解答即可；
（3）过点H作HP∥AB，根据平行线的性质解答即可．
【解答】证明：（1）∵AB∥CD，
∴∠AFE＝∠FED，
∵∠AGH＝∠FED，
∴∠AFE＝∠AGH，
∴EF∥GH，
∴∠FEH+∠H＝180°，
∵FE⊥HE，
∴∠FEH＝90°，
∴∠H＝180°﹣∠FEH＝90°，
∴HG⊥HE；
（2）过点M作MQ∥AB，

∵AB∥CD，
∴MQ∥CD，
过点H作HP∥AB，
∵AB∥CD，
∴HP∥CD，
∵GM平分∠HGB，
∴∠BGM＝∠HGM＝∠BGH，
∵EM平分∠HED，
∴∠HEM＝∠DEM＝∠HED，
∵MQ∥AB，
∴∠BGM＝∠GMQ，
∵MQ∥CD，
∴∠QME＝∠MED，
∴∠GME＝∠GMQ+∠QME＝∠BGM+∠MED，
∵HP∥AB，
∴∠BGH＝∠GHP＝2∠BGM，
∵HP∥CD，
∴∠PHE＝∠HED＝2∠MED，
∴∠GHE＝∠GHP+∠PHE＝2∠BGM+2∠MED＝2（∠BGM+∠MED），
∴∠GHE＝∠2GME；
（3）过点M作MQ∥AB，过点H作HP∥AB，

由∠KFE：∠MGH＝13：5，设∠KFE＝13x，∠MGH＝5x，
由（2）可知：∠BGH＝2∠MGH＝10x，
∵∠AFE+∠BFE＝180°，
∴∠AFE＝180°﹣10x，
∵FK平分∠AFE，
∴∠AFK＝∠KFE＝ ∠AFE，
即，
解得：x＝5°，
∴∠BGH＝10x＝50°，
∵HP∥AB，HP∥CD，
∴∠BGH＝∠GHP＝50°，∠PHE＝∠HED，
∵∠GHE＝90°，
∴∠PHE＝∠GHE﹣∠GHP＝90°﹣50°＝40°，
∴∠HED＝40°．
【点拨】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质定理以及灵活构造平行线是解题的关键．