高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行达标测试

这是一份高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行达标测试，文件包含人教A版高中数学必修第二册课时分层作业34答案docx、人教A版高中数学必修第二册课时分层作业34线面垂直的性质与空间距离docx等2份试卷配套教学资源，其中试卷共11页， 欢迎下载使用。
2．AB [由线面垂直的性质定理可得AB正确．]
3．C [如图，取BD中点O，连接AO，CO，则BD⊥AO，BD⊥CO，
∴BD⊥平面AOC，BD⊥AC，又BD，AC异面，
∴BD与AC垂直但不相交，
故选C.]
4．B [如图，连接AC，DB交于点O，在正方体ABCD-A1B1C1D1中，
∵DB⊥AC，BB1⊥AC，BB1∩DB＝B，
∴AC⊥平面BDD1B1．
∴点C到平面BDD1B1的距离为CO.
∵AB＝2，∴AC＝22，
∴CO＝12AC＝2.]
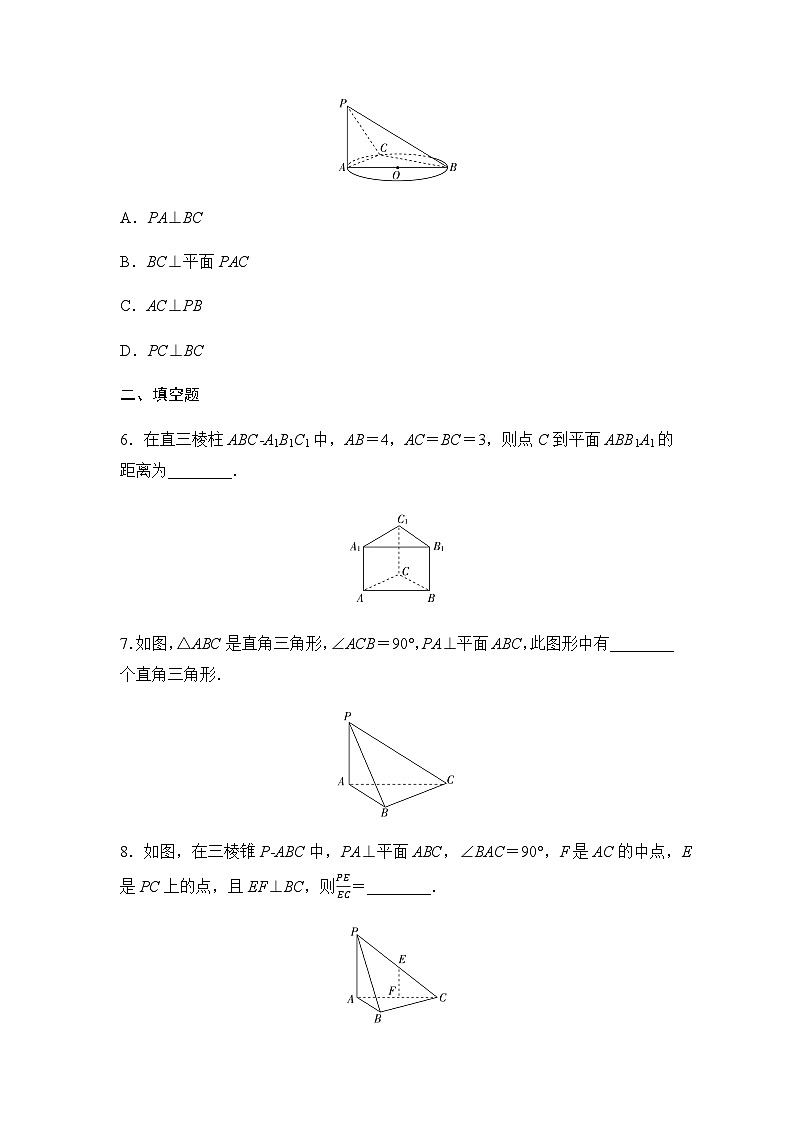
5．ABD [∵PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC，A选项正确；又∵BC⊥AC，PA∩AC＝A，
∴BC⊥平面PAC，又PC⊂平面PAC，∴BC⊥PC，∴B，D选项均正确．故选ABD.]
6．5 [如图，取AB的中点D，连接CD.
因为CA＝CB，所以CD⊥AB.
因为AA1⊥平面ABC，CD⊂平面ABC，所以AA1⊥CD.
因为AB∩AA1＝A，所以CD⊥平面ABB1A1．
所以点C到平面ABB1A1的距离为CD＝BC2-BD2＝5.]
7．4 [∵PA⊥平面ABC，
∴PA⊥AC，PA⊥AB，PA⊥BC，
∵AC⊥BC，且PA∩AC＝A，∴BC⊥平面PAC，
∴BC⊥PC. 综上知：△ABC，△PAC，△PAB，△PBC都是直角三角形，共有4个．]
8．1 [在三棱锥P-ABC中，因为PA⊥平面ABC，∠BAC＝90°，所以AB⊥平面PAC.
因为EF⊂平面PAC，所以EF⊥AB，
因为EF⊥BC，BC∩AB＝B，
所以EF⊥平面ABC，所以PA∥EF，
因为F是AC的中点，E是PC上的点，
所以E是PC的中点，所以PEEC＝1．]
9．解：(1)证明：因为AD＝2PD＝4，PA＝25，所以PA2＝PD2＋AD2，即PD⊥AD，因为CD⊥平面PAD，所以CD⊥PD，且AD∩CD＝D，
所以PD⊥平面ABCD.
(2)因为三棱锥P-ADQ的体积为23，
所以13S△ADQ·PD＝23，所以S△ADQ＝33.
所以12AD·AQ·sin 60°＝33，所以AQ＝3．
所以Q为AB中点，即点A到平面PDQ的距离等于点B到平面PDQ的距离．
在△ADQ中，由余弦定理可得DQ＝AD2+AQ2-2AD·AQcs60°＝13.
所以S△PDQ＝12×PD×DQ＝13.
由VP-ADQ＝VA-PDQ⇒23＝13×13×d，所以d＝63913.
所以点B到平面PDQ的距离为63913.
10．C [由题意知两平面平行，所以原问题等价于求解点C1到平面AB1D1的距离h，由等体积法可得VC1-AB1D1＝VA-B1C1D1，即13×12×22×sin 60°·h＝13×12×2×2×2，解得h＝63，即平面AB1D1到平面BC1D的距离为63.]
11．A [显然DD1是满足条件的一条，如果还有一条l满足条件，则l⊥B1C1，l⊥AB.又AB∥C1D1，则l⊥C1D1．
又B1C1∩C1D1＝C1，所以l⊥平面B1C1D1．
同理DD1⊥平面B1C1D1，则l∥DD1．又l与DD1都过M，这是不可能的，因此只有DD1一条满足条件．]
12．30° [如图，作AC⊥α，BD⊥α，垂足分别为C，D，则AC∥BD，AC，BD确定的平面与平面α交于CD，且CD与AB相交于O，AB＝10 cm，AC＝3 cm，BD＝2 cm，则AO＝6 cm，BO＝4 cm，
∴∠AOC＝∠BOD＝30°，即线段AB与平面α所成的角的大小为30°.]
13．①(或②) [如图所示．
因为PA⊥平面ABCD，QD⊂平面ABCD，
所以PA⊥QD，又PQ⊥QD，PQ∩PA＝P，
所以QD⊥平面PAQ，
因为AQ⊂平面PAQ，
所以QD⊥AQ，
所以Q在以AD为直径的圆上，
若BC边上存在点Q，使PQ⊥QD，
则BC与以AD为直径的圆有公共点，
所以AB≤12AD，即a≤1．
故答案为：①或②.]
14．解：(1)证明：连接BC1，则O为B1C与BC1的交点．
因为侧面BB1C1C为菱形，所以B1C⊥BC1．
又AO⊥平面BB1C1C，所以B1C⊥AO，
故B1C⊥平面ABO.
由于AB⊂平面ABO，故B1C⊥AB.
(2)在平面BB1C1C内作OD⊥BC，垂足为D，连接AD.
在平面AOD内作OH⊥AD，垂足为H.
由于BC⊥AO，BC⊥OD，
故BC⊥平面AOD，所以OH⊥BC.
又OH⊥AD，所以OH⊥平面ABC.
因为∠CBB1＝60°，所以△CBB1为等边三角形．
又BC＝1，可得OD＝34.
由于AC⊥AB1，所以OA＝12B1C＝12.
由OH·AD＝OD·OA，且AD＝OD2+OA2＝74，得OH＝2114.
又O为B1C的中点，所以点B1到平面ABC的距离为217，故三棱柱ABC-A1B1C1的高为217.
15．解：(1)证明：由已知，得PC2＝PA2＋AC2＝25，PB2＝PA2＋AB2＝34，所以PA⊥AC，PA⊥AB.
又AB∩AC＝A，所以PA⊥平面ABC.
(2)假设在线段AB上存在一点E，使得PB⊥平面CEF.
因为CE⊂平面CEF，所以PB⊥CE.
因为PA⊥平面ABC，所以PA⊥CE.
又PA∩PB＝P，所以CE⊥平面PAB.
因为AB⊂平面PAB，所以CE⊥AB.
设BE＝x，因为AB2＝AC2＋BC2，所以∠ACB＝90°，所以BC2＝BE·AB，即32＝5x，所以x＝95，
故在AB上存在点E满足题意，且BE＝95.