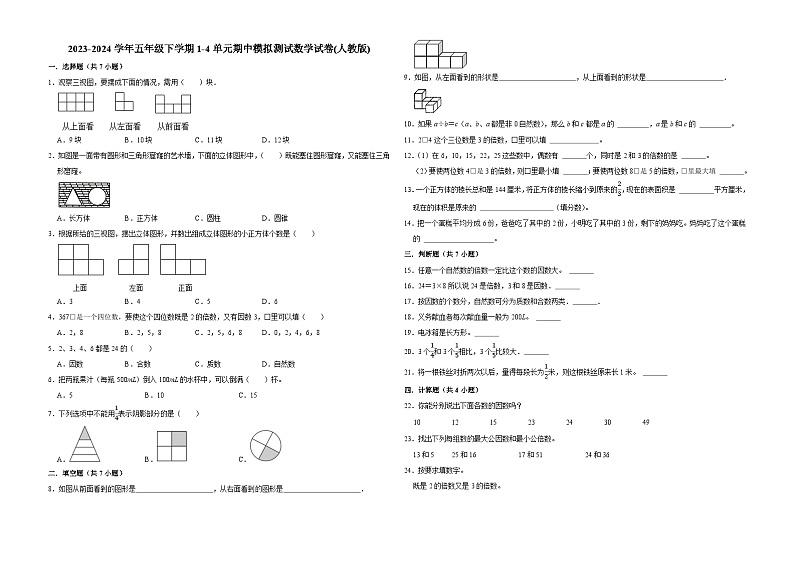
广东省广州市2023-2024学年五年级下学期1-4单元期中模拟测试数学试卷(人教版)

这是一份广东省广州市2023-2024学年五年级下学期1-4单元期中模拟测试数学试卷(人教版)，共8页。试卷主要包含了2、3、4、6都是24的，把两瓶果汁杯等内容，欢迎下载使用。
1．观察三视图，要摆成下面的情况，需用（ ）块．
A．9块B．10块C．11块D．12块
2．如图是一面带有圆形和三角形窟窿的艺术墙，下面的立体图形中，（ ）既能塞住圆形窟窿，又能塞住三角形窟窿。
A．长方体B．正方体C．圆柱D．圆锥
3．根据所给的三视图，摆出立体图形，并数出组成立体图形的小正方体个数是（ ）
A．3B．4C．5D．6
4．367□是一个四位数，要使这个四位数既是2的倍数，又有因数3，□里可以填（ ）
A．2，8B．2，5，8C．2，5，6，8D．0，2，4，6，8
5．2、3、4、6都是24的（ ）
A．因数B．合数C．质数D．自然数
6．把两瓶果汁（每瓶500mL）倒入100mL的水杯中，可以倒满（ ）杯。
A．5B．10C．15
7．下列选项中不能用14表示阴影部分的是（ ）
A．B．C．
二．填空题（共7小题）
8．如图从前面看到的图形是 ，从右面看到的图形是 ．
9．如图，从左面看到的形状是 ，从上面看到的形状是 ．
10．如果a÷b＝c（a、b、a都是非0自然数），那么b和c都是a的 ，a是b和c的 。
11．2□4这个三位数是3的倍数，□里可以填 。
12．（1）在6，10，15，22，25这些数中，偶数有 个，同时是2和3的倍数的是 。
（2）要使两位数4□是3的倍数，则□里最小填 ；要使两位数8□是5的倍数，□里最大填 。
13．一个正方体的棱长总和是144厘米，将正方体的棱长缩小到原来的23，现在的表面积是 平方厘米，现在的体积是原来的 （填分数）。
14．把一个蛋糕平均分成6份，爸爸吃了其中的2份，小明吃了其中的3份，剩下的妈妈吃。妈妈吃了这个蛋糕的 。
三．判断题（共7小题）
15．任意一个自然数的倍数一定比这个数的因数大。
16．24＝3×8所以说24是倍数，3和8是因数．
17．按因数的个数分，自然数可分为质数和合数两类． ．
18．义务献血者每次献血量一般为200L。
19．电冰箱是长方形。
20．3个14和3个15相比，3个15比较大．
21．将一根铁丝对折两次以后，量得每段长为12米，则这根铁丝原来长1米。
四．计算题（共4小题）
22．你能分别说出下面各数的因数吗？
23．找出下列每组数的最大公因数和最小公倍数。
13和5 25和16 17和51 24和36
24．按要求填数字。
既是2的倍数又是3的倍数。
25．求下面各图形的表面积和体积．（单位：分米）
五．操作题（共2小题）
26．画出如图立体图形从正面、上面和左面看到的形状。
27．涂一涂，把如图中的一些〇涂上黑色，使白色的〇是黑色的3倍。
六．应用题（共6小题）
28．有四种规格的饮料包装盒：4瓶/盒、8瓶/盒、9瓶/盒、12瓶/盒。现有60瓶饮料，选哪种规格的饮料包装盒正好能装完？为什么？
29．新源超市新进一批不同包装的牛奶，每箱牛奶价格既是2的倍数又是3的倍数，还是5的倍数。如果最贵的牛奶价格低于100元，最贵多少元？
30．在“迎国庆，庆中秋”文艺晚会中，体操表演队有24名同学要排成每行人数相等的长方形队列，可以怎样排？（每行或每列的人数，不得少于3人）
31．小乐家有一个棱长30cm的正方体收纳箱用来收纳衣物。这个收纳箱的容积是多少立方厘米？（收纳箱的厚度忽略不计）
32．把54块巧克力装在盒子里，每个盒子装得同样多，有几种装法？每种装法各需几个盒子？
33．建一个长50米、宽25米、深2米的长方体游泳池。
（1）这个游泳池占地多少平方米？
（2）要在游泳池四周和底面贴上瓷砖，贴瓷砖的面积是多少平方米？
（3）如果要往这个游泳池里注1.8米深的水，已知每小时注水150立方米，需要注多少小时？
2023-2024学年五年级下学期1-4单元期中模拟测试数学试卷(人教版)
参考答案与试题解析
一．选择题（共7小题）
1．【答案】B
【分析】观察三视图可知，这个几何体共有2层，由俯视图可得第一层小正方体的块数，由正视图和左视图可得第二层有小正方体的块数，相加即可．
【解答】解：由俯视图可得最底层有8块小正方体，由正视图和左视图可得第二层有2块小正方体，
共有8+2＝10（块）．
故选：B．
【点评】此题主要考查了由三视图判断几何体，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，正视图疯狂盖，左视图拆违章”就更容易得到答案．
2．【答案】D
【分析】根据圆锥的特征，圆锥的底面是一个圆，侧面是一个曲面，侧面展开是一个扇形。圆锥从正面看是一个三角形，所以只有圆锥既能塞住三角形窟窿，又能塞住圆形窟窿。
【解答】解：根据圆锥的特征可知，圆锥既能塞住圆形窟窿，又能塞住三角形窟窿。
故选：D。
【点评】此题考查的目的是理解掌握圆锥的特征及应用。
3．【答案】D
【分析】根据从上面看的图形可得最下面一层5个小正方形，根据从正面看的图形和从左面看的图形可得第二层应有1个小正方形．
【解答】解：由图可知，这个立体图形的底层应该有3+2＝5个，第二层应该有1个小正方体，因此构成这个立体图形的小正方体的个数是5+1＝6个．
如图：
故选：D．
【点评】本题考查从不同方向观察物体和几何体，本题解题的关键是利用上面、左面、正面图看出下层和上层共有多少个小正方形，加起来得到结果．
4．【答案】A
【分析】同时是2、3的倍数的数的特征：个位上是0、2、4、6、8的数，各个数位上的数加起来能被3整除。
【解答】解：3+6+7
＝9+7
＝16
16+0＝16
16+2＝18
16+4＝20
16+6＝22
16+8＝24
18、24能被3整除。
答：□内可以填2或8。
故选：A。
【点评】本题考查了2和3的倍数特征，要熟练掌握。
5．【答案】A
【分析】求一个数的因数的方法：用这个数分别除以自然数1、2、3、4、5、6……一直除到商和除数互换位置结束，把能整除的商和除数按从小到大顺序写出来，就是这个数的因数，重复的只写一个，据此写出。
【解答】解：24的因数有：1、2、3、4、6、8、12、24，所以2、3、4、6这4个数都是24的因数。
故选：A。
【点评】此题考查了找一个数因数的方法，列举出这个数的所有因数，是解答此题的关键。
6．【答案】B
【分析】先用加法计算出两瓶果汁的总量，然后计算出两瓶果汁的总量里面有几个100mL，有几个100mL就可以倒满几杯，依此解答。
【解答】解：500+500＝1000（mL）
1000mL里面有10个100mL，因此可以倒满10杯。
故选：B。
【点评】熟练掌握对毫升的认识，是解答此题的关键。
7．【答案】A
【分析】把整个图形看作单位“1”，平均分成了4份，阴影部分占1份，用分数表示是14。
【解答】解：图A没有进行平均分，不符合题意；
图B和图C都表示把整个图形看作单位“1”，平均分成了4份，阴影部分占1份，用分数表示是14。
故选：A。
【点评】此题考查了分数的意义，要求学生能够掌握。
二．填空题（共7小题）
8．【答案】见试题解答内容
【分析】这个立体图形由6个相同的小正方体组成，从前面能看到6个正方形，分两行，下行4个，上行2个，左齐；从右面只看到一列2个长方形．
【解答】解：如图，
故答案为：，．
【点评】本题是考查作简单图形的三视图，能正确辨认从正面、上面、左面（或右面）观察到的简单几何体的平面图形．
9．【答案】见试题解答内容
【分析】观察图形可知，从左面看到的图形是2层：下层2个正方形，上层1个靠左边；从上面看到的图形是两行：后面一行3个正方形，前面一行1个正方形靠右边，据此即可画图．
【解答】解：根据题干分析可得：从左面看到的形状是 ，
从上面看到的形状是 ．
故答案为：；．
【点评】本题是考查作简单立体图形的三视图．观察时要注意观察的角度，视线要垂直于被观察面．
10．【答案】因数，倍数。
【分析】若整数a能够被b整除，a叫做b的倍数，b就叫做a的因数，因数与倍数是相互依存的，据此解答。
【解答】解：如果a+b＝c（a、b、a都是非0自然数），那么b和c都是a的因数，a是b和c的倍数。
故答案为：因数，倍数。
【点评】本题主要考查因数与倍数的意义，注意因数与倍数是相互依存的。
11．【答案】0、3、6、9。
【分析】3的倍数特征，各个数位上的数加起来能被3整除。
【解答】解：2+4＝6
6能被3整除。
6+0＝6
6+3＝9
6+6＝12
6+9＝15
6、9、12、15能被3整除。
所以□里可以填0、3、6、9。
故答案为：0、3、6、9。
【点评】本题考查了3的倍数特征，要熟练掌握。
12．【答案】（1）3；6；（2）2；5。
【分析】（1）根据偶数的定义以及2和3的倍数特征解答，偶数：能被2整除的数是偶数，2的倍数特征：个位数字是0、2、4、6或8，3的倍数特征：各个数位上的数相加的和能被3整除；（2）根据3和5的倍数特征解答，5的倍数特征：个位上是0或5。
【解答】解：（1）偶数有6、10、22，3个，
是2的倍数的有6、10、22，
是3的倍数的有6、15，
同时是2和3的倍数的是6；
（2）是3的倍数，4+2＝6、4+5＝9、4+8＝12，□里可以填2、5、8，最小填2，
是5的倍数，□里可以填0或5，最大填5。
故答案为：（1）3；6；（2）2；5。
【点评】解答这道题的关键是熟练掌握2、3和5的倍数特征以及偶数的定义。
13．【答案】384； 827。
【分析】已知正方体的棱长总和是144厘米，根据正方体的棱长总和＝棱长×12，可知正方体的棱长＝棱长总和÷12，据此求出原来正方体的棱长；
又已知正方体的棱长缩小到原来的23，根据求一个数的几分之几是多少，用原来正方体的棱长乘23，求出现在正方体的棱长；
根据正方体的表面积＝棱长×棱长×6，代入数据计算，即可求出现在正方体的表面积；
根据正方体的体积＝棱长×棱长×棱长，以及积的变化规律可知，正方体的棱长缩小到原来的23，那么正方体的体积缩小到原来的（23×23×23），据此解答。
【解答】解：原来正方体的棱长：144÷12＝12（厘米）
现在正方体的棱长：12×23=8（厘米）
现在正方体的表面积：
8×8×6
＝64×6
＝384（平方厘米）
现在的体积是原来的：23×23×23=827
所以，现在的表面积是384平方厘米，现在的体积是原来的827。
故答案为：384； 827。
【点评】本题考查的是正方体的表面积和体积，关键是掌握正方体表面积和体积公式并灵活应用。
14．【答案】16。
【分析】根据分数的意义，把一块蛋糕平均分成6份，其中的每一份是这块蛋糕的16，爸爸和小明共吃了（2+3）份，则妈妈吃了其中的一份，据此解答即可。
【解答】解：2+3＝5（份）
6﹣5＝1（份）
答：把一个蛋糕平均分成6份，爸爸吃了其中的2份，小明吃了其中的3份，剩下的妈妈吃。妈妈吃了这个蛋糕的16。
故答案为：16。
【点评】本题考查了分数的意义。
三．判断题（共7小题）
15．【答案】×
【分析】根据“一个数最大的因数是它本身，最小的倍数是它本身”进行判断即可。
【解答】解：因为一个数最大的因数是它本身，最小的倍数是它本身，即一个数的最大因数和它的最小倍数相等。
所以原题说法错误。
故答案为：×。
【点评】此题应根据因数和倍数的意义进行解答。
16．【答案】见试题解答内容
【分析】因数和倍数是相对的，是相互依存的，只能说一个数是另一个数的倍数或另一个数是这个数的因数，不能单独存在；由此判断即可．
【解答】解：因为3×8＝24，则：24÷3＝8，24是3的倍数，3是24的因数，因数和倍数是相对的，
是相互依存的，不能单独存在，所以本题说法错误；
故答案为：×．
【点评】此题考查了因数和倍数的意义，应明确倍数和因数是相对的，一个不能独立存在．
17．【答案】×
【分析】1既不是质数，也不是合数．由此判断即可．
【解答】解：按约数的个数分，自然数可分为质数、合数和1三类．说成分为质数和合数两类是错误的．
故答案为：×．
【点评】解决此题要明确质数和合数的概念，要注意1既不是质数，也不是合数，所以按约数的个数分，自然数可分为质数、合数和1三类．
18．【答案】×
【分析】计量义务献血者每次献血量，用毫升作单位。
【解答】解：义务献血者每次献血量一般为200毫升。
所以题干说法是错误的。
故答案为：×。
【点评】此类问题要联系实际，不能和实际相违背。
19．【答案】×
【分析】长方形是平面图形，而电冰箱是立体图形，电冰箱应是长方体。本题考查立体图形的分类及识别。
【解答】解：电冰箱是长方体而不是长方形。
故答案为：×。
【点评】这道题解题的关键是要会正确的区分平面图形和立体图形。
20．【答案】见试题解答内容
【分析】运用分数的乘法的意义，列出算式计算出结果再进行比较即可．
【解答】解：3×14=34
3×15=35
因为34＞35
所以3个14的结果比较大．
即题干的说法是错误的．
故答案为：×．
【点评】本题考查了分数乘法的意义及分数大小的比较．
21．【答案】×
【分析】将一根铁丝对折两次，是把这根铁丝平均分成了4份，每段长12米，这根铁丝有4个为12米，用乘法解答。
【解答】解：4×12=2（米）
答：这根铁丝原来长2米。
所以原题说法是错误的。
故答案为：×。
【点评】本题考查了乘法的意义及计算方法。
四．计算题（共4小题）
22．【答案】1，2，5，10；1，2，3，4，6，12；1，3，5，15；1，23；1，2，3，4，6，8，12，24；1，2，3，5，6，10，15，30；1，7，49。
【分析】根据找一个数的因数的方法，可以一对一对的找，最小的是1，最大的是它本身。
【解答】解：10＝1×10＝2×5
10的因数有：1，2，5，10。
12＝1×12＝2×6＝3×4
12的因数有：1，2，3，4，6，12。
15＝1×15＝3×5
15的因数有：1，3，5，15。
23＝1×23
23的因数有：1，23。
24＝1×24＝2×12＝3×8＝4×6
24的因数有：1，2，3，4，6，8，12，24。
30＝1×30＝2×15＝3×10＝5×6
30的因数有：1，2，3，5，6，10，15，30。
49＝1×49＝7×7
49的因数有：1，7，49。
【点评】此题需要学生掌握求一个数因数的方法。
23．【答案】1；65；1；400；17；51；12；72。
【分析】第一个和第二个，13和5为互质数，25和16是互质数，互为互质数的两个数，它们的最大公因数是1，最小公倍数是它们的乘积，据此解答即可；
第三个51是17 的倍数，两个数成倍数关系，较小数是它们的最大公因数，较大数是它们的最小公倍数，据此解答即可。
第四个，根据求两个数的最大公因数的方法和求两个数的最小公倍数的方法，先把两个数分别分解质因数，两个数公有的质因数的乘积是它们的最大公因数，两个数公有的质因数和非公有的质因数的乘积是它们的最小公倍数，据此解答即可。
【解答】解：13和5为互质数，13×5＝65，所以13和5的最大公因数是1，最小公倍数是65；
25和16是互质数，25×16＝400，所以25和16的最大公因数是1，最小公倍数是400；
51÷17＝3，51和17成倍数关系，所以17和51的最大公因数是17，最小公倍数是51。
24＝2×2×2×3，36＝2×2×3×3，2×2×3＝12，2×2×3×2×3＝72，所以24和36的最大公因数是12，最小公倍数是72。
故答案为：1；65；1；400；17；51；12；72。
【点评】此题考查了对求两个数的最大公因数的方法和求两个数的最小公倍数的方法的灵活运用，还考查了当两个数成倍数关系时和互为互质数时，求两个数的最大公因数的方法和求两个数的最小公倍数的方法。
24．【答案】4；1、4、7；2、5、8；2、8。
【分析】根据2、3的倍数的特征，个位上是0、2、4、6、8的数都是2的倍数；一个数各位上的数字之和是3的倍数，这个数一定是3的倍数；既是2的倍数又是3的倍数的数，个位上是0、2、4、6、8且各位上的数字之和是3的倍数。据此解答即可。
【解答】解：既是2的倍数又是3的倍数。
故答案为：4；1、4、7；2、5、8；2、8。
【点评】此题考查的目的是理解掌握2、3的倍数的特征及应用，关键是明确：既是2的倍数又是3的倍数的数，个位上是0、2、4、6、8且各位上的数字之和是3的倍数。
25．【答案】见试题解答内容
【分析】（1）根据长方体的表面积公式：S＝（ab+ah+bh）×2，体积公式：V＝abh，把数据分别代入公式解答．
（2）根据正方体的表面积公式：S＝6a2，体积公式：V＝a3，把数据代入公式解答．
（3）由于正方体和长方体粘合在一起，所以在计算表面积时，长方体只求上下、前后4个面，正方体计算它的表面积，它的体积等于正方体与长方体的体积和．据此解答．
【解答】解：（1）12×6×2+12×3.5×2+6×3.5×2
＝144+84+42
＝270（平方方米）
12×6×3.5＝252（立方分米）
答：这个长方体的表面积是270平方分米，体积是252立方分米．
（2）7×7×6＝294（平方分米）
7×7×7＝343（立方分米）
答：这个正方体的表面积是294平方分米，体积是343立方分米．
（3）2×2×6+3×1×2+3×2×2
＝24+6+12
＝42（平方分米）
2×2×2+3×2×1
＝8+6
＝14（立方分米）
答：它的表面积是42平方分米，体积是14立方分米．
【点评】此题主要考查长方体、正方体的表面积公式、体积公式的灵活运用，关键是熟记公式．
五．操作题（共2小题）
26．【答案】
【分析】根据观察物体的方法，画出如图立体图形从正面、上面和左面看到的形状即可。
【解答】解：如图：
【点评】此题考查从不同方向观察物体，意在培养学生观察物体的空间思维能力。
27．【答案】
【分析】先数出一共有多少个圆圈，平均分成4份，涂上其中的一份为黑色，即可解答。
【解答】解：12÷4＝3（个）
【点评】本题考查倍的意义。
六．应用题（共6小题）
28．【答案】见试题解答内容
【分析】60能被每盒的瓶数整除，则用这种规格的包装盒正好能装完，否则就不能正好装完。
【解答】解：60÷4＝15
60÷8＝7……4
60÷9＝
60÷12＝5
所以选用4瓶/盒、12瓶/盒的包装盒都能正好装完，因为4和12是60的因数。
【点评】每盒的瓶数只要是60的因数，用这样的包装盒都能正好装完。
29．【答案】答：如果最贵的牛奶价格低于100元，最贵90元。
【分析】每箱牛奶价格既是2的倍数又是3的倍数，还是5的倍数，所以这个牛奶的价格同时要满足2、3、5的倍数特征，同时是2、3、5的倍数特征那么这个数个位是0且每一个数位上数字之和是3的倍数。最贵的牛奶价格是2、3、5的倍数且低于100元。
【解答】解：最贵的牛奶价格是2、3、5的倍数，所以个位是0，十位的数字加0是3的倍数，这个数比100小，所以十位的数尽可能的大，十位为9时，9+0＝9是3的倍数，所以低于100元的最贵的牛奶是90元。
答：如果最贵的牛奶价格低于100元，最贵90元。
【点评】本题需要学生熟练掌握2、3、5的倍数特征并能灵活的运用。
30．【答案】3行8列或4行6列。
【分析】每行或每列最少3人，则24＝3×8＝4×6，据此解答。
【解答】解：因为24＝3×8＝4×6，所以可排成3行8列或4行6列。
答：可排成3行8列或4行6列。
【点评】本题主要考查了找因数的基础知识。
31．【答案】27000立方厘米。
【分析】根据正方体的体积（容积）公式：V＝a3，把数据代入公式解答。
【解答】解：30×30×30
＝900×30
＝27000（立方厘米）
答：这个收纳箱的容积是27000立方厘米。
【点评】此题主要考查正方体的体积（容积）公式的灵活运用，关键是熟记公式。
32．【答案】有8种装法，每个盒子装1块，需要54个盒子；每个盒子装54块，需要1个盒子；每个盒子装2块，需要27个盒子；每个盒子装27块，需要2个盒子；每个盒子装3块，需要18个盒子；每个盒子装18块，需要3个盒子；每个盒子装6块，需要9个盒子；每个盒子装9块，需要6个盒子。
【分析】找出54所有的因数即可解答。
【解答】解：54＝1×54，54＝2×27，54＝3×18，54＝6×9
答：有8种装法，每个盒子装1块，需要54个盒子；每个盒子装54块，需要1个盒子；每个盒子装2块，需要27个盒子；每个盒子装27块，需要2个盒子；每个盒子装3块，需要18个盒子；每个盒子装18块，需要3个盒子；每个盒子装6块，需要9个盒子；每个盒子装9块，需要6个盒子。
【点评】本题考查了求一个因数的方法。
33．【答案】（1）1250平方米；
（2）1550平方米；
（3）15小时。
【分析】（1）根据长方形的面积公式：S＝ab，把数据代入公式解答。
（2）根据无盖长方体的表面积公式：S＝ab+2ah+2bh，把数据代入公式解答。
（3）根据长方体的体积公式：V＝abh，把数据代入公式求出这个游泳池内水的体积，然后根据“包含”除法的意义，用游泳池内水的体积除以每小时注入水的体积即可。
【解答】解：（1）50×25＝1250（平方米）
答：这个游泳池占地1250平方米。
（2）50×25+2×25×2+2×50×2
＝1250+100+200
＝1550（平方米）
答：贴瓷砖的面积是1550平方米
（3）50×25×1.8÷150
＝1250×1.8÷150
＝2250÷150
＝15（小时）
答：需要15个小时。
【点评】此题主要考查长方形的面积公式、长方体的表面积公式、体积公式的灵活运用，关键是熟记公式。10
12
15
23
24
30
49
5□
5□0
□52
154□
5□4
5□0 1、4、7
□52 2、5、8
154□2、8