山东省聊城市阳谷县实验中学2023-2024学年七年级下学期3月月考数学试题（原卷版+解析版）

这是一份山东省聊城市阳谷县实验中学2023-2024学年七年级下学期3月月考数学试题（原卷版+解析版），文件包含山东省聊城市阳谷县实验中学2023-2024学年七年级下学期3月月考数学试题原卷版docx、山东省聊城市阳谷县实验中学2023-2024学年七年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

一、选择题（共12小题，共48分）
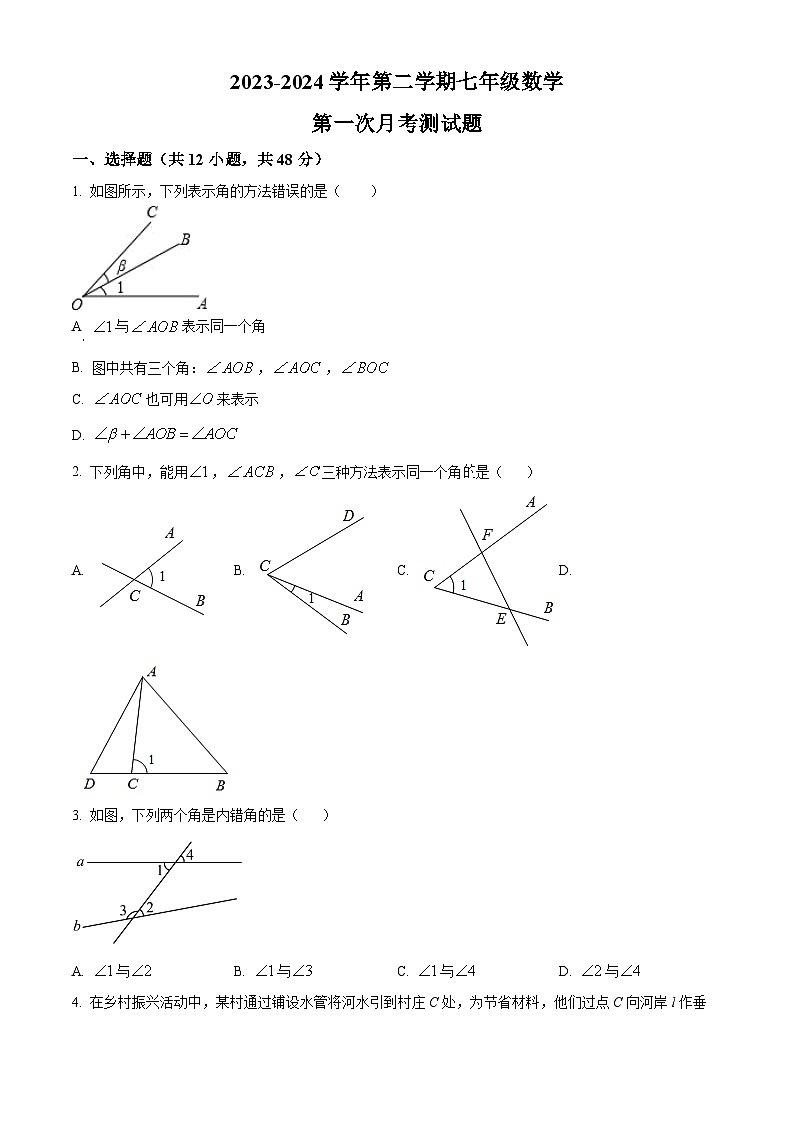
1. 如图所示，下列表示角的方法错误的是（ ）
A. 与表示同一个角
B. 图中共有三个角：，，
C. 也可用来表示
D.
【答案】C
【解析】
【分析】根据角表示方法、角的和差进行判断即可．
【详解】解：A．与表示同一个角，故选项正确，不符合题意；
B．图中共有三个角：，，，故选项正确，不符合题意；
C．不可用来表示，故选项错误，符合题意；
D．，故选项正确，不符合题意．
故选：C．
【点睛】此题考查了角，熟练掌握角的表示方法、角的和差是解题的关键．
2. 下列角中，能用，，三种方法表示同一个角的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据角表示方法，顶点只存在一个角时，可以用一个字母表示角，据此分析即可
【详解】根据角的表示方法，顶点只存在一个角时，可以用一个字母表示角，
A、B、D选项中，点为顶点的角存在多个，故不符合题意
故选C
【点睛】本题考查了角的表示方法，掌握角的表示方法是解题的关键．角的表示方法有三种：（1）用三个字母及符号“∠”来表示．中间的字母表示顶点，其它两个字母分别表示角的两边上的点．（2）用一个数字表示一个角．（3）用一个字母表示一个角．具体用哪种方法，要根据角的情况进行具体分析，总之表示要明确，不能使人产生误解．
3. 如图，下列两个角是内错角的是（ ）
A. 与B. 与C. 与D. 与
【答案】A
【解析】
【分析】此题考查了同位角、内错角、同旁内角、对顶角等知识，根据两角之间的关系进行判断即可.
【详解】解：根据图形可知，与是内错角，与是同旁内角，与是对顶角，与是同位角，
故选：A
4. 在乡村振兴活动中，某村通过铺设水管将河水引到村庄C处，为节省材料，他们过点C向河岸l作垂线，垂足为点D，于是确定沿CD铺设水管，这样做的数学道理是（ ）
A. 两点之间，线段最短B. 过一点有且只有一条直线与已知直线垂直
C. 垂线段最短D. 两条直线相交有且只有一个交点
【答案】C
【解析】
【分析】根据垂线段最短进行判断．
【详解】解：因为于点，根据垂线段最短，所以为点到河岸的最短路径．
故选：C．
【点睛】本题考查了垂线段及其性质：从直线外一点引一条直线的垂线，这点和垂足之间的线段叫做垂线段，垂线段最短．
5. 据中国载人航天工程办公室消息，北京时间2021年12月9日15点40分，“天宫课堂”第一课正式开讲．在时刻15：40时，时钟上的时针与分针之间所成的夹角是（ ）
A. 150°B. 120°C. 130°D. 140°
【答案】C
【解析】
【分析】根据时钟上一大格是，时针1分钟转进行计算即可．
【详解】解：由题意得：
，
在时刻时，时钟上的时针与分针之间所成的夹角是：，
故选：C．
【点睛】本题考查了方向角，解题的关键是熟练掌握时钟上一大格是，时针1分钟转．
6. 若，，，则（ ）
A. B. C. D. 以上都不对
【答案】C
【解析】
【分析】根据把化成度数再进行解答即可．
【详解】解：，
，
，
A、B均错误，不合题意，
C正确，符合题意．
故选：C．
【点睛】此题考查了角的换算，比较大小，比较简单，解答此题的关键是熟知．
7. 如图，下列结论中，不能说明射线平分的是（ ）

A. B.
C. D.
【答案】D
【解析】
【分析】根据角平分线的性质，可得答案．
【详解】A、∵∠AOC＝∠BOC，∴OC平分∠AOB，故A正确；
B、∵∠AOB＝2∠AOC，∠AOB＝∠AOC＋∠BOC，∴∠AOC＝∠BOC，故B正确；
C、∵∠AOB＝2∠BOC，∠AOB＝∠AOC＋∠BOC，∴∠AOC＝∠BOC，故C正确；
D、∵∠AOC＋∠BOC＝∠AOB，∠AOC不一定等于∠BOC，故D错误；
故选：D．
【点睛】本题考查角平分线判定，掌握角平分线的判定是解题的关键．
8. 如图，点O在直线上，，那么图中互余的角有（ ）

A 3对B. 4对C. 5对D. 6对
【答案】B
【解析】
【分析】本题主要考查了余角的定义，熟知互余的两个角的度数之和为90度是解题的关键．根据互余的两个角的度数之和为90度进行推理即可．
【详解】解：∵点O在直线上，，
∴，
∴，，，，
∴互余角的对数共有4对．
故选：B．
9. 如图，，，，如图所示，则下列各式中正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】根据平行线的性质，可以得到∠1，∠2，∠3之间的关系，从而可以解答本题．
【详解】解：∵l1∥l2∥l3，
∴∠1=∠2+∠4，∠4+∠3=180°，
∴∠1-∠2+∠3=180°，
故选：C．
【点睛】本题考查平行线的性质，解答本题的关键是明确题意，利用数形结合的思想解答．
10. 如果是方程组的解，则的值为（ ）
A. 1B. 2C. 3D. 4
【答案】C
【解析】
【分析】此题考查了二元一次方程组的解和解方程组，根据方程组的解得到关于a、b的方程组，解方程组得到a、b的值，代入代数式即可得到答案.
【详解】解：∵是方程组的解，
∴
①＋②得，
解得，
把代入①得，
解得，
∴，
故选：C
11. 数学课上， 老师要求同学们利用三角板画两条平行线．小明的画法如下：①将含角的三角尺的最长边与直线a重合，另一块三角尺最长边与含角的三角尺的最短边紧贴；②将含角的三角尺沿贴合边平移一段距离，画出最长边所在直线b，则a∥b，小明这样画图的依据是（ ）
A. 同位角相等，两直线平行B. 内错角相等，两直线平行
C. 同旁内角互补，两直线平行D. 两直线平行，同位角相等
【答案】A
【解析】
【分析】先利用平移的性质得到∠1=∠2=60°，然后根据同位角线段两直线平行可判断a∥b．
【详解】利用平移的性质得到
∠1=∠2=60°，
所以a∥b．
故选：A．
【点睛】此题考查作图-平移变换，平行线的判定，解题关键在于确定平移后图形的基本要素有两个：平移方向、平移距离．作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形．
12. 下列说法中正确的个数有（ ）
①在同一平面内，不重合的两条直线的位置关系为平行或垂直；②过一点有且只有一条直线与已知直线平行；③平行于同一直线的两条直线互相平行；④垂直于同一直线的两条直线互相平行；
A. 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
【分析】此题考查了直线的位置关系，根据直线的位置关系的相关知识进行判断即可.
【详解】解：①在同一平面内，不重合的两条直线的位置关系为平行或相交，故选项错误；
②过直线外一点有且只有一条直线与已知直线平行，故选项错误；
③平行于同一直线的两条直线互相平行，故选项正确；
④同一平面内，垂直于同一直线的两条直线互相平行，故选项错误；
正确的有1个，
故选：A
二、填空题（共6小题，共24分）
13. 如图，已知点O是直线AB上一点，，射线OD、OE将三等分，则=_________.
【答案】
【解析】
【分析】根据邻补角求出的度数，再根据三等分求出的度数，最后根据角的和与差即可得出答案.
【详解】
射线OD、OE将三等分
故答案为：.
【点睛】本题考查了邻补角的有关计算，及角的n等分，结合图形找到角直角的关系是解题的关键.
14. 已知关于x、y的方程组的解是，则________、________．
【答案】 ①. 5 ②. 1
【解析】
【分析】本题主要考查了二元一次方程组的解，准确计算是解题的关键．把代入中，得到关于a，b的方程组求解即可．
【详解】解：把代入中得到：
，
解得：．
故答案为：5；1．
15. 如图，等腰直角三角板的顶点A，C分别在直线a，b上，若a∥b，∠1=35°，则∠2的度数为________．
【答案】10°
【解析】
【分析】先求出，根据两直线平行，内错角相等即可求出∠4的度数，易知∠2的度数.
【详解】解：如图，
由题意可知

又


故答案是10°
【点睛】本题考查两直线平行，内错角相等，灵活运用等腰直角三角形中的角是解题的关键.
16. 比较大小：________（填、或）
比较大小：________．（填、或）
【答案】 ①. ②.
【解析】
【分析】此题考查了度分秒之间的转换和比较度数大小，单位统一后进行比较即可得到答案．
【详解】解：，
∵，
∴
故答案为：
，，
∴，
故答案为：
17. 在庆祝“中国共产党建党一百周年”之际，小明用长方形彩色纸条折叠蝴蝶结．把一张长方形纸条按图中那样折叠后，若得到，则________．
【答案】##125度
【解析】
【分析】此题考查了折叠和平行线的性质，熟记“两直线平行，同旁内角互补”及折叠的性质是解题的关键．根据平角的定义得到，根据折叠的性质得到，最后根据平行线的性质求解即可．
【详解】解：∵，，
∴，
∵四边形由四边形折叠而成，
∴，
∵四边形是长方形，
∴，
∴，
∴
故答案为：．
18. 将一块三角板ABC（∠BAC=90°，∠ABC=30°）按如图方式放置，使A，B两点分别落在直线m，n上，对于给出的五个条件：①∠1=25.5°，∠2=55°；②∠1+∠2=90°；③∠2=2∠1；④∠ACB=∠1+∠3；⑤∠ABC=∠2-∠1．能判断直线mn的有__．（填序号）
【答案】①④⑤
【解析】
【分析】根据平行线的判定方法和题目中各个小题中的条件，逐一判断是否可以得到m∥n，从而可以解答本题．
【详解】解：∵∠1=25.5°，∠2=55°，∠ABC=30°，
∴∠ABC+∠1=55.5°=55°=∠2，
∴mn，故①符合题意；
∵∠1+∠2=90°，∠ABC=30°，
∴∠1+∠ABC不一定等于∠2，
∴m和n不一定平行，故②不符合题意；
∵∠2=2∠1，∠ABC=30°，
∴∠1+∠ABC不一定等于∠2，
∴m和n不一定平行，故③不符合题意；
过点C作CEm，
∴∠3=∠4，
∵∠ACB=∠1+∠3，∠ACB=∠4+∠5，
∴∠1=∠5，
∴ECn，
∴mn，故④符合题意；
∵∠ABC=∠2-∠1，
∴∠2=∠ABC+∠1，
∴mn，故⑤符合题意；
故答案为：①④⑤．
【点睛】本题考查平行线的判定，解答本题的关键是明确题意，利用数形结合的思想解答．
三、解答题（共7小题7+8+16+10+10+12+15）
19. 如图，以B为顶点的角有几个？把它们表示出来．以D为顶点且小于平角的角有几个？把它们表示出来．
【答案】图中以B为顶点的角有∠ABD，∠ABC，∠DBC共3个；
以D为顶点且小于平角角有∠ADE，∠ADB，∠BDC，∠EDC共4个．
【解析】
【详解】【试题分析】考查角的定义，有公共端点的两条射线组成的图形，则以点B为顶点的角有3个，分别为∠ABD，∠ABC，∠DBC；以D为顶点且小于平角的角有∠ADE，∠ADB，∠BDC，∠EDC共4个.
【试题解析】
图中以B为顶点的角有∠ABD，∠ABC，∠DBC，共3个；
以D为顶点且小于平角的角有∠ADE，∠ADB，∠BDC，∠EDC，共4个．
20. 如图，点，分别在直线，上．
（1）在图中作出表示，两点间的距离的线段和表示点到直线的距离的线段；
（2）比较(1)中线段，的大小，并说明理由．
【答案】（1）见解析 （2），理由是垂线段最短
【解析】
【分析】（1）根据线段的意义，点到直线的距离，可得答案；
（2）根据垂线段的性质，可得答案．
【小问1详解】
解：连接，过作，如图所示，
【小问2详解】
由垂线段最短，得
，
即，
理由是垂线段最短．
【点睛】本题考查了点到直线的距离，利用垂线段的性质是解题关键
21. 解下列二元一次方程组：
（1）；
（2）；
（3）；
（4）．
【答案】（1）
（2）
（3）
（4）
【解析】
【分析】本题主要考查了解二元一次方程组，解题的关键是熟练掌握解二元一次方程组的方法，准确计算．
（1）用代入消元法解二元一次方程组即可；
（2）用加减消元法解二元一次方程组即可；
（3）用加减消元法解二元一次方程组即可；
（4）用加减消元法解二元一次方程组即可．
【小问1详解】
解：，
把①代入②得：，
解得：，
把代入①得，
∴原方程组的解为．
【小问2详解】
解：，
得：，
把代入①得：，
解得：，
∴原方程组的解为．
【小问3详解】
解：，
原方程组可变为：，
得：，
解得：，
把代入②得：，
解得：，
∴原方程组的解为．
【小问4详解】
解：，
原方程可变为，
得：，
解得：，
把代入②得：，
解得：，
∴原方程组的解为．
22. 已知关于x，y的方程组和的解相同，求的值．
【答案】1
【解析】
【分析】此题考查了二元一次方程组的解，解二元一次方程组，乘方的性质，解题的关键是掌握二元一次方程组的求解，正确求得的值．由题意可得：方程组和方程组的解相同，求得的值，代入求解即可．
【详解】解：由题意可得：方程组和方程组的解相同，
解方程组可得：，
将代入可得：，
解得：，
将代入可得，原式，
即的值．
23. 如图，已知平分：：4，求的度数.
【答案】135°
【解析】
【详解】试题分析：首先根据∠BOE：∠AOB=1：4，且这两个角的度数的和是90°，即可求得∠BOE的度数，根据角平分线的定义即可求得∠BOD的度数，然后根据周角的定义即可求得．
试题解析：

：：4

又OE为的平分线


24. 如图，CD//AB，∠DCB＝70°，∠CBF＝20°，∠EFB＝130°．
（1）直线EF与AB有怎样的位置关系？说明理由；
（2）若∠CEF＝68°，则∠ACB的度数是多少？
【答案】（1）平行，理由见解析；（2）42゜
【解析】
【分析】（1）由题意推出∠DCB=∠ABC=70°，结合∠CBF=20°，推出∠CBF=50°，即可推出EF∥AB；
（2）根据（1）推出的结论，推出EF∥CD，既而推出∠ECD=112°，根据∠DCB=70°，即可推出∠ACB的度数．
【详解】解：（1）EF和AB的关系为平行关系．理由如下：
∵CD∥AB，∠DCB=70°，
∴∠DCB=∠ABC=70°，
∵∠CBF=20°，
∴∠ABF=∠ABC∠CBF=50°，
∵∠EFB=130°，
∴∠ABF+∠EFB=50°+130°=180°，
∴EF∥AB；
（2）∵EF∥AB，CD∥AB，
∴EF∥CD，
∵∠CEF=68°，
∴∠ECD=112°，
∵∠DCB=70°，
∴∠ACB=∠ECD∠DCB，
∴∠ACB=42°．
【点睛】本题主要考查平行线的判定和性质定理，关键在于（1）求出∠ABC的度数，（2）熟练运用已知和已证的结论，推出∠ECD=112°，熟练运用平行线的判定定理和性质定理．
25. 如图，，，平分．
（1）与平行吗？说明理由．
（2）与的位置关系如何？为什么？
（3）若，求出的度数．
【答案】（1）平行，理由见解析
（2）平行，理由见解析
（3）
【解析】
【分析】此题考查了平行线的判定和性质，熟练掌握平行线的判定和性质进行正确推理是关键．
（1）根据同位角相等两直线平行即可得到结论；
（2）证明，根据同位角相等两直线平行即可得到结论；
（3）先利用平行线的性质得到，再由角平分线的定义得到，即可得到答案．
【小问1详解】
平行，理由如下：
∵，
∴
∴
小问2详解】
平行，理由如下：
∵
∴
∵，
∴
∴
【小问3详解】
∵
∴，
∵平分．
∴，
∴
∴