2023-2024学年贵州省新高考协作体高二（下）入学数学试卷（含解析）

展开

这是一份2023-2024学年贵州省新高考协作体高二（下）入学数学试卷（含解析），共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1.已知区间M=(−1,3)，N=(−1,1)，则∁MN=( )
A. (−1,1)B. (1,3)C. [1,3)D. (3,+∞]
2.已知tanθ=−12，则sin2θ=( )
A. −45B. −25C. 25D. 45
3.若函数y=ax+b−1(a>0且a≠1)的图象经过第二、三、四象限，则一定有( )
A. 00B. a>1，且b>0
C. 01，且b<0
4.已知非零复数z满足z2=z−(z−为z的共轭复数)，则z的模为( )
A. 1B. 34C. 12D. 14
5.已知双曲线C的中心在坐标原点，焦点在y轴上，其中一条渐近线的方程为3x+4y=0，则双曲线C的离心率为( )
A. 43B. 53C. 54D. 3 77
6.在△ABC中，已知csA=1213，sinB=35，则csC等于( )
A. −3365B. 6365C. −3365或6365D. 3365或6365
7.我校高二(1)班周一有语文、数学、英语、物理、化学、体育和班会共7节课，已知体育不能排在第一、二节，且数学课的前一节课不能是体育课，班会课只能在第六、七节，则该班周一的排课方法共有( )
A. 840种B. 868种C. 912种D. 936种
8.如图，O1是正四面体的内切球，球O2，O3，O4，O5分别是四个角处与球O1及正四面体的三个侧面都相切的球.则球O1的体积与球O2，O3，O4，O5的体积之和的比为( )
A. 1：2
B. 1：1
C. 3：2
D. 2：1
二、多选题：本题共4小题，共20分。在每小题给出的选项中，有多项符合题目要求。
9.已知向量a=(−1,2)，b=(1,m)，则( )
A. 若a//b，则m的值为−2
B. 与a方向相同的单位向量e=(− 55,2 55)
C. 若m=3，则=45°
D. a与b夹角为钝角的充要条件是m<12
10.已知m，n为两条不同的直线，α，β两个不同的平面，且m⊥α，n//β，则( )
A. 若m//n，则α⊥βB. 若m//β，则m⊥n
C. 若m⊥β，则m⊥nD. 若m//n，则m//β
11.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图象如图所示，下列说法正确的是( )
A. ω=2
B. 函数y=f(x−π6)为偶函数
C. 函数y=f(x)的图象关于直线x=−5π12对称
D. 函数y=f(x)在[−π3,π12]上的最小值为− 3
12.已知定义在R上的函数f(x)满足f(1)=1且f(x+y)+f(x−y)=f(x)f(y)，则( )
A. f(0)=2B. f(2)=0C. f(x)为偶函数D. f(x)为周期函数
三、填空题：本题共4小题，每小题5分，共20分。
13.已知直线l过点(0,1)和(− 2,3)，则直线l的一般式方程为______．
14.已知关于x的不等式mx2+3mx−12<0的解集为R，则实数m的取值范围是______．
15.在(x2−4x+4)5的展开式中，含x7项的系数为______(用数字作答)．
16.已知抛物线C：y2=2px(p>0)的焦点为F，过点F的直线与C交于A，B两点，且|AB|=9，|AF|<|BF|若点A的坐标为(1,−2 2)，则|AF||BF|的值为______.过点B作C的准线的垂线，垂足为B1，则|B1A|= ______．
四、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题10分)
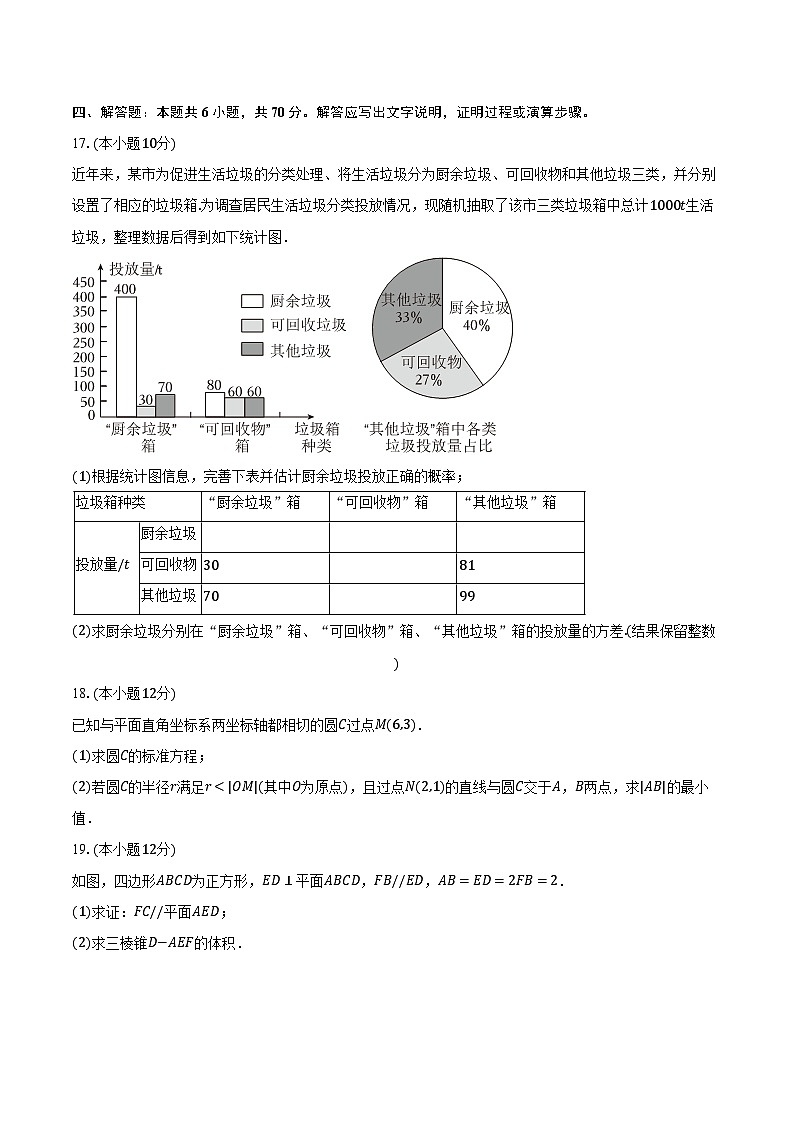
近年来，某市为促进生活垃圾的分类处理、将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000t生活垃圾，整理数据后得到如下统计图．

(1)根据统计图信息，完善下表并估计厨余垃圾投放正确的概率；
(2)求厨余垃圾分别在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差.(结果保留整数)
18.(本小题12分)
已知与平面直角坐标系两坐标轴都相切的圆C过点M(6,3)．
(1)求圆C的标准方程；
(2)若圆C的半径r满足r<|OM|(其中O为原点)，且过点N(2,1)的直线与圆C交于A，B两点，求|AB|的最小值．
19.(本小题12分)
如图，四边形ABCD为正方形，ED⊥平面ABCD，FB//ED，AB=ED=2FB=2．
(1)求证：FC//平面AED；
(2)求三棱锥D−AEF的体积．
20.(本小题12分)
在△ABC中，内角A，B，C的对边分别为a，b，c，若bcsC−ccsB=a．
(1)求角B；
(2)若平面内一点D满足BD=13BC+23BA，且|BD|= 2，求△ABC面积的最大值．
21.(本小题12分)
如图，O是棱长为2的正方体ABCD−A1B1C1D1的中心，E是棱B1C1的中点，P是正方体表面满足OP⊥CE的动点．
(1)举出3个点P的位置(要求：这3个点不共线，无需说明理由)；
(2)记由(1)中所举3个点所确定的平面为α，求平面α与平面BED1所成角的余弦值；
(3)求动点P的轨迹的长度．
22.(本小题12分)
设椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1，F2，M是椭圆上的动点.已知△F1MF2面积的最大值为12，且点F2到点E(72c,0)的距离等于|OF2|，其中c是椭圆的半焦距．
(1)求椭圆的标准方程．
(2)若线段OF1，OF2的中点分别为G，H，过点G作直线l交椭圆于点M，N，则是否存在满足HM⊥HN的直线l？若存在，请求出直线l的方程；若不存在，请说明理由．
答案和解析
1.【答案】C
【解析】解：M=(−1,3)，N=(−1,1)，
则∁MN=[1,3)．
故选：C．
结合补集的定义，即可求解．
本题主要考查补集及其运算，属于基础题．
2.【答案】A
【解析】解：因为tanθ=−12，所以sin2θ=2sinθcsθ=2sinθcsθsin2θ+cs2θ=2tanθtan2θ+1=−45．
故选：A．
根据二倍角公式变形即可求值．
本题考查三角恒等变换，属于基础题．
3.【答案】C
【解析】解：如图所示，图象与y轴的交点在y轴的负半轴上(纵截距小于零)，即a0+b−1<0，且0∴0故选：C．
观察到函数是一个指数型的函数，不妨作出其图象，从图象上看出其是一个减函数，并且是由某个指数函数向下平移而得到的，故可得出结论．
考查指数型函数的图象与性质，本题由函数的图象可以看出其变化趋势，由图象特征推测出参数的范围．
4.【答案】A
【解析】解：设z=a+bi(a,b∈R)，
z2=z−，
则(a+bi)2=a2−b2+2abi=a−bi，即a2−b2=a2ab=−b，解得a=−12，b2=34，
故|z|= a2+b2=1．
故选：A．
根据已知条件，结合复数的四则运算，共轭复数的定义，复数模公式，即可求解．
本题主要考查复数的四则运算，共轭复数的定义，复数模公式，属于基础题．
5.【答案】B
【解析】解：由双曲线C的中心在坐标原点，焦点在y轴上，
设双曲线的方程为y2a2−x2b2=1(a,b>0)，可得渐近线方程为y=±abx，
其中一条渐近线的方程为3x+4y=0，
则ab=34，e=ca= 1+b2a2= 1+169=53．
故选：B．
由焦点在y轴上的双曲线的渐近线方程，可得a，b的方程，由离心率公式可得所求值．
本题考查双曲线的方程和性质，考查方程思想和运算能力，属于基础题．
6.【答案】C
【解析】解：在△ABC中，因为csA=1213，所以sinA= 1−cs2A=513，
因为sinB=35，所以csB=± 1−sin2B=±45．
因为A+B+C=π，
所以csC=cs[π−(A+B)]=−cs(A+B)．
当csB=45时，−cs(A+B)=−(csAcsB−sinAsinB)=−(1213×45−513×35)=−3365，
即csC=−3365；
当csB=−45时，−cs(A+B)=−(csAcsB−sinAsinB)=−[1213×(−45)−513×35]=6365，
即csC=6365．
综上可知，csC的值为−3365或6365．
故选：C．
先求得sinA=513，csB=±45，而csC=cs[π−(A+B)]=−cs(A+B)，从而利用和角余弦公式即可求解．
本题考查两角和与差的三角函数及同角三角函数间的基本关系，属于中档题．
7.【答案】A
【解析】解：①班会课安排在第六节课，则该班周一的排课方法有A66−2A55−4A44+2A44=432种，
②班会课安排在第七节课，则该班周一的排课方法有A66−2A55−5A44+2A44=408种，
故该班周一的排课方法共有432+408=840种．
故选：A．
先将班会课按在第六节课和在第七节课两种情况进行分类，再结合总体剔除法计算即可．
本题考查排列组合的应用，属于基础题．
8.【答案】D
【解析】解：如图，设正四面体ABCD的顶点A在底面的射影为H，
则根据对称性可知正四面体ABCD的外接球与内切球同球心，且球心O1在AH上，
设正四面体ABCD的棱长为a，正四面体ABCD外接球与内切球的半径分别为R，r，
则易知BH=23BE=23× 32a= 33a，∴AH= a2−( 3a3)2= 63a，
在Rt△BO1H中，由勾股定理可得O1B2=BH2+O1H2，
∴R2=a23+( 6a3−R)2，解得R= 64a，∴r=O1H=AH−R= 63a− 64a= 612a，
∴r：R=1：3，∴正四面体ABCD的内切球与AH的另一个交点F为AH的中点，
过F作与底面BCD平行的平面PQG，如图，
则可得正四面体APQG与正四面体ABCD相似，且相似比为1：2，
故正四面体APQG与正四面体ABCD的内切球的体积比为1：8，
又根据对称性可知正四面体的四个顶点所对应的小内切球的体积相等，
故球O1的体积与球O2，O3，O4，O5的体积之和的比为81+1+1+1=2．
故选：D．
根据正四面体的外接球与内切球的结论，即可求解．
本题考查正四面体的内切球问题，化归转化思想，属中档题．
9.【答案】ABC
【解析】解：因为向量a=(−1,2)，b=(1,m)，
若a//b，则−m=2，即m=−2，A正确；
e=a|a|=−1 5，2 5)=(− 55，2 55)，B正确；
若m=3，则a=(−1,2)，b=(1,3)，
故a⋅b=−1×1+2×3=5，|a|= 5，|b|= 10，
故cs=5 5×10= 22，
由0≤≤π，
故=π4，C正确；
若a，b的夹角为钝角，则a⋅b=−1+2m<0且a与b不共线，
所以m<12且m≠−2，D错误．
故选：ABC．
由已知结合向量平行的坐标表示检验选项A，结合向量的单位向量检验选项B，结合向量的夹角公式检验选项C，D．
本题主要考查了向量平行的坐标表示，向量夹角的坐标表示，属于中档题．
10.【答案】AC
【解析】解：对于A，由面面垂直的判定定理即可判断α⊥β，故A正确；
对于B，若m⊥α，n//β，m//β可得直线m与直线n可能平行、相交、异面，故B错误；
对于C，若m⊥β，又n//β则m⊥n，故C正确；
对于D，若m//n，n//β，则m//β或m⊂β，故D错误．
故选：AC．
A由面面垂直的判定定理即可判断，BCD由线面之间的关系即可判断．
本题考查空间线面的位置关系的判断，属于中档题．
11.【答案】ACD
【解析】解：由函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图象，
可得A=2．T=4×(π3−π12)=π，则ω=2πT=2，A正确；
2×π12+φ=2kπ+π2，k∈Z，又|φ|<π2，所以φ=π3，所以f(x)=2sin(2x+π3)y=f(x−π6)=2sin2x为奇函数，B错误；
2sin[2×(−5π12)+π3]=−2.所以函数y=f(x)的图象关于直线x=−5π12对称，C正确；
x∈[−π3,π12]时，2x+π3∈[−π3,π6]，所以f(x)min=f(−π3)=− 3，D正确．
故选：ACD．
先利用图象求出解析式，再利用正弦型函数的性质的应用判断A、B、C、D的结论．
本题考查的知识要点：正弦型函数的性质，主要考查学生的理解能力和计算能力，属于中档题．
12.【答案】ACD
【解析】解：因为定义在R上的函数f(x)满足f(1)=1且f(x+y)+f(x−y)=f(x)f(y)，
令x=1，y=0，可得f(1)+f(1)=f(1)f(0)，所以f(0)=2，故A正确；
令x=1，y=1，可得f(2)+f(0)=f(1)f(1)，又f(1)=1，f(0)=2，所以(2)=−1，故B错误；
令x=0，y=x，可得f(x)+f(−x)=f(0)f(x)=2f(x)，所以f(x)=f(−x)，
所以函数f(x)为偶函数，故C正确；
令y=1，可得f(x+1)+f(x−1)=f(x)f(1)=f(x)，
所以f(x+1)=f(x)−f(x−1)，f(x+2)=f(x+1)−f(x)，
f(x+3)=f(x+2)−f(x+1)=−f(x)，
所以f(x+6)=f(x)，即函数f(x)为周期函数，且周期为6，故D正确．
故选：ACD．
令x=1，y=0，可判断A；令x=1，y=1，可判断B；令x=0，y=x，可判断C；令y=1，可判断D．
本题主要考查抽象函数及其应用，考查运算求解能力，属于中档题．
13.【答案】 2x+y−1=0
【解析】解：k=3−1− 2−0=− 2，又直线过点(0,1)，
则直线方程为y−1=− 2x，一般式方程为 2x+y−1=0．
故答案为： 2x+y−1=0．
根据点斜式可得直线方程．
本题考查直线方程的计算，属于基础题．
14.【答案】{m|−163【解析】解：当m=0时，不等式为−12<0，解集为R；
当m≠0时，不等式mx2+3mx−12<0的解集为R，
应满足m<0Δ=9m2−4m×(−12)<0，解得−489综上，实数m的取值范围是{m|−163故答案为：{m|−163讨论m=0和m≠0时，求出不等式mx2+3mx−12<0的解集为R应满足的条件，即可求出m的取值范围．
本题考查了不等式恒成立的应用问题，是基础题．
15.【答案】−960
【解析】解：(x2−4x+4)5=(x−2)10的展开式通项公式为：Tr+1=C10rx10−r(−2)r，
令10−r=7，解得r=3，
故含x7项的系数为C103(−2)3=−960．
故答案为：−960．
根据已知条件，结合二项式定理，即可求解．
本题主要考查二项式定理，属于基础题．
16.【答案】12 9
【解析】解：由A(1,−2 2)在抛物线C上，得8=2p，
所以抛物线C的方程为y2=8x，焦点F的坐标为(2,0)，
如图，由抛物线的定义，知|AF|=|AA1|=1+2=3，
所以|BF|=|AB|−|AF|=9−3=6，所以|AF||BF|=12；
如图，延长BA1交准线于点P，
因为|PA||PB|=|AA1||BB1|，所以A是BP的中点，
在Rt△PBB1中，中线|B1A|=12|BP|=|BA|=9．
故答案为：12；9．
由题意得到抛物线C的方程为y2=8x，焦点F的坐标为(2,0)，利用抛物线的定义得到|AF|=|AA1|=1+2=3，|BF|=|AB|−|AF|=9−3=6，即可求解|AF||BF|，延长BA1交准线于点P，利用直角三角形的中线性质即可求解|B1A|．
本题考查了抛物线的性质，属于中档题．
17.【答案】解：(1)由题意可知，“厨余垃圾”箱中一共有垃圾500t，“可回收物”箱中一共有垃圾200t，
所以“其他垃圾”箱中一共有垃圾300t，
再由扇形图可知，“其他垃圾”箱中厨余垃圾有300×40%=120t，可回收垃圾300×27%=81t，其他垃圾300×33%=99t，
补全表格如下：
厨余垃圾投放正确的概率为400400+80+120=23；
(2)厨余垃圾分别在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量为400，80，120，
平均数为400+80+1203=200，
所以方差为13×[(400−200)2+(80−200)2+(120−200)2]≈20267．
【解析】(1)根据统计图中数据信息求解即可；
(2)利用方差的定义求解．
本题主要考查了统计图的应用，考查了方差的定义，属于基础题．
18.【答案】解：(1)圆C过点M(6,3).且圆C与两坐标轴均相切．
设圆C：(x−a)2+(y−b)2=r2，
∵圆C过点M(6,3)，∴(6−a)2+(3−b)2=r2，
又∵圆C两坐标轴均相切，∴得a>0，b>0且a=b=r，
则(6−r)2+(3−r)2=r2，解得r=3或r=15，
即a=b=r=3或者a=b=r=15，
即圆C的标准方程为(x−3)2+(y−3)2=9或(x−15)2+(y−15)2=225；
(2)若圆C的半径r满足r<|OM|= 62+32=3 5(其中O为原点)，
即圆C的标准方程为(x−3)2+(y−3)2=9，
直线l过圆C内一定点N(2,1)，
当CN⊥AB时，|AB|有最小值，
CN= (3−2)2+(3−1)2= 5，
∴|AB|的最小值|AB|min=2 r2−CN2=2 9−5=4．
【解析】(1)设圆C：(x−a)2+(y−b)2=r2，由圆C过点M(6,3)代入方程，再根据圆C与两坐标轴均相切得出a>0，b>0，且a=b=r，解出r，即可得出圆C的方程；
(2)直线l过圆C内一定点P(3,1)，当CP⊥AB时，|AB|有最小值，由此能求出|AB|的最小值．
本题主要考查直线与圆的位置关系，考查转化能力，属于中档题．
19.【答案】解：(1)证明：∵四边形ABCD为正方形，
∴BC//AD，又BC⊄平面平面AED，AD⊂平面AED，
∴BC//平面AED，
又FB//ED，同理可得FB//平面AED，
又BF∩BC=B，且BF，BC⊂平面BFC，
∴平面BFC//平面AED，又FC⊂平面BFC，
∴FC//平面AED；
(2)由题意易知BA⊥平面AED，
∴B到平面的距离为AB，
又由(1)知FB//平面AED，
又四边形ABCD为正方形，AB=ED=2FB=2，
∴F到平面ADE的距离等于B到平面ADE的距离，
∴三棱锥D−AEF的体积为13×S△ADE×AB=13×12×2×2×2=43．
【解析】(1)根据面面平行的判定定理与性质，即可证明；
(2)转化三棱锥的顶点，再根据三棱锥的体积公式，即可求解．
本题考查线面平行的证明，三棱锥的体积的求解，属基础题．
20.【答案】解：(1)因为bcsC−ccsB=a，由正弦定理可得sinBcsC−sinCcsB=sinA，
即sin(B−C)=sinA=sin(C+B)，
在△ABC中，可得B−C=B+C或B−C=π−(B+C)，
可得B=π2；
(2)建立平面直角坐标系，以B为坐标原点，
BA，BC所在是直线分别为x，y轴，设A(a,0)，B(0,b)，
因为D满足BD=13BC+23BA=13(0,b)+23(a,0)=(23a,13b)，
又因为|BD|= 2，所以2=49a2+19b2≥2 49a2⋅19b2，当且仅当49a2=19b2，
即a=32，b=3时取等号，
即ab≤92，
所以S△ABC=12ab≤12⋅92=94，
即△ABC面积的最大值为94．
【解析】(1)由题意及正弦定理可得sin(B−C)=sinA=sin(C+B)，在三角形中，由角之间的关系，可得B角的大小；
(2)由(1)可建立平面直角坐标系，设A，C的坐标，由向量的关系，可得BD的坐标，求出它的模长的不等式，由题意及基本不等式可得ab的乘积的最大值，进而求出△ABC的面积的最大值．
本题考查正弦定理的应用及向量的运算性质的应用，属于中档题．
21.【答案】解：(1)当P为四边形BCC1B1中心时，OP⊥CE；
当P在BB1上，且BP=12时，OP⊥CE；
当P在AA1上，且BP=12时，OP⊥CE．
(2)以D为原点，DA，DC，DD1分别为x轴、y轴、z轴建立空间直角坐标系，

则D(0,0,0)，B(2,2,0)，B1(2,2,2)，C(0,2,0)，C1(0,2,2)，D1(0,0,2)，
因为E是B1C1的中点，所以E(1,2,2)，
所以D1E=(1,2,0)，BE=(−1,0,2)，
设n=(x,y,z)是平面BED1的法向量．
则n⋅D1E=x+2y=0n⋅BE=−x+2z=0，令x=2，得n=(2,−1,1)，
由于(1)中所举的三个点P不共线，且均满足OP⊥CE，
所以平面α为与CE垂直的平面，可取CE=(1,0,2)为其法向量，
所以平面α与平面BED1所成角的余弦值为：
|cs〈n,CE〉|=|n⋅CE|n||CE||=2+2 6⋅ 5=2 3015．
(3)点P的轨迹为如图所示的矩形，

所以点P的轨迹的长度为2×(2+ 5)=4+2 5．
【解析】(1)当P为四边形BCC1B1中心，或当P在BB1上，且BP=12，或当P在AA1上，且BP=12时，OP⊥CE．
(2)以D为原点，DA，DC，DD1分别为x轴、y轴、z轴建立空间直角坐标系，利用向量法能求出平面α与平面BED1所成角的余弦值．
(3)点P的轨迹为矩形，由此能求出点P的轨迹的长度．
本题考查正方体的结构特征、二面角、点的轨迹等基础知识，考查运算求解能力，是中档题．
22.【答案】解：(1)由△F1MF2面积的最大值为12，得12⋅2c⋅b=12，即cb=12，
由|F2N|=|OF2|，得|c−72c|=c，解得c=6，
所以b=2，a2=b2+c2=40，
所以椭圆的标准方程为x240+y24=1；
(2)由题意，得G(−3,0)，H(3,0)，因为直线l过点G，
所以设直线l的方程为x=my−3，设M(x1,y1)，N(x2,y2)，
则HM=(x1−3,y1),HN=(x2−3,y2)，
联立x=my−3x240+y24=1，得(m2+10)y2−6my−31=0，
所以y1+y2=6mm2+10y1y2=−31m2+10，
因为HM⊥HN，
所以HM⋅HN=(x1−3)⋅(x2−3)+y1y2=(m2+1)y1y2−6m(y1+y2)+36=0，
即−31(m2+1)m2+10−36m2m2+10+36=0，解得m=± 1019931，
所以直线l的方程为x= 1019931y−3或x=− 1019931y−3，
即直线l的方程为x− 1019931y+3=0或x+ 1019931y+3=0．
【解析】(1)由椭圆的性质列方程即可求解；
(2)设直线l的方程为x=my−3，设M(x1,y1)，N(x2,y2)，联立直线l与椭圆的方程，由韦达定理可得y1+y2=6mm2+10y1y2=−31m2+10，再由HM⋅HN=(x1−3)⋅(x2−3)+y1y2=(m2+1)y1y2−6m(y1+y2)+36=0，代入即可求解．
本题考查了椭圆的性质及直线与椭圆的位置关系的应用，属于中档题．垃圾箱种类
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
投放量/t
厨余垃圾
可回收物
30
81
其他垃圾
70
99
垃圾箱种类
“厨余垃圾”箱
“可回收物”箱
“其他垃圾”箱
投放量/t
厨余垃圾
400
80
120
可回收物
30
60
81
其他垃圾
70
60
99