




所属成套资源:中考数学二轮复习(知识精讲+真题过关练习)(2份打包,原卷版+解析版)
- 中考数学二轮复习冲刺第08讲 二次函数(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版) 试卷 0 次下载
- 中考数学二轮复习冲刺第09讲几何初步及三角形(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版) 试卷 0 次下载
- 中考数学二轮复习冲刺第11讲 特殊三角形(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版) 试卷 0 次下载
- 中考数学二轮复习冲刺第12讲 勾股定理及其逆定理(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版) 试卷 0 次下载
- 中考数学二轮复习冲刺第13讲 多边形与平行四边形(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版) 试卷 0 次下载
中考数学二轮复习冲刺第10讲 全等三角形(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版)
展开
这是一份中考数学二轮复习冲刺第10讲 全等三角形(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版),文件包含中考数学二轮复习冲刺第10讲全等三角形知识精讲+真题练+模拟练+自招练原卷版doc、中考数学二轮复习冲刺第10讲全等三角形知识精讲+真题练+模拟练+自招练解析版doc等2份试卷配套教学资源,其中试卷共106页, 欢迎下载使用。
1. 掌握全等三角形的概念和性质,能够准确地辨认全等三角形中的对应元素;
2.探索三角形全等的判定方法,能利用三角形全等进行证明,掌握综合法证明的格式;
3. 善于发现和利用隐含的等量元素,如公共角、公共边、对顶角等,灵活选择适当的方法判定两个三角形全等.
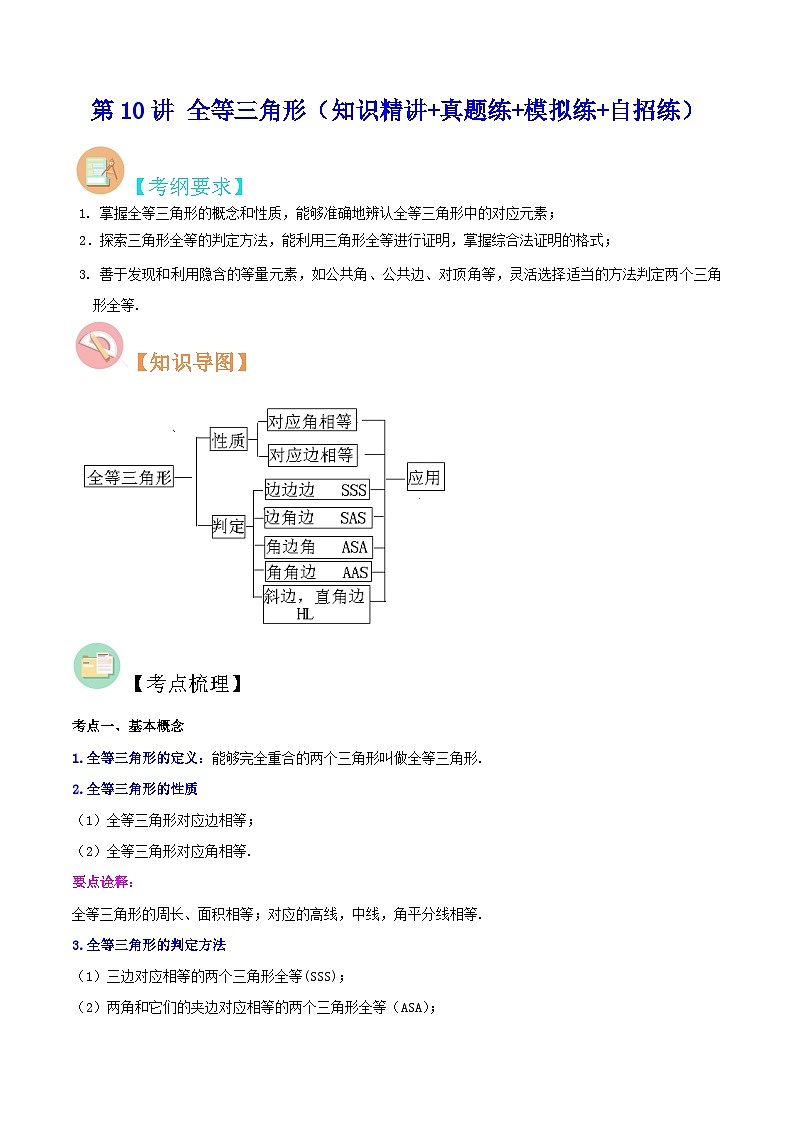
【知识导图】
【考点梳理】
考点一、基本概念
1.全等三角形的定义:能够完全重合的两个三角形叫做全等三角形.
2.全等三角形的性质
(1)全等三角形对应边相等;
(2)全等三角形对应角相等.
要点诠释:
全等三角形的周长、面积相等;对应的高线,中线,角平分线相等.
3.全等三角形的判定方法
(1)三边对应相等的两个三角形全等(SSS);
(2)两角和它们的夹边对应相等的两个三角形全等(ASA);
(3)两角和其中一角的对边对应相等的两个三角形全等(AAS);
(4)两边和它们的夹角对应相等的两个三角形全等(SAS);
(5)斜边和一条直角边对应相等的两个直角三角形全等(HL).
考点二、灵活运用定理
三角形全等是证明线段相等,角相等的最基本、最常用的方法,这不仅因为全等三角形有很多重要的角相等、线段相等的特征,还在于全等三角形能把已知的线段相等、角相等与未知的结论联系起来.
应用三角形全等的判别方法注意以下几点:
1. 条件充足时直接应用判定定理
要点诠释:在证明与线段或角相等的有关问题时,常常需要先证明线段或角所在的两个三角形全等.这种情况证明两个三角形全等的条件比较充分,只要认真观察图形,结合已知条件分析寻找两个三角形全等的条件即可证明两个三角形全等.
2. 条件不足,会增加条件用判定定理
要点诠释:此类问题实际是指条件开放题,即指题中没有确定的已知条件或已知条件不充分,需要补充三角形全等的条件.解这类问题的基本思路是:执果索因,逆向思维,即从求证入手,逐步分析,探索结论成立的条件,从而得出答案.
3. 条件比较隐蔽时,可通过添加辅助线用判定定理
要点诠释:在证明两个三角形全等时,当边或角的关系不明显时,可通过添加辅助线作为桥梁,沟通边或角的关系,使条件由隐变显,从而顺利运用全等三角形的判别方法证明两个三角形全等.
常见的几种辅助线添加:
①遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”;
②遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形利用的思维模式是全等变换中的“旋转”;
③遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理;
④过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”;
⑤截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分之类的题目.
【典型例题】
题型一、全等三角形
例1.如图,BD、CE分别是△ABC的边AC和AB上的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.求证:(1)AP=AQ;(2)AP⊥AQ.
【思路点拨】本题主要考查了全等三角形的判定及性质问题.
【答案与解析】证明:
(1)∵BD、CE分别是△ABC的边AC和AB上的高,
∴∠1+∠CAE=90°,∠2+∠CAE=90°.
∴∠1=∠2,
∵在△AQC和△PAB中,
∴△AQC≌△PAB.
∴ AP=AQ.
(2)∵ AP=AQ,∠QAC=∠P,
∵∠PAD+∠P=90°,
∴∠PAD+∠QAC=90°,即∠PAQ=90°.
∴AP⊥AQ.
【总结升华】在确定全等条件时,注意隐含条件的寻找.
【变式】如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.
(1)求证:∠ABC=∠EDC;
(2)求证:△ABC≌△EDC.
【答案与解析】(1)证明:在四边形ABCD中,∵∠BAD=∠BCD=90°,
∴90°+∠B+90°+∠ADC=360°,
∴∠B+∠ADC=180°,
又∵∠CDE+∠ADC=180°,
∴∠ABC=∠CDE,
(2)连接AC,由(1)证得∠ABC=∠CDE,
在△ABC和△EDC中,
,
∴△ABC≌△EDC(SAS).
题型二、灵活运用定理
例2.如图,已知AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:BE+CF>EF.
【思路点拨】将所求的线段转移到同一个或相关联的三角形中进行求解.
【答案与解析】证明:延长ED至M,使DM=DE,连接 CM,MF,
在△BDE和△CDM中,
∴△BDE≌△CDM(SAS).
∴BE=CM.
又∵∠1=∠2,∠3=∠4 ,
∠1+∠2+∠3+∠4=180°,
∴∠3+∠2=90°,即∠EDF=90°,
∴∠FDM=∠EDF =90°.
在△EDF和△MDF中
∴△EDF≌△MDF(SAS),
∴EF=MF (全等三角形对应边相等),
∵在△CMF中,CF+CM>MF(三角形两边之和大于第三边),
∴BE+CF>EF.
【总结升华】当涉及到有以线段中点为端点的线段时,可通过延长加倍此线段,构造全等三角形,使题中分散的条件集中.
【变式】如图所示,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF. 求证:AC=BF.
【答案】证明:延长AD到H,使得DH=AD,连结BH,
∵ D为BC中点,
∴BD=DC,
在△ADC和△HDB中
,
∴ △ADC≌△HDB(SAS),
∴ AC=BH, ∠H=∠HAC,
∵ EA=EF,
∴ ∠HAE=∠AFE,
又∵ ∠BFH=∠AFE,
∴ BH=BF,∴ BF=AC.
例3.如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,试判断AB-AD与CD-CB的大小关系,并证明你的结论.
【思路点拨】解答本题的关键是熟练运用三角形中大边对应大角的关系.
【答案与解析】AB-AD>CD-CB;
证明:在AB上取一点E,使得AE=AD,连结CE.
∵AC平分∠BAD,
∵在△ACE和△ACD中,
∴△ACE≌△ACD.
∴CD=CE.
∵在△BCE中,BE>CE-CB,
即AB-AE>CE-CB,
∴AB-AD>CD-CB.
【总结升华】本题也可以延长AD到E,使得AE=AB,连结CE.涉及几条线段的大小关系时,用“截长补短”法构造全等三角形是常用的方法.
【变式】如图所示,已知△ABC中AB>AC,AD是∠BAC的平分线,M是AD上任意一点,
求证:MB-MC<AB-AC.
【答案】
证明:∵AB>AC,在AB上截取AE=AC,连接ME.
在△MBE中,MB-ME<BE(三角形两边之差小于第三边).
在△AMC和△AME中,
∴△AMC≌△AME(SAS).
∴MC=ME(全等三角形的对应边相等).
又∵BE=AB-AE,
∴BE=AB-AC,
∴MB-MC<AB-AC.
例4.如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.
【思路点拨】在AC上取AF=AE,连接OF,即可证得△AEO≌△AFO,得∠AOE=∠AOF;再证得∠COF=∠COD,则根据全等三角形的判定方法AAS即可证△FOC≌△DOC,可得DC=FC,即可得结论.
【答案与解析】在AC上取AF=AE,连接OF,
∵AD平分∠BAC、
∴∠EAO=∠FAO,
在△AEO与△AFO中,
∵
∴△AEO≌△AFO(SAS),
∴∠AOE=∠AOF;
∵AD、CE分别平分∠BAC、∠ACB,
∴∠ECA+∠DAC=(180°-∠B)=60°
则∠AOC=180°-∠ECA-∠DAC=120°;
∴∠AOC=∠DOE=120°,∠AOE=∠COD=∠AOF=60°,(对顶角相等)
则∠COF=60°,
∴∠COD=∠COF,
又∵∠FCO=∠DCO,CO=CO,
∴△FOC≌△DOC(ASA),
∴DC=FC,
∵AC=AF+FC,
∴AC=AE+CD.
【总结升华】本题考查了全等三角形的判定和性质,涉及到三角形内角和定理,熟练掌握全等三角形的判定方法是解题的关键.
题型三、综合运用
例5.如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC中点,BD平分∠ABC,点F在AB上,且BF=BC.
求证:(1)DF=AE;(2)DF⊥AC.
【思路点拨】(1)由等边三角形的性质可写出结论.
(2)要证明以上结论,需创造一些条件,首先可从△ABC中分出一部分使得与△ACF的面积相等,则过A作AM∥FC交BC于M,连接DM、EM,就可创造出这样的条件,然后再证其它的面积也相等即可.
【答案与解析】
证明:(1)延长DE交AB于点G,连接AD.
∵四边形BCDE是平行四边形,
∴ED∥BC,ED=BC.
∵点E是AC的中点,∠ABC=90°,
∴AG=BG,DG⊥AB.
∴AD=BD,
∴∠BAD=∠ABD.
∵BD平分∠ABC,
∴∠ABD=∠BAD=45°,即∠BDE=∠ADE=45°.
又BF=BC,
∴BF=DE.
∴在△AED与△DFB中,,
∴△AED≌△DFB(SAS),
∴AE=DF,即DF=AE;
(2)设AC与FD交于点O.
∵由(1)知,△AED≌△DFB,
∴∠AED=∠DFB,
∴∠DEO=∠DFG.
∵∠DFG+∠FDG=90°,
∴∠DEO+∠EDO=90°,
∴∠EOD=90°,即DF⊥AC.
【总结升华】本题考查了平行四边形的性质,全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.
【变式】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交CE于点G,连结BE. 下列结论中:① CE=BD; ② △ADC是等腰直角三角形;③ ∠ADB=∠AEB; ④ CD·AE=EF·CG;一定正确的结论有( ) .
A.1个 B.2个 C.3个 D.4个
A
B
C
D
E
F
G
【答案】D.
例6.如图,已知△ABC.
(1)请你在BC边上分别取两点D、E(BC的中点除外),连结AD、AE,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
(2)请你根据使(1)成立的相应条件,证明AB+AC>AD+AE.
【思路点拨】考查了三角形面积的求法,全等三角形的判定以及三角形三边的关系.本题(2)中通过构建全等三角形将已知和所求条件转化到相关的三角形中是解题的关键.
【答案与解析】
(1)令BD=CE≠DE,有△ABD和△ACE,△ABE和△ACD面积相等.
(2)取DE的中点O,连结AO并延长到F点,使得FO=AO,连结EF,CF.
在△AD0和△FEO中,又∠AOD=∠FOE,DO=EO,
可证△ADO≌△FEO.
所以AD=FE.
因为BD=CE,DO=EO,
所以BO=CO.
同理可证△ABD≌△FCO,
所以AB=FC.
延长AE交CF于G点,
在△ACG中,AC+CG>AE+EG,
在△EFG中,EG+FG>EF,
可推得AC+CG+EG+FG>AE+EG+EF,
即AC+CF>AE+EF,
所以AB+AC>AD+AE.
【总结升华】正确构造全等和利用三角形的任意两边之和大于第三边的结论是关键.
【变式】在△ABC中,,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图①的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图②的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图③的位置时,试问:DE、AD、BE有怎样的等量关系?请写出这个等量关系,并加以证明.
【答案】
证明:∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,
∴∠DAC=∠BCE.
又AC=BC,∠ADC=∠BEC=90°,
∴△ADC≌△CEB.
∴CD=BE,AD=CE.
∴DE=CE+CD=AD+BE.
(2)证明:∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,
∴∠DAC=∠BCE.
又AC=BC,∠ADC=∠BEC=90°,
∴△ADC≌△CEB.
∴CD=BE,AD=CE.
∴DE=AD-BE.
(3)证明:∵∠ACD+∠BCE=90°∠DAC+∠ACD=90°,
∴∠DAC=∠BCE.
又AC=BC,∠ADC=∠BEC=90°,
∴△ADC≌△CEB.
∴CD=BE,AD=CE.
∴DE=BE-AD.
【中考过关真题练】
一.选择题(共9小题)
1.(2022•成都)如图,在△ABC和△DEF中,点A,E,B,D在同一直线上,AC∥DF,AC=DF,只添加一个条件,能判定△ABC≌△DEF的是( )
A.BC=DEB.AE=DBC.∠A=∠DEFD.∠ABC=∠D
【分析】先根据平行线的性质得到∠A=∠D,加上AC=DF,则可根据全等三角形的判定方法对各选项进行判断.
【解答】解:∵AC∥DF,
∴∠A=∠D,
∵AC=DF,
∴当添加∠C=∠F时,可根据“ASA”判定△ABC≌△DEF;
当添加∠ABC=∠DEF时,可根据“AAS”判定△ABC≌△DEF;
当添加AB=DE时,即AE=BD,可根据“SAS”判定△ABC≌△DEF.
故选:B.
【点评】本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法是解决问题的根据,选用哪一种方法,取决于题目中的已知条件.
2.(2022•扬州)如图,小明家仿古家具的一块三角形状的玻璃坏了,需要重新配一块.小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,CAB.AB,BC,∠BC.AB,AC,∠BD.∠A,∠B,BC
【分析】直接利用全等三角形的判定方法分析得出答案.
【解答】解:A.利用三角形三边对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
B.利用三角形两边、且夹角对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
C.AB,AC,∠B,无法确定三角形的形状,故此选项符合题意;
D.根据∠A,∠B,BC,三角形形状确定,故此选项不合题意;
故选:C.
【点评】此题主要考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
3.(2022•金华)如图,AC与BD相交于点O,OA=OD,OB=OC,不添加辅助线,判定△ABO≌△DCO的依据是( )
A.SSSB.SASC.AASD.HL
【分析】根据题目中的条件和全等三角形的判定方法,可以得到判定△ABO≌△DCO的依据.
【解答】解:在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
故选:B.
【点评】本题考查全等三角形的判定,解答本题的关键是明确题意,写出△AOB和△DOC全等的证明过程.
4.(2022•云南)如图,OB平分∠AOC,D、E、F分别是射线OA、射线OB、射线OC上的点,D、E、F与O点都不重合,连接ED、EF.若添加下列条件中的某一个,就能使△DOE≌△FOE.你认为要添加的那个条件是( )
A.OD=OEB.OE=OFC.∠ODE=∠OEDD.∠ODE=∠OFE
【分析】由OB平分∠AOC,得∠DOE=∠FOE,由OE=OE,可知∠ODE=∠OFE,即可根据AAS得△DOE≌△FOE,可得答案.
【解答】解:∵OB平分∠AOC,
∴∠DOE=∠FOE,
又OE=OE,
若∠ODE=∠OFE,则根据AAS可得△DOE≌△FOE,故选项D符合题意,
而增加OD=OE不能得到△DOE≌△FOE,故选项A不符合题意,
增加OE=OF不能得到△DOE≌△FOE,故选项B不符合题意,
增加∠ODE=∠OED不能得到△DOE≌△FOE,故选项C不符合题意,
故选:D.
【点评】本题考查全等三角形的判定,解题的关键是掌握全等三角形判定定理并会应用.
5.(2022•梧州)如图,在△ABC中,AB=AC,AD是△ABC的角平分线,过点D分别作DE⊥AB,DF⊥AC,垂足分别是点E,F,则下列结论错误的是( )
A.∠ADC=90°B.DE=DFC.AD=BCD.BD=CD
【分析】由等腰三角形的性质可得AD⊥BC,BD=CD,∠B=∠C,由“AAS”可证△BDE≌△CDF,可得DE=DF.
【解答】解:∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,BD=CD,∠B=∠C,
∴∠ADC=90°,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴DE=DF,
故选:C.
【点评】本题考查了全等三角形的判定和性质,等腰三角形的性质,掌握等腰三角形的性质是解题的关键.
6.(2022•泰安)如图,平行四边形ABCD的对角线AC,BD相交于点O,点E为BC的中点,连接EO并延长交AD于点F,∠ABC=60°,BC=2AB.下列结论:①AB⊥AC;②AD=4OE;③四边形AECF是菱形;④S△BOE=S△ABC,其中正确结论的个数是( )
A.4B.3C.2D.1
【分析】通过判定△ABE为等边三角形求得∠BAE=60°,利用等腰三角形的性质求得∠EAC=30°,从而判断①;利用有一组邻边相等的平行四边形是菱形判断③,然后结合菱形的性质和含30°直角三角形的性质判断②;根据三角形中线的性质判断④.
【解答】解:∵点E为BC的中点,
∴BC=2BE=2CE,
又∵BC=2AB,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴∠BAE=∠BEA=60°,
∴∠EAC=∠ECA=30°,
∴∠BAC=∠BAE+∠EAC=90°,
即AB⊥AC,故①正确;
在平行四边形ABCD中,AD∥BC,AD=BC,AO=CO,
∴∠CAD=∠ACB,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∴四边形AECF是平行四边形,
又∵AB⊥AC,点E为BC的中点,
∴AE=CE,
∴平行四边形AECF是菱形,故③正确;
∴AC⊥EF,
在Rt△COE中,∠ACE=30°,
∴OE=CE=BC=AD,故②正确;
在平行四边形ABCD中,OA=OC,
又∵点E为BC的中点,
∴S△BOE=S△BOC=S△ABC,故④正确;
正确的结论由4个,
故选:A.
【点评】本题考查平行四边形的性质,等边三角形的判定和性质,菱形的判定和性质,含30°的直角三角形的性质,掌握菱形的判定是解题关键.
7.(2022•西宁)如图,∠MON=60°,以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B;分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,画射线OP;连接AB,AP,BP,过点P作PE⊥OM于点E,PF⊥ON于点F.则以下结论错误的是( )
A.△AOB是等边三角形B.PE=PF
C.△PAE≌△PBFD.四边形OAPB是菱形
【分析】利用等边三角形的判定,全等三角形的判定与性质,角平分线的性质,和菱形的判定定理对每个选项进行逐一判断即可得出结论.
【解答】解:∵以点O为圆心,适当长为半径画弧,交OM于点A,交ON于点B,
∴OA=OB,
∵∠MON=60°,
∴△AOB是等边三角形,
∴A的结论正确,不符合题意;
∵分别以点A,B为圆心,大于AB的长为半径画弧,两弧在∠MON的内部相交于点P,
∴PA=PB,
在△OPA和△OPB中,
,
∴△OPA≌△OPB(SSS),
∴∠POA=∠POB.
∵PE⊥OM,PF⊥ON,
∴PE=PF.
∴B的结论正确,不符合题意;
∵PE⊥OM,PF⊥ON,
∴∠PEA=∠PFB=90°.
在Rt△PAE和Rt△PBF中,
,
∴Rt△PAE≌Rt△PBF(HL).
∴C的结论正确,不符合题意;
由作图过程可知:OB与PB不一定相等,
∴四边形OAPB是菱形不成立,
∴D的结论错误,符合题意,
故选:D.
【点评】本题主要考查了等边三角形的判定,全等三角形的判定与性质,角平分线的性质,基本作图和菱形的判定定理,利用基本作图的过程得出线段相等的条件是解题的关键.
8.(2022•湘西州)如图,在Rt△ABC中,∠A=90°,M为BC的中点,H为AB上一点,过点C作CG∥AB,交HM的延长线于点G,若AC=8,AB=6,则四边形ACGH周长的最小值是( )
A.24B.22C.20D.18
【分析】通过证明△BMH≌△CMG可得BH=CG,可得四边形ACGH的周长即为AB+AC+GH,进而可确定当MH⊥AB时,四边形ACGH的周长有最小值,通过证明四边形ACGH为矩形可得HG的长,进而可求解.
【解答】解:∵CG∥AB,
∴∠B=∠MCG,
∵M是BC的中点,
∴BM=CM,
在△BMH和△CMG中,
,
∴△BMH≌△CMG(ASA),
∴HM=GM,BH=CG,
∵AB=6,AC=8,
∴四边形ACGH的周长=AC+CG+AH+GH=AB+AC+GH=14+GH,
∴当GH最小时,即MH⊥AB时四边形ACGH的周长有最小值,
∵∠A=90°,MH⊥AB,
∴GH∥AC,
∴四边形ACGH为矩形,
∴GH=8,
∴四边形ACGH的周长最小值为14+8=22,
故选:B.
【点评】本题主要考查全等三角形的判定与性质,确定GH的值是解题的关键.
9.(2022•淄博)如图,在△ABC中,AB=AC,点D在AC边上,过△ABD的内心I作IE⊥BD于点E.若BD=10,CD=4,则BE的长为( )
A.6B.7C.8D.9
【分析】如图,连接AI,BI,CI,DI,过点I作IT⊥AC于点T.证明△IDT≌△IDE(AAS),推出DE=DT,IT=IE,证明Rt△BEI≌Rt△CTI(HL),推出BE=CT,设BE=CT=x,根据DE=DT,可得10﹣x=x﹣4,求出x即可解决问题.
【解答】解:如图,连接AI,BI,CI,DI,过点I作IT⊥AC于点T.
∵I是△ABD的内心,
∴∠BAI=∠CAI,
∵AB=AC,AI=AI,
∴△BAI≌△CAI(SAS),
∴IB=IC,
∵∠ITD=∠IED=90°,∠IDT=∠IDE,DI=DI,
∴△IDT≌△IDE(AAS),
∴DE=DT,IT=IE,
∵∠BEI=∠CTI=90°,
∴Rt△BEI≌Rt△CTI(HL),
∴BE=CT,
设BE=CT=x,
∵DE=DT,
∴10﹣x=x﹣4,
∴x=7,
∴BE=7.
故选:B.
【点评】本题考查三角形的内心,全等三角形的判定和性质,等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
二.填空题(共11小题)
10.(2022•宁夏)如图,AC,BD相交于点O,OB=OD,要使△AOB≌△COD,添加一个条件是 OA=OC(答案不唯一) .(只写一个)
【分析】根据全等三角形的判定方法,即可解答.
【解答】解:∵OB=OD,∠AOB=∠COD,OA=OC,
∴△AOB≌△COD(SAS),
∴要使△AOB≌△COD,添加一个条件是OA=OC,
故答案为:OA=OC(答案不唯一).
【点评】本题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.
11.(2022•湖北)如图,已知AB∥DE,AB=DE,请你添加一个条件 ∠A=∠D ,使△ABC≌△DEF.
【分析】添加条件:∠A=∠D,根据ASA即可证明△ABC≌△DEF.
【解答】解:添加条件:∠A=∠D.
∵AB∥DE,
∴∠B=∠DEC,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA),
故答案为:∠A=∠D.(答案不唯一)
【点评】本题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.
12.(2022•牡丹江)如图,CA=CD,∠ACD=∠BCE,请添加一个条件 CB=CE(答案不唯一) ,使△ABC≌△DEC.
【分析】根据等式的性质可得∠DCE=∠ACB,然后再利用全等三角形的判定方法SAS,ASA或AAS即可解答.
【解答】解:∵∠ACD=∠BCE,
∴∠ACD+∠ACE=∠BCE+∠ACE,
∴∠DCE=∠ACB,
∵CA=CD,CB=CE,
∴△ABC≌△DEC(SAS),
故答案为:CB=CE(答案不唯一).
【点评】本题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.
13.(2022•黑龙江)如图,在四边形ABCD中,对角线AC,BD相交于点O,OA=OC,请你添加一个条件 OB=OD(答案不唯一) ,使△AOB≌△COD.
【分析】此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.
【解答】解:添加的条件是OB=OD,
理由是:在△AOB和△COD中,
,
∴△AOB≌△COD(SAS),
故答案为:OB=OD(答案不唯一).
【点评】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理是SAS,ASA,AAS,SSS,两直角三角形全等还有HL等.
14.(2022•株洲)如图所示,点O在一块直角三角板ABC上(其中∠ABC=30°),OM⊥AB于点M,ON⊥BC于点N,若OM=ON,则∠ABO= 15 度.
【分析】方法一:根据OM⊥AB,ON⊥BC,可知∠OMB=∠ONB=90°,从而可证Rt△OMB≌Rt△ONB(HL),根据全等三角形的性质可得∠OBM=∠OBN,即可求出∠ABO的度数.
方法二:根据角平分线的判定定理求解即可.
【解答】解:方法一:∵OM⊥AB,ON⊥BC,
∴∠OMB=∠ONB=90°,
在Rt△OMB和Rt△ONB中,
,
∴Rt△OMB≌Rt△ONB(HL),
∴∠OBM=∠OBN,
∵∠ABC=30°,
∴∠ABO=15°.
方法二:∵OM⊥AB,ON⊥BC,
又∵OM=ON,
∴OB平分∠ABC,
∴∠OBM=∠OBN,
∵∠ABC=30°,
∴∠ABO=15°.
故答案为:15.
【点评】本题考查了全等三角形的判定和性质,熟练掌握判定直角三角形全等特有的方法(HL)是解题的关键.
15.(2022•南充)如图,正方形ABCD边长为1,点E在边AB上(不与A,B重合),将△ADE沿直线DE折叠,点A落在点A1处,连接A1B,将A1B绕点B顺时针旋转90°得到A2B,连接A1A,A1C,A2C.给出下列四个结论:①△ABA1≌△CBA2;②∠ADE+∠A1CB=45°;③点P是直线DE上动点,则CP+A1P的最小值为;④当∠ADE=30°时,△A1BE的面积为.其中正确的结论是 ①②③ .(填写序号)
【分析】①正确.根据SAS证明三角形全等即可;
②正确.过点D作DT⊥CA1于点T,证明∠ADE+∠CDT=45°,∠CDT=∠BCA1即可;
③正确.连接PA,AC.因为A,A1关于DE对称,推出PA=PA1,推出PA1+PC=PA+PC≥AC=,可得结论;
④错误.过点A1作A1H⊥AB于点H,求出EB,A1H,可得结论.
【解答】解:∵四边形ABCD是正方形,
∴BA=BC,∠ABC=90°,
∵∠A1BA2=∠ABC=90°,
∴∠ABA1=∠CBA2,
∵BA1=BA2,
∴△ABA1≌△CBA2(SAS),故①正确,
过点D作DT⊥CA1于点T,
∵CD=DA1,
∴∠CDT=∠A1DT,
∵∠ADE=∠A1DE,∠ADC=90°,
∴∠ADE+∠CDT=45°,
∵∠CDT+∠DCT=90°,∠DCT+∠BCA1=90°,
∴∠CDT=∠BCA1,
∴∠ADE+∠BCA1=45°,故②正确.
连接PA,AC.
∵A,A1关于DE对称,
∴PA=PA1,
∴PA1+PC=PA+PC≥AC=,
∴PA1+PC的最小值为,故③正确,
过点A1作A1H⊥AB于点H,
∵∠ADE=30°,
∴AE=A1E=AD•tan30°=,
∴EB=AB﹣AE=1﹣,
∵∠A1EB=60°,
∴A1H=A1E•sin60°=×=,
∴=×(1﹣)×=,故④错误.
故答案为:①②③.
【点评】本题考查正方形的性质,解直角三角形,翻折变换,全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
16.(2022•大庆)如图,正方形ABCD中,点E,F分别是边AB,BC上的两个动点,且正方形ABCD的周长是△BEF周长的2倍.连接DE,DF分别与对角线AC交于点M,N,给出如下几个结论:①若AE=2,CF=3,则EF=4;②∠EFN+∠EMN=180°;③若AM=2,CN=3,则MN=4;④若=2,BE=3,则EF=4.其中正确结论的序号为 ② .
【分析】根据已知条件可得EF=AE+FC,即可判断①,进而推出∠EDF=45°,判断②正确,作DG⊥EF于点G,连接GM,GN,证明△GMN是直角三角形,结合勾股定理验证③,证明∠BEF=∠MNG=30°,即可判断④.
【解答】解:∵正方形ABCD的周长是△BEF周长的2倍,
∴BE+BF+EF=AB+BC,
∴EF=AE+FC,
若AE=2,CF=3,则EF=2+3=5,故①错误;
如图,在BA的延长线上取点H,使得AH=CF,
在正方形ABCD中,AD=CD,∠HAD=∠FCD=90°,
在△AHD和△CFD中,
,
∴△AHD≌△CFD(SAS),
∴∠CDF=∠ADH,HD=DF,∠H=∠DFC,
又∵EF=AE+CF,
∴EF=AE+AH=EH,
在△DEH和△DEF中,
,
∴△DEH≌△DEF(SSS),
∴∠HDE=∠FDE,∠H=∠EFD,∠HED=∠FED,
∵∠CDF+∠ADF=∠ADH+∠ADF=∠HDF=90°
∴∠EDF=∠HDE=45°,
∵∠H=∠DFC=∠DFE,∠EMN=∠HED+∠EAM=45°+∠DEF,
∴∠EFN+∠EMN=∠DFC+45°+∠DEF=∠DFC+∠EDF+∠DEF=180°,
则∠EFN+∠EMN=180°,故②正确;
如图,作DG⊥EF于点G,连接GM,GN,
在△AED和△GED中,
,
∴△AED≌△GED(AAS),
同理,△GDF≌△CDF(AAS),
∴AG=DG=CF,∠ADE=∠GDE,∠GDF=∠CDF,
∴点A,G关于DE对称轴,C,G关于DF对称,
∴GM=AM,GN=CN,∠EGM=∠EAM=45°,∠NGF=∠NCF=45°,
∴∠MGN=90°,即△GMN是直角三角形,
若AM=2,CN=3,
∴GM=2,GN=3,
在Rt△GMN中,MN==,故③错误;
∵MG=AM,且=2,BE=3,
在Rt△GMN中,sin∠MNG===,
∴∠MNG=30°,
∵∠EFN+∠EMN=180°,∠EMN+∠AME=180°,
且∠CFN=∠EFN,
∴∠AME=∠CFN,
∴2∠AME=2∠CFN,
即∠AMG=∠CFG,
∴∠GMN=∠BFE,
∴∠BEF=∠MNG=30°,
∴cs∠BEF=cs∠MNG==,
∴EF=2,故④错误,
综上,正确结论的序号为②,
故答案为:②.
【点评】本题考查了正方形的性质,轴对称的性质,解直角三角形,全等三角形的性质与判定,题目有一定综合性,通过添加辅助线构造全等三角形是解题关键.
17.(2022•日照)如图,在平面直角坐标系xOy中,点A的坐标为(0,4),P是x轴上一动点,把线段PA绕点P顺时针旋转60°得到线段PF,连接OF,则线段OF长的最小值是 2 .
【分析】方法一:点F运动所形成的图象是一条直线,当OF⊥F1F2时,垂线段OF最短,当点F1在x轴上时,由勾股定理得:P1O=F1O=,进而得P1A=P1F1=AF1=,求得点F1的坐标为(,0),当点F2在y轴上时,求得点F2的坐标为(0,﹣4),最后根据待定系数法,求得直线F1F2的解析式为y=x﹣4,再由线段中垂线性质得出F1F2=AF1=,在Rt△OF1F2中,设点O到F1F2的距离为h,则根据面积法得×OF1×OF2=×F1F2×h,即 ××4=××h,解得h=2,根据垂线段最短,即可得到线段OF的最小值为2.
方法二:如图,在第二象限作等边三角形AOB,连接BP、AF,过点B作BP′⊥x轴于点P′,可证得△BAP≌△OAF(SAS),得出BP=OF,当BP⊥x轴时,BP最小值为2,故OF的最小值为2.
【解答】解:方法一:∵将线段PA绕点P顺时针旋转60°得到线段PF,
∴∠APF=60°,PF=PA,
∴△APF是等边三角形,
∴AP=AF,
如图,当点F1在x轴上时,△P1AF1为等边三角形,
则P1A=P1F1=AF1,∠AP1F1=60°,
∵AO⊥P1F1,
∴P1O=F1O,∠AOP1=90°,
∴∠P1AO=30°,且AO=4,
由勾股定理得:P1O=F1O=,
∴P1A=P1F1=AF1=,
∴点F1的坐标为(,0),
如图,当点F2在y轴上时,
∵△P2AF2为等边三角形,AO⊥P2O,
∴AO=F2O=4,
∴点F2的坐标为(0,﹣4),
∵tan∠OF1F2===,
∴∠OF1F2=60°,
∴点F运动所形成的图象是一条直线,
∴当OF⊥F1F2时,线段OF最短,
设直线F1F2的解析式为y=kx+b,
则 ,
解得,
∴直线F1F2的解析式为y=x﹣4,
∵AO=F2O=4,AO⊥P1F1,
∴F1F2=AF1=,
在Rt△OF1F2中,
设点O到F1F2的距离为h,则
×OF1×OF2=×F1F2×h,
∴××4=××h,
解得h=2,
即线段OF的最小值为2;
方法二:如图,在第二象限作等边三角形AOB,连接BP、AF,
过点B作BP′⊥x轴于点P′,
∵将线段PA绕点P顺时针旋转60°得到线段PF,
∴∠APF=60°,PF=PA,
∴△APF是等边三角形,
∴AP=AF,∠PAF=60°,
∵△AOB是等边三角形,
∴AB=AO=OB=4,∠BAO=60°,
∴∠BAP=60°+∠OAP=∠OAF,
在△BAP和△OAF中,
,
∴△BAP≌△OAF(SAS),
∴BP=OF,
∵P是x轴上一动点,
∴当BP⊥x轴时,BP最小,即点P与点P′重合时BP=BP′最小,
∵∠BOP′=30°,∠BP′O=90°,
∴BP′=OB=×4=2,
∴OF的最小值为2,
故答案为2.
【点评】本题属于三角形的综合题,主要考查了旋转的性质,勾股定理的应用,等边三角形的性质以及待定系数法的运用等,解决问题的关键是作辅助线构造等边三角形以及面积法求最短距离,解题时注意勾股定理、等边三角形三线合一以及方程思想的灵活运用.
18.(2022•包头)如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,D为AB边上一点,且BD=BC,连接CD,以点D为圆心,DC的长为半径作弧,交BC于点E(异于点C),连接DE,则BE的长为 3﹣3 .
【分析】利用等腰直角三角形的性质,等腰三角形的性质,同圆的半径相等,三角形的内角和定理和全等三角形的判定与性质解答即可.
【解答】解:∵∠ACB=90°,AC=BC=3,
∴AB=AC=3,∠A=∠B=45°,
∵BD=BC=3,AC=BC,
∴BD=AC,AD=3﹣3.
∵DC=DE,
∴∠DCE=∠DEC.
∵BD=BC,
∴∠DCE=∠CDB,
∴∠CED=∠CDB,
∵∠CDB=∠CDE+∠EDB,∠CED=∠B+∠EDB,
∴∠CDE=∠B=45°.
∴∠ADC+∠EDB=180°﹣∠CDE=135°.
∵∠ADC+∠ACD=180°﹣∠A=135°,
∴∠ACD=∠EDB.
在△ADC和△BED中,
,
∴△ADC≌△BED(SAS).
∴BE=AD=3﹣3.
故答案为:3﹣3.
【点评】本题主要考查了等腰直角三角形的性质,等腰三角形的性质,同圆的半径相等,三角形的内角和定理和全等三角形的判定与性质,准确找出图中的全等三角形是解题的关键.
19.(2022•朝阳)等边三角形ABC中,D是边BC上的一点,BD=2CD,以AD为边作等边三角形ADE,连接CE.若CE=2,则等边三角形ABC的边长为 3或. .
【分析】分两种情况,先证明△CAE≌△BAD(SAS),再根据全等三角形的性质即可得出答案.
【解答】解:如图,E点在AD的右边,
∵△ADE与△ABC都是等边三角形,
∴AC=AB,AE=AD,∠DAE=∠BAC=60°,
∴∠DAE﹣∠CAD=∠BAC﹣∠CAD,
即∠CAE=∠BAD.
在△CAE和△BAD中,
,
∴△CAE≌△BAD(SAS),
∴CE=BD=2,
∵BD=2CD,
∴CD=1,
∴BC=BD+CD=2+1=3,
∴等边三角形ABC的边长为3,
如图,E点在AD的左边,
同上,△BAE≌△CAD(SAS),
∴BE=CD,∠ABE=∠ACD=60°,
∴∠EBD=120°,
过点E作EF⊥BC交CB的延长线于点F,则∠EBF=60°,
∴EF=BE=CD,BF=BE=CD,
∴CF=BF+BD+CD=CD,
在Rt△EFC中,CE=2,
∴EF2+CF2=CE2=4,
∴+=4,
∴CD=或CD=﹣(舍去),
∴BC=,
∴等边三角形ABC的边长为,
故答案为:3或.
【点评】本题考查了全等三角形的判定与性质,熟练掌握等边三角形的性质,证明△CAE≌△BAD是解题的关键.
20.(2022•深圳)已知△ABC是直角三角形,∠ABC=90°,AB=3,BC=5,AE=2,连接CE,以CE为底作直角三角形CDE,且CD=DE.F是AE边上的一点,连接BD和BF,且∠FBD=45°,则AF长为 .
【分析】将线段BD绕点D顺时针旋转90°,得到线段HD,连接BH,利用SAS证明△EDH≌△CDB,得EH=CB=5,∠HED=∠BCD=90°,从而得出HE∥DC∥AB,则△ABF∽△EHF,即可解决问题.
【解答】解:将线段BD绕点D顺时针旋转90°,得到线段HD,连接BH,延长HE交BC于G,
∴△BDH是等腰直角三角形,
∴∠HBD=45°,
∵∠FBD=45°,
∴点B、F、H共线,
又∵△EDC是等腰直角三角形,
∴HD=BD,∠EDH=∠CDB,ED=CD,
∴△EDH≌△CDB(SAS),
∴EH=CB=5,∠DHE=∠CBD,
∴∠BGH=∠BDH=90°,
∴HE∥AB,
∴△ABF∽△EHF,
∴,
∵AE=2,
∴,
∴AF=,
故答案为:.
【点评】本题主要考查了等腰直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质等知识,作辅助线构造全等三角形是解题的关键.
三.解答题(共8小题)
21.(2022•铜仁市)如图,点C在BD上,AB⊥BD,ED⊥BD,AC⊥CE,AB=CD.求证:△ABC≌△CDE.
【分析】根据一线三垂直模型利用AAS证明△ABC≌△CDE即可.
【解答】证明:∵AB⊥BD,ED⊥BD,AC⊥CE,
∴∠B=∠D=∠ACE=90°,
∴∠DCE+∠DEC=90°,∠BCA+∠DCE=90°,
∴∠BCA=∠DEC,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS).
【点评】本题考查了全等三角形的判定,熟练掌握一线三垂直模型是解题的关键.
22.(2022•益阳)如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
【分析】由垂直的定义可知,∠DEC=∠B=90°,由平行线的性质可得,∠A=∠DCE,进而由ASA可得结论.
【解答】证明:∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°,
∵CD∥AB,
∴∠A=∠DCE,
在△CED和△ABC中,
,
∴△CED≌△ABC(ASA).
【点评】本题主要考查全等三角形的判定,垂直的定义和平行线的性质,熟知全等三角形的判定定理是解题基础.
23.(2022•广州)如图,点D,E在△ABC的边BC上,∠B=∠C,BD=CE,求证:△ABD≌△ACE.
【分析】根据等角对等边可得AB=AC,然后利用SAS证明△ABD≌△ACE,即可解答.
【解答】证明:∵∠B=∠C,
∴AB=AC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS).
【点评】本题考查了全等三角形的判定,熟练掌握全等三角形的判定,以及等腰三角形的判定与性质是解题的关键.
24.(2022•安顺)如图,在Rt△ABC中,∠BAC=90°,AB=AC=1,D是BC边上的一点,以AD为直角边作等腰Rt△ADE,其中∠DAE=90°,连接CE.
(1)求证:△ABD≌△ACE;
(2)若∠BAD=22.5°时,求BD的长.
【分析】(1)由“SAS”可证△ABD≌△ACE;
(2)由等腰三角形三角形的性质可得BC的长,由角度关系可求∠ADC=67.5°=∠CAD,可得AC=CD=1,即可求解.
【解答】(1)证明:∵∠BAC=90°=∠DAE,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠BAC=90°,AB=AC=1,
∴BC=,∠B=∠ACB=45°,
∵∠BAD=22.5°,
∴∠ADC=67.5°=∠CAD,
∴AC=CD=1,
∴BD=﹣1.
【点评】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,证明三角形全等是解题的关键.
25.(2022•兰州)如图1是小军制作的燕子风筝,燕子风筝的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求∠D的大小.
【分析】由∠BAD=∠EAC可得∠BAC=∠EAD,根据SAS可证△BAC≌△EAD,再根据全等三角形的性质即可求解.
【解答】解:∵∠BAD=∠EAC,
∴∠BAD+∠CAD=∠EAC+∠CAD,即∠BAC=∠EAD,
在△BAC与△EAD中,
,
∴△BAC≌△EAD(SAS),
∴∠D=∠C=50°.
【点评】本题考查了全等三角形的判定和性质,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.
26.(2022•黄石)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,且点D在线段BC上,连CE.
(1)求证:△ABD≌△ACE;
(2)若∠EAC=60°,求∠CED的度数.
【分析】(1)可利用SAS证明结论;
(2)由全等三角形的性质可得∠ACE=∠ABD,利用等腰直角三角形的性质可求得∠ACE=∠ABD=∠AED=45°,再根据三角形的内角和定理可求解∠AEC的度数,进而可求可求解
【解答】(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵△ABD≌△ACE,
∴∠ACE=∠ABD,
∵△ABC和△ADE都是等腰直角三角形,
∴∠ACE=∠ABD=∠AED=45°,
∵∠EAC=60°,
∴∠AEC=180°﹣∠ACE﹣∠EAC=180°﹣45°﹣60°=75°,
∴∠CED=∠AEC﹣∠AED=75°﹣45°=30°.
【点评】本题主要考查全等三角形的判定与性质,等腰直角三角形的性质,三角形的内角和定理,掌握全等三角形的判定条件是解题的关键.
27.(2022•资阳)如图,在△ABC中(AB<BC),过点C作CD∥AB,在CD上截取CD=CB,CB上截取CE=AB,连接DE、DB.
(1)求证:△ABC≌△ECD;
(2)若∠A=90°,AB=3,BD=2,求△BCD的面积.
【分析】(1)由CD∥AB得∠ABC=∠ECD,而CD=CB,CE=AB,即可根据全等三角形的判定定理“SAS”证明△ABC≌△ECD;
(2))由∠A=90°,根据全等三角形的对应角相等证明∠BED=∠CED=∠A=90°,设BE=x,由BD2﹣BE2=CD2﹣EC2=DE2,列方程(2)2﹣x2=(3+x)2﹣32,解方程求得符合题意的x的值为2,则BC=5,再根据勾股定理求出DE的长,即可求出△BCD的面积.
【解答】(1)证明:∵CD∥AB,CD=CB,CE=AB,
∴∠ABC=∠ECD,
在△ABC和△ECD中,
,
∴△ABC≌△ECD(SAS).
(2)解:∵∠A=90°,
∴∠CED=∠A=90°,
∴∠BED=180°﹣∠CED=90°,
设BE=x,
∵EC=AB=3,BD=2,
∴CD=BC=3+x,
∵BD2﹣BE2=CD2﹣EC2=DE2,
∴(2)2﹣x2=(3+x)2﹣32,
整理得x2+3x﹣10=0,
解得x1=2,x2=﹣5(不符合题意,舍去),
∴BE=2,BC=3+2=5,
∴DE===4,
∴S△BCD=BC•DE=×5×4=10,
∴△BCD的面积为10.
【点评】此题重点考查平行线的性质、全等三角形的判定与性质、勾股定理、一元二次方程的解法等知识与方法,证明三角形全等以及根据勾股定理列方程是解题的关键.
28.(2022•荆门)如图,已知矩形ABCD中,AB=8,BC=x(0<x<8),将△ACB沿AC对折到△ACE的位置,AE和CD交于点F.
(1)求证:△CEF≌△ADF;
(2)求tan∠DAF的值(用含x的式子表示).
【分析】(1)根据矩形的性质得到∠B=∠D=90°,BC=AD,根据折叠的性质得到BC=CE,∠E=∠B=90°,等量代换得到∠E=∠D=90°,AD=CE,根据AAS证明三角形全等即可;
(2)设DF=a,则CF=8﹣a,根据矩形的性质和折叠的性质证明AF=CF=8﹣a,在Rt△ADF中,根据勾股定理表示出DF的长,根据正切的定义即可得出答案.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠B=∠D=90°,BC=AD,
根据折叠的性质得:BC=CE,∠E=∠B=90°,
∴∠E=∠D=90°,AD=CE,
在△CEF与△ADF中,
,
∴△CEF≌△ADF(AAS);
(2)解:设DF=a,则CF=8﹣a,
∵四边形ABCD是矩形,
∴AB∥CD,AD=BC=x,
∴∠DCA=∠BAC,
根据折叠的性质得:∠EAC=∠BAC,
∴∠DCA=∠EAC,
∴AF=CF=8﹣a,
在Rt△ADF中,
∵AD2+DF2=AF2,
∴x2+a2=(8﹣a)2,
∴a=,
∴tan∠DAF==.
【点评】本题考查了锐角三角函数的定义,全等三角形的判定与性质,矩形的性质,翻折变换(折叠问题),根据矩形的性质和折叠的性质证出AF=CF是解题的关键.
【中考挑战满分模拟练】
一.选择题(共4小题)
1.(2023•金安区校级模拟)如图,已知△ABC中,∠ACB=45°,F是高BD和CE的交点,AD=3,CD=5,则线段BF的长度为( )
A.1B.2C.D.
【分析】根据等腰直角三角形的性质得CD=BD,再利用ASA证明△CDF≌△BDA,得DF=AD,从而得出答案.
【解答】解:∵F是高BD和CE的交点,
∴∠CDF=∠ADB=∠CEB=90°,
∵∠CFD=∠BFE,
∴∠DCF=∠DBA,
∵∠ACB=45°,∠CDB=90°,
∴∠DCB=∠DBC,
∴CD=BD,
在△CDF和△BDA中,
,
∴△CDF≌△BDA(ASA),
∴DF=AD=3,
∴BF=BD﹣DF=5﹣3=2,
故选:B.
【点评】本题主要考查了等腰直角三角形的性质,全等三角形的判定与性质等知识,证明△CDF≌△BDA是解题的关键.
2.(2023•海口一模)如图,将边长6cm的正方形纸片沿虚线剪开,剪成两个全等梯形.已知裁剪线与正方形的一边夹角为60°,则梯形纸片中较短的底边长为( )
A.(3﹣)cmB.(3﹣2)cmC.(6﹣)cmD.(6﹣2)cm
【分析】过M点作ME⊥AD于E点,根据四边形ABCD是正方形,有AD=CD=6,∠C=∠D=90°,由裁剪的两个梯形全等,可得AN=MC;再证明四边形MCDE是矩形,即有MC=ED,ME=CD=6,进而有AN=ED,在Rt△MNE中,解直角三角形可得NE=2,则可得AN=3﹣问题得解.
【解答】解:如图,过M点作ME⊥AD于E点,
∵四边形ABCD是正方形,边长为6,
∴AD=CD=6,∠C=∠D=90°,
∵裁剪的两个梯形全等,
∴AN=MC,
∵ME⊥AD,
∴四边形MCDE是矩形,
∴MC=ED,ME=CD=6,
∴AN=ED,
根据题意有∠MNE=60°,
∴在Rt△MNE中,NE===2,
∴AN+ED=AD﹣NE=6﹣2,
∴AN=3﹣,
即梯形中较短的底为(3﹣)(cm).
故选:A.
【点评】本题主要考查了正方形的、矩形的判定与性质、解直角三角形的应用等知识,根据梯形全等得出AN=MC是解答本题的关键.
3.(2023•三亚一模)如图,在等腰直角三角形ABC中,∠BAC=90°,D为BC的中点,E为边AC上一点(不与端点重合),过点E作EG⊥BC于点G,作EH⊥AD于点H,过点B作BF∥AC交EG的延长线于点F.若AG=3,则阴影部分的面积为( )
A.12B.12.5C.13D.13.5
【分析】设DG=a,CG=b,则CD=a+b,根据勾股定理得出关于x和y的代数式的值,然后用含有x和y的代数式表示出阴影部分的面积,进而求出阴影部分的面积即可.
【解答】解:设DG=a,CG=b,则CD=a+b,
∵△ABC为等腰直角三角形,∠BAC=90°,
∴∠ABC=∠ACB=45°,AB=AC,
又∵D为BC的中点,
∴BD=AD=CD=a+b,BC=2BD=2(a+b),
∵EG⊥BC,EH⊥AD,
∴四边形DGEH为矩形,∠GEC=45°,
∴DH=EG=CG=b,
∵BF∥AC,
∴∠FBG=∠ACB=45°,
∵EF⊥BC,
∴∠F=45°,
∴GF=BG=BD+DG=a+b+a=2a+b,
由勾股定理得,AD2+DG2=AG2,
∴(a+b)2+a2=32,
整理得,2a2+2ab+b2=9,
由题意知,S阴=S△ABC+S△BGF﹣S矩形DGEH
=BC•AD+BG•GF﹣DG•DH
=BD•AD+BG2﹣DG•DH
=(a+b)2+(2a+b)2﹣ab
=a2+2ab+b2+2a2+ab+b2﹣ab
=(2a2+2ab+b2)
=×9
=13.5,
故选:D.
【点评】本题主要考查直角三角形的知识,熟练掌握勾股定理,等腰直角三角形的性质等知识是解题的关键.
4.(2023•金安区校级模拟)两个直角三角板如图摆放,其中∠ACB=∠EDC=90°,∠A=45°,∠E=30°,点B在DE上,若∠ACE=2∠BCD,则∠ABE的大小为( )
A.75°B.45°C.60°D.65°
【分析】设∠BCD=x,则∠ACE=2x,根据三角形的内角和可得∠ECD=60°,进一步可得∠BCE=60°﹣x,再根据∠ACB=90°列方程2x+60°﹣x=90°,可求出x=30°,再根据三角形外角的性质可得∠CBE,进一步即可求出∠ABE的度数.
【解答】解:设∠BCD=x,则∠ACE=2x,
∵∠EDC=90°,∠E=30°,
∴∠ECD=60°,
∴∠BCE=60°﹣x,
∵∠ACB=90°,
∴2x+60°﹣x=90°,
解得x=30°,
∴∠BCD=30°,
∴∠CBE=∠D+∠BCD=90°+30°=120°,
∵∠ACB=90°,∠A=45°,
∴∠ABC=45°,
∴∠ABE=∠CBE﹣∠ABC=120°﹣45°=75°,
故选:A.
【点评】本题考查了直角三角形的性质,涉及三角形的内角和,外角的性质,熟练掌握以上这些知识是解题的关键.
二.填空题(共2小题)
5.(2023•槐荫区模拟)如图,在4×4的正方形网格中,求α+β= 45 度.
【分析】连接BC,根据勾股定理AB=BC==,AC==,根据勾股定理的逆定理得到∠ABC=90°,求得∠BAC=∠ACB=45°,根据全等三角形的性质和平行线的性质即可得到结论.
【解答】解:连接BC,
∵AB=BC==,AC==,
∴AB2+BC2=AC2,
∴∠ABC=90°,
∴∠BAC=∠ACB=45°,
∵AB=BC=,AE=BD=1,BE=CD=2,
∴△ABE≌△BCD,
∴∠ACD=∠ABE=α,
∵AE∥CD,
∴∠DCA=∠CAE=β,
∴α+β=∠BCA=45°,
故答案为:45.
【点评】本题考查了全等图形,勾股定理和勾股定理的逆定理,等腰直角三角形的判定和性质,熟练掌握勾股定理的逆定理是解题的关键.
6.(2023•琼山区一模)如图,在平面直角坐标系xOy中,点A(﹣3,0),B(3,0),C(3,2),如果△ABC与△ABD全等,那么点D的坐标可以是 (3,﹣2)(答案不唯一) (写出一个即可).
【分析】直接利用全等三角形的性质以及坐标与图形的性质即可得出符合题意的答案.
【解答】解:如图所示:延长CB到D,使BD=BC,连接AD,
∵△ABC与△ABD全等,
∴BD=BC,∠ABC=∠ABD=90°,
∵C的坐标为(3,2),
∴D的坐标为(3,﹣2),
故答案为:(3,﹣2)(答案不唯一).
【点评】此题主要考查了全等三角形的性质以及坐标与图形的性质,正确掌握全等图形的性质是解题关键.
三.解答题(共9小题)
7.(2023•秦都区校级模拟)如图,∠C=∠E,AC=AE,点D在BC边上,∠1=∠2,AC和DE相交于点O.求证:△ABC≌△ADE.
【分析】先利用三角形外角性质证明∠ADE=∠B,然后根据“AAS”判断△ABC≌△ADE.
【解答】证明:∵∠ADC=∠1+∠B,
即∠ADE+∠2=∠1+∠B,
而∠1=∠2,
∴∠ADE=∠B,
在△ABC和△ADE中,
∴△ABC≌△ADE(AAS).
【点评】本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法.选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.
8.(2023•广西模拟)校园内有一块四边形的草坪造型,课外活动小组实地测量,并记录数据,根据造型画如图的四边形ABCD,其中AB=CD=2米,AD=BC=3米,∠B=30°.
(1)求证:△ABC≌△CDA;
(2)求草坪造型的面积.
【分析】(1)利用全等三角形的判定方法,结合三边关系得出答案;
(2)直接利用全等三角形的性质以及直角三角形中30度所对边与斜边的关系的得出对应边长,进而得出答案.
【解答】(1)证明:在△ABC和△CDA中,
∵,
∴△ABC≌△CDA(SSS);
(2)解:过点A作AE⊥BC于点E,
∵AB=2米,∠B=30°,
∴AE=1米,
∴S△ABC=×3×1=(平方米),
则S△CDA=(平方米),
∴草坪造型的面积为:2×=3(平方米).
【点评】此题主要考查了全等三角形的判定与性质以及全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.
9.(2023•雁塔区一模)已知,∠ABC=∠DCB,∠ACB=∠DBC,求证:△ABC≌△DCB.
【分析】根据ASA证明△ABC≌△DCB即可.
【解答】证明:在△ABC与△DCB中,
,
∴△ABC≌△DCB(ASA).
【点评】本题考查了全等三角形的判定,熟练掌握三角形全等的判定方法是解题的关键,要注意BC是两个三角形的公共边.
10.(2023•铜川一模)如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.
【分析】由垂直的定义可知,∠DEC=∠B=90°,由平行线的性质可得,∠A=∠DCE,进而由ASA可得结论.
【解答】证明:∵DE⊥AC,∠B=90°,
∴∠DEC=∠B=90°,
∵CD∥AB,
∴∠A=∠DCE,
在△CED和△ABC中,
,
∴△CED≌△ABC(ASA).
【点评】本题主要考查全等三角形的判定,垂直的定义和平行线的性质,熟知全等三角形的判定定理是解题基础.
11.(2023•定远县校级一模)如图①,在等边三角形ABC中,点D在BC边上,点E在AC的延长线上,DA=DE.
(1)求证:∠BAD=∠EDC;
(2)如图②,M是点E关于直线BC的对称点,连接DM,AM,CM,求证:DM=AM.
【分析】(1)利用三角形内角和定理以及三角形的外角的性质解决问题即可;
(2)证明△ADM是等边三角形即可解决问题.
【解答】证明:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACB=∠B=60°,
∴∠BAD=∠BAC﹣∠DAE=60°﹣∠DAE,∠EDC=∠ACB﹣∠E=60°﹣∠E,
又∵DA=DE,
∴∠DAE=∠E,
∴∠BAD=∠EDC.
(2)∵点M是点E关于直线BC的对称点,
∴DM=DE,∠EDC=∠MDC,
∵DA=DE,
∴DM=DA,由(1)可得,∠BAD=∠EDC,
∴∠MDC=∠BAD,
∵在△ABD中,∠BAD+∠ADB=180°﹣∠B=180°﹣60°=120°,
∴∠MDC+∠ADB=120°,
∴∠ADM=180°﹣(∠MDC+∠ADB)=60°,
∴△ADM是等边三角形,
∴DM=AM.
【点评】本题考查轴对称,等边三角形的判定和性质,等腰三角形的性质,三角形外角的性质,三角形内角和定理,平角的定义等知识.解题的关键是理解和掌握等边三角形的判定和性质.
12.(2023•定远县校级一模)如图1,等腰△ABC和等腰△DEC中,AB=AC=AD,DE=DC.
(1)求证:∠BAE=∠D;
(2)如图2,如果AB⊥AC,求BE:EC的值(提示:先求∠D的度数);
(3)延长线段BA交DC于点F.如果△ACF是等腰三角形,且AB=AC=AD=2,求DC的长.
【分析】(1)利用等腰三角形的性质及其三角形的外角和定理;
(2)过点B作BH∥AC交AE延长线于点H,三角形相似对应边成比例得到;
(3)分两种情况讨论:①如图2,AF=CF,②如图3,AC=CF,由直角三角形的性质及相似三角形的判定与性质可得出答案.
【解答】(1)证明:∵AB=AC,
∴∠B=∠ACB,
∵DE=DC,
∴∠DEC=∠DCE,
∵∠BAE=∠DEC﹣∠B,∠DCA=∠DCE﹣∠DCA,
∴∠BAE=∠DCA,
∵AC=AD,
∴∠D=∠DCA,
∴∠BAE=∠D;
(2)解:由(1)知:∠BAE=∠D=∠ACD,
∵AB⊥AC,
∴∠BAC=90°,∠ABC=∠ACB=45°,
∴∠BAC=∠BAE+∠D+∠ACD=90°,
即∠BAE=∠D=∠ACD=30°.
过点B作BH∥AC交AE延长线于点H,
则∠ABH=45°+45°=90°,
在Rt△ABH中,BH:BA=1:,
即BH:AC=1:=:3,
∵BH∥AC,
∴△BHE∽△CHA,
∴BE:EC=BH:AC=:3;
(3)解:①如图2:AF=CF,
∴∠FAC=∠ACF,
由(1)知:∠BAE=∠DAF=∠D,
∴∠DAC=∠D+∠ACF=90°,
∵AC=AD=2,
∴CD=2;
②如图3,AC=CF,
由已知条件知:∠B=∠ACB,∠D=∠ACF,
由(1)知:∠BAE=∠DAF=∠D,
∴AF=DF,
∴∠D=∠ADF=∠ACD,
∴△DAF∽△DCA,
∴DF:AD=AD:DC,
设DC=x,则DF=x﹣2,
∴(x﹣2):2=2:x,
即x2﹣2x﹣4=0,解得x=+1或x=﹣+1<2(舍去).
综上所述CD的长为2或+1.
【点评】本题考查了全等三角形的判定与性质,等腰三角形的性质,直角三角形的性质,相似三角形的判定与性质,正确进行分类讨论是解题的关键.
13.(2023•莲湖区一模)如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.
【分析】根据AB∥CD,可得∠ABD=∠EDC,利用AAS证明△ABD≌△EDC,即可得结论.
【解答】证明:∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴DB=CD.
【点评】本题考查了全等三角形的判定与性质,解决本题的关键是掌握全等三角形的判定与性质.
14.(2023•碑林区校级一模)如图,在△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.若BC=BD,求证:CD=DE.
【分析】先根据条件得出∠ACD=∠BDE,BD=AC,再根据ASA判定△ADC≌△BED,即可得到CD=DE.
【解答】证明:∵AC=BC,
∴∠A=∠B,
∵AC=BC BC=BD,
∴AC=BD,
∵∠CDB=∠A+∠ACD=∠CDE+∠BDE,∠CDE=∠A,
∴∠ACD=∠BDE,
在△ACD与△BDE中,
,
∴△ACD≌△BDE(ASA),
∴CD=DE.
【点评】本题主要考查了全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握等腰三角形的性质,证明三角形全等是解题的关键.
15.(2023•汉阳区校级一模)如图,△ABC中,AB=AC,∠BAC>90°,BD⊥AC垂足为D,点E在AD上,BE平分∠ABD,点F在BD延长线上,BF=CE,延长FE交BC于点H.
(1)求证:∠CBE=45°;
(2)写出线段BH和EH的位置关系和数量关系,并证明.
【分析】(1)由AB=AC,得∠ABC=∠C,可证明∠ABC=∠C=∠DAB,而∠ABE=∠DBE=∠DBA,则∠CBE=(∠DAB+∠DBA)=45°;
(2)延长BA到点G,使AG=AE,连接EG,因为AB=AC,所以BG=CE=BF,即可证明△EBG≌△EBF,得∠G=∠F,可证明∠G=∠DAB,则∠G=∠F=∠C,于是∠BHE=∠C+∠HEC=∠F+∠DEF=90°,得BH⊥EH,由∠HEB=∠HBE=45°,得BH=EH.
【解答】(1)证明:∵BD⊥AC于D,
∴∠BDC=∠FDC=90°,
∴∠DAB+∠DBA=90°,
∵AB=AC,
∴∠ABC=∠C,
∴∠DAB=∠ABC+∠C=2∠ABC,
∴∠ABC=∠C=∠DAB,
∵BE平分∠ABD,
∴∠ABE=∠DBE=∠DBA,
∴∠CBE=∠ABC+∠ABE=(∠DAB+∠DBA)=45°.
(2)解:BH⊥EH,BH=EH,
证明:延长BA到点G,使AG=AE,连接EG,
∵AB=AC,
∴AB+AG=AC+AE,
∴BG=CE,
∵BF=CE,
∴BG=BF,
在△EBG和△EBF中,
,
∴△EBG≌△EBF(SAS),
∴∠G=∠F,
∵∠G=∠AEG,
∴∠DAB=∠G+∠AEG=2∠G,
∴∠G=∠DAB,
∴∠G=∠C,
∴∠F=∠C,
∵∠HEC=∠DEF,
∴∠BHE=∠C+∠HEC=∠F+∠DEF=90°,
∴BH⊥EH,
∵∠HEB=∠HBE=45°,
∴BH=EH.
【点评】此题重点考查等腰三角形的判定与性质、全等三角形的判定与性质、三角形的一个外角等于与它不相邻的两个内角的和等知识,正确地作出所需要的辅助线是解题的关键.
【名校自招练】
一.选择题(共4小题)
1.(2021•江夏区校级自主招生)如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=( )
A.330°B.315°C.310°D.320°
【分析】利用正方形的性质,分别求出多组三角形全等,如∠1和∠7的余角所在的三角形全等,得到∠1+∠7=90°等,可得所求结论.
【解答】解:由图中可知:①∠4=×90°=45°,②∠1和∠7的余角所在的三角形全等
∴∠1+∠7=90°
同理∠2+∠6=90°,∠3+∠5=90°∠4=45°
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=3×90°+45°=315°
故选:B.
【点评】考查了全等三角形的性质与判定;做题时主要利用全等三角形的对应角相等,得到几对角的和的关系,认真观察图形,找到其中的特点是比较关键的.
2.(2022•南岸区自主招生)如图,点F,E在AC上,AD=CB,∠D=∠B.添加一个条件,不一定能证明△ADE≌△CBF的是( )
A.AD∥BCB.DE∥FBC.DE=BFD.AE=CF
【分析】根据全等三角形的判定定理求解即可.
【解答】解:∵AD∥BC,
∴∠A=∠C,
又AD=CB,∠D=∠B,
∴△ADE≌△CBF(ASA),
故A不符合题意;
∵DE∥FB,
∴∠AED=∠CFB,
又AD=CB,∠D=∠B,
∴△ADE≌△CBF(AAS),
故B不符合题意;
∵DE=BF,
又AD=CB,∠D=∠B,
∴△ADE≌△CBF(SAS),
故C不符合题意;
∵AE=CF,
又AD=CB,∠D=∠B,
不能判定△ADE≌△CBF,
故D符合题意,
故选:D.
【点评】此题考查了全等三角形的判定,熟记全等三角形的判定定理是解题的关键.
3.(2021•武进区校级自主招生)Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
①(BE+CF)=BC;
②S△AEF≤S△ABC;
③S四边形AEDF=AD•EF;
④AD≥EF;
⑤AD与EF可能互相平分,
其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
【分析】先由ASA证明△AED≌△CFD,得出AE=CF,再由勾股定理即可得出BE+CF=AB=BC,从而判断①;
设AB=AC=a,AE=CF=x,先由三角形的面积公式得出S△AEF=﹣(x﹣a)2+a2,S△ABC=×a2=a2,再根据二次函数的性质即可判断②;
由勾股定理得到EF的表达式,利用二次函数性质求得EF最小值为a,而AD=a,所以EF≥AD,从而④错误;
先得出S四边形AEDF=S△ADC=AD,再由EF≥AD得到AD•EF≥AD2,∴AD•EF>S四边形AEDF,所以③错误;
如果四边形AEDF为平行四边形,则AD与EF互相平分,此时DF∥AB,DE∥AC,又D为BC中点,所以当E、F分别为AB、AC的中点时,AD与EF互相平分,从而判断⑤.
【解答】解:∵Rt△ABC中,AB=AC,点D为BC中点,
∴∠C=∠BAD=45°,AD=BD=CD,
∵∠MDN=90°,
∴∠ADE+∠ADF=∠ADF+∠CDF=90°,
∴∠ADE=∠CDF.
在△AED与△CFD中,
∵,
∴△AED≌△CFD(ASA),
∴AE=CF,
在Rt△ABD中,BE+CF=BE+AE=AB==BD=BC.
故①正确;
设AB=AC=a,AE=CF=x,则AF=a﹣x.
∵S△AEF=AE•AF=x(a﹣x)=﹣(x﹣a)2+a2,
∴当x=a时,S△AEF有最大值a2,
又∵S△ABC=×a2=a2,
∴S△AEF≤S△ABC.
故②正确;
EF2=AE2+AF2=x2+(a﹣x)2=2(x﹣a)2+a2,
∴当x=a时,EF2取得最小值a2,
∴EF≥a(等号当且仅当x=a时成立),
而AD=a,∴EF≥AD.
故④错误;
由①的证明知△AED≌△CFD,
∴S四边形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=AD2,
∵EF≥AD,
∴AD•EF≥AD2,
∴AD•EF>S四边形AEDF
故③错误;
当E、F分别为AB、AC的中点时,四边形AEDF为正方形,此时AD与EF互相平分.
故⑤正确.
综上所述,正确的有:①②⑤,共3个.
故选:C.
【点评】本题主要考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,图形的面积,函数的性质等知识,综合性较强,有一定难度.
4.(2021•宁波自主招生)如图,在△ABC中,∠BAC=90°,AB=8,AC=6,AD为△ABC的中线,点F在边AC上(不与端点重合),BF与AD交于点E,若AF=EF,则AE的长为( )
A.B.3C.D.4
【分析】过点D作DG∥AC交BF于点G,进而得到DG是△BFC的中位线,设AF=x,则CF=6﹣x,DG=(6﹣x),然后得证△EDG∽△EAF,再结合AF=EF得到DG=EG,从而利用相似三角形的性质列出方程,求得x的值,最后利用相似三角形的性质求得AE的长.
【解答】解:过点D作DG∥AC,交BF于点G,则∠EGD=∠EFA,
∵AD是△ABC的中线,
∴DG是△BFC的中位线,
设AF=x,则CF=6﹣x,EF=x,
∴DG=(6﹣x),
∵∠EGD=∠EFA,∠GED=∠FEA,
∴△EDG∽△EAF,
∴,
∵AF=EF,
∴EG=DG=(6﹣x),
∴FG=EG+EF=(6﹣x)+x=(6+x),
∴BF=6+x,
∵AB=8,AF=x,∠BAF=90°,
∴BF==,
∴=6+x,
解得:x=,
∴EG=,EF=,
∵AB=8,AC=6,∠BAC=90°,
∴BC=10,
∵AD是△ABC的中线,
∴AD=5,
∵△EDG∽△EAF,
∴,即,
解得:AE=.
故选:A.
【点评】本题考查相似三角形的判定与性质、勾股定理、三角形的中位线,解题的关键是过点D作DG∥AC交BF于点G构造中位线和相似三角形.
二.多选题(共1小题)
(多选)5.(2021•洪山区校级自主招生)在△ABC中,CA=CB,P是△ABC外一动点,满足∠CAP+∠CBP=180°,设∠CPA=α,则下列结论正确的有( )
A.∠CPA=∠CPB
B.设四边形ACBP的面积为S,则S≤AB•CP
C.若α=30°,BC=4,则PC的最大值为8
D.若α=60°,PA=4,PB=2,则PD的长度为
【分析】根据∠CAP+∠CBP=180°可知A,P,B,C四点共圆,根据圆周角定理,即可判断A选项;根据面积公式即可判断B选项;当PC为直径时,PC最大,α=30°时,解直角三角形即可判断C选项;过点B作BH⊥AP交AP的延长线于点H,过点D作DE⊥AP于点E,过点D作DF⊥PB于点F,根据S△APB==,列方程,即可求出PD的长,从而判断D选项即可.
【解答】解:∵∠CAP+∠CBP=180°,
∴A,P,B,C四点共圆,
∴∠CPA=∠CBA,∠CPB=∠CAB,
∵CA=CB,
∴∠CBA=∠CAB,
∴∠CPA=∠CPB,
故A选项符合题意;
∵S=AB•CP•sin∠ADC,
当∠ADC=90°时,sin∠ADC=1取得最大值,
∴S≤AB•CP,
故B选项符合题意;
当α=30°时,∠CPB=30°,
∵BC=4,
当PC为直径时,PC最大,此时∠PBC=90°,
∴PC=2BC=8,
∴PC的最大值为8,
故C选项符合题意;
过点B作BH⊥AP交AP的延长线于点H,过点D作DE⊥AP于点E,过点D作DF⊥PB于点F,如图所示:
当α=60°时,∠APC=∠BPC=60°,
∴DE=DF=PD•sin60°=PD,∠APB=120°,
∴∠BPH=60°,
∴BH=PB•sin60°=PB,
∵PA=4,PB=2,
∴S△APB==,
∴4×PD+2×PD=4×,
∴PD=,
故D选项符合题意,
故选:ABCD.
【点评】本题考查了四边形的综合,涉及等腰三角形,三角形的面积,四点共圆,解直角三角形,最值问题等,综合性较强,难度较大.
三.填空题(共3小题)
6.(2022•南陵县自主招生)如图,在△ABC中,∠BAC、∠BCA的平分线相交于点I,且BC=AI+AC,若∠ABC=35°,则∠BAC的度数为 70 度.
【分析】在BC上取CD=AC,连接BI、DI,然后利用边角边证明△ACI与△DCI全等,根据全等三角形对应边相等可得AI=DI,对应角相等可得∠CAI=∠CDI,再根据BC=AI+AC求出AI=BD,从而可得BD=DI,然后根据等角对等边的性质以及三角形的任意一个外角等于与它不相邻的两个内角的和可得∠CDI=2∠DBI,再根据角平分线的定义即可求出∠CDI=∠ABC,又∠BAC=2∠CAI,代入数据进行计算即可求解.
【解答】解:如图,在BC上取CD=AC,连接BI、DI,
∵CI平分∠ACB,
∴∠ACI=∠BCI,
在△ACI与△DCI中,
,
∴△ACI≌△DCI(SAS),
∴AI=DI,∠CAI=∠CDI,
∵BC=AI+AC,
∴BD=AI,
∴BD=DI,
∴∠IBD=∠BID,
∴∠CDI=∠IBD+∠BID=2∠IBD,
又∵AI、CI分别是∠BAC、∠ACB的平分线,
∴BI是∠ABC的平分线,
∴∠ABC=2∠IBD,∠BAC=2∠CAI,
∴∠CDI=∠ABC,
∴∠BAC=2∠CAI=2∠CDI=2∠ABC,
∵∠B=35°,
∴∠BAC=35°×2=70°,
故答案为:70.
【点评】本题考查了全等三角形的判定和性质,角平分线的定义,利用“割补法”作辅助线构造全等三角形以便于利用条件“BC=AI+AC”是解决本题的关键,也是难点.
7.(2021•武进区校级自主招生)如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积为24cm2,则AC长是 cm.
【分析】先根据四边形内角和定理判断出∠2+∠B=180°,再延长至点E,使DE=BC,连接AE,由全等三角形的判定定理得出△ABC≌△ADE,故可得出△ACE是直角三角形,再根据四边形ABCD的面积为24cm2即可得出结论.
【解答】解:延长CD至点E,使DE=BC,连接AE,
∵∠BAD=∠BCD=90°,
∴∠2+∠B=180°,
∵∠1+∠2=180°,∠2+∠B=180°,
∴∠1=∠B,
在△ABC与△ADE中,
∵,
∴△ABC≌△ADE(SAS),
∴∠EAD=∠BAC,AC=AE,S△AEC=S四边形ABCD
∵∠BAD=90°,
∴∠EAC=90°,
∴△ACE是等腰直角三角形,
∵四边形ABCD的面积为24cm2,
∴AC2=24,解得AC=4(cm)或﹣4,
∵AC为正数,
∴AC=4(cm).
故答案为:4.
【点评】本题考查的是全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形及等腰直角三角形,再根据三角形的面积公式进行解答即可.
8.(2021•渝中区校级自主招生)如图,在△ABC中,BE平分∠ABC交AC于点E,点D在BC上,连接AD交BE于点H,且∠DAB=∠C,BH=BD,过点H作HF∥BC交AC于点F,BG⊥AD交AC于点G,若AE=6,EF=2,则GF= .
【分析】延长HF、BG交于点P,利用角平分线及相似三角形的判定与性质可得∠ADB=∠CAB,再三次运用相似三角形的判定与性质可得BD=BH=9,设BP与DH交于点M,过点H作HQ∥PG交EF于Q,根据角平分线定义及相似三角形的性质可得在,最后根据ASA得△PFG≌△HFQ,由全等三角形的性质可得答案.
【解答】解:如图:延长HF、BG交于点P,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠DAB=∠C,∠DBA=∠ABC,
∴△ABD∽△CAB,
∴∠ADB=∠CAB,
∵BD=BH,
∴∠CAB=∠ADB=∠BHD=∠EHA,
∴△EHA∽△EAB,
∴∠EAH=∠EBA=∠CBE,
∴△EAH~DBH,
∵HF∥BC,
∴∠EHF=∠EBC=∠EAH,
∴△FEH∽△FHA,
∴=,=,
∴FH==4,
EH=•HA=×6=3,
∵∠EBA=∠EAH,
∴△EAH∽△EBA,
∴=,
∴EB==12,
∴BH=EB﹣EH=9,
∴BD=BH=9,
设BP与DH交于点M,
∵HP∥BD,
∴∠HPM=∠DBM,∠PHM=∠BDM,
∴△HPM∽△DBM,
∴=,
∵BD=BH,BM⊥DH,
∴BM平分HD,
∴==1,HP=BD=9,
∴PF=HP﹣HF=4,
过点H作HQ∥PG交EF于Q,
∴∠QHF=∠EPG=∠PBD=∠HBD=∠EHF,
∴HQ是△EHF内角∠EHF的角平分线,
∴存在,
∴FQ==,
∵,
∴△PFG≌△HFQ(ASA),
∴GF=FQ=.
故答案为:.
【点评】此题考查的是全等三角形的判定与性质、相似三角形的判定与性质、角平分线的定义等知识,合理作辅助线构造相似三角形是解决此题关键.
四.解答题(共6小题)
9.(2022•徐汇区校级自主招生)斜边和斜边上的高分别对应相等的两个直角三角形是否全等?判断并给出理由.
【分析】根据全等三角形的判定定理进行判断即可.
【解答】解:全等,理由如下:
证明:设点O,O′分别为AB,A′B′的中点,则CO=C′O′,
∵CD⊥AB于D,C'D'⊥A'B'于D',
∴∠CDB=∠C′D′B′=90°,
∴Rt△CDO≌Rt△C′D′O′(HL),
∴∠COD=∠C'O'D',
∵CO=BO,C′O′=B′O′,
∴∠OCB=∠B,∠O′C′B′=∠B′,
∴∠B=(180°﹣∠COB),∠B'=(180°﹣∠C′O′B′),
∴∠B=∠B',
∴△ABC≌△A′B′C′(AAS),
【点评】本题考查的是直角全等三角形的判定,掌握全等三角形的判定定理是解题的关键.
10.(2022•相城区校级自主招生)如图,等边△ABC内接于⊙O,P是上任一点(点P不与点A、B重合),连接AP、BP、CP,CP与AB交于点D,过点C作CM∥BP交PA的延长线于点M.
(1)求证:△ACM≌△BCP;
(2)若PA=1,PB=2.求⊙O的半径.
【分析】(1)证明∠M=∠BPC,∠MAC=∠PBC,AC=BC,即可证明△ACM≌△BCP(AAS);
(2)过点B作BQ⊥AP,交AP的延长线于点Q,过点A作AN⊥BC于点N,连接OB,求得∠PBQ=30°,得到PQ=PB=1,根据勾股定理得到BQ=,AN=,根据勾股定理即可得到结论.
【解答】(1)证明:∵四边形APBC是⊙O的内接四边形,
∴∠MAC=∠PBC,∠ACB+∠APB=180°;
∵CM∥BP,
∴∠M+∠APB=180°,
∴∠M=∠ACB;
又∵△ABC是等边三角形,
∴∠ACB=∠BAC=60°,AC=BC;而∠BPC=∠BAC=60°,
∴∠M=∠BPC;
在△ACM与△BCP中,
,
∴△ACM≌△BCP(AAS);
(2)解:过点B作BQ⊥AP,交AP的延长线于点Q,过点A作AN⊥BC于点N,连接OB,
∵∠APC=∠BPC=60°,
∴∠BPQ=60°,
∴∠PBQ=30°,
∴PQ=PB=1,
在Rt△BPQ中,BQ==,
在Rt△AQB中,AB===,
∵△ABC为等边三角形,
∴AN经过圆心O,
∴BN=AB=,
∴AN==,
在Rt△BON中,设BO=r,则ON=﹣r,
∴()2+(﹣r)2=r2,
解得:r=.
即⊙O的半径为.
【点评】本题考查了圆周角定理、等边三角形的判定和性质、三角形的外接圆与外心,全等三角形的判定和性质,平行线的性质,正确地作出辅助线是解题的关键.
11.(2021•镜湖区校级自主招生)如图凸四边形ABCD,AB=AC=BD+CD,∠ABD=60°.求∠ACD的度数.
【分析】延长BD到点E,使ED=CD,连接AE,先证明△ABE是等边三角形,得AB=AC=AE,再证明△ACD≌△AED,则∠ACD=∠E=60°.
【解答】解:如图,延长BD到点E,使ED=CD,连接AE,
∵AB=BD+CD,BD+CD=BD+ED=BE,
∴AB=BE,
∵∠ABD=60°,
∴△ABE是等边三角形,
∴AB=AC=AE,∠E=60°,
在△ACD和△AED中,
,
∴△ACD≌△AED(SSS),
∴∠ACD=∠E=60°.
【点评】此题重点考查等边三角形的判定与性质、全等三角形的判定与性质,正确地作出所需要的辅助线是解题的关键.
12.(2022•瓯海区校级自主招生)如图所示,在△ABC中,∠ABC=90°,D,G是边CA上的两点,连接BD,BG.过点A,G分别作BD的垂线,垂足分别为E,F,连接CF.若BE=EF,求证:∠ABG=∠DFC.
【分析】设AE、BG交于点I,作GH⊥AB于点H,连接HI,由AE⊥BD,GF⊥BD证明AE∥GF,则==1,BI=IG,BG=2BI,由S△ABG=2S△ABI得AB•HG=2×AI•BF,则AB•HG=AI•BF,由△AHG∽△ABC得=,则AB•HG=AH•BC,所以AH•BC=AI•BF,变形为=,而∠HAI=∠FBC=90°﹣∠ABE,所以△HAI∽△FBC,则∠AHI=∠BFC,所以∠IHB=∠DFC,再由IH=IB=BG得∠IHB=∠ABG,所以∠ABG=∠DFC.
【解答】证明:如图,设AE、BG交于点I,作GH⊥AB于点H,连接HI,
∵AE⊥BD,GF⊥BD,BE=EF,
∴AE∥GF,BE=BF,∠AEB=90°,
∴==1,
∴BI=IG,BG=2BI,
∴S△ABG=2S△ABI,
∴AB•HG=2×AI•BF,
∴AB•HG=AI•BF,
∵∠AHG=∠ABC=90°,∠HAG=∠BAC,
∴△AHG∽△ABC,
∴=,
∵AB•HG=AH•BC,
∴AH•BC=AI•BF,
∴=,
∵∠HAI=∠FBC=90°﹣∠ABE,
∴△HAI∽△FBC,
∴∠AHI=∠BFC,
∴180°﹣∠AHI=180°﹣∠BFC,
∴∠IHB=∠DFC,
∵∠BHG=90°,BI=IG,
∴IH=IB=BG,
∴∠IHB=∠ABG,
∴∠ABG=∠DFC.
【点评】此题重点考查平行线分线段成比例定理、相似三角形的判定与性质、同角的余角相等、根据面积等式证明线段的乘积相等、直角三角形斜边上的中线等于斜边的一半等知识与方法,正确地作出所需要的辅助线是解题的关键.
13.(2021•成都自主招生)已知:如图,在▱ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
【分析】(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等;
(2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=AB,CF=CD.
∴AE=CF.
在△AED和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)解:当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴▱四边形AGBD是矩形.
【点评】本题主要考查了平行四边形的基本性质和矩形的判定及全等三角形的判定.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.三角形全等的判定条件:SSS,SAS,AAS,ASA.
14.(2021•武进区校级自主招生)如图,△ABC是等腰直角三角形,CA=CB,点N在线段AB上(与A、B不重合),点M在射线BA上,且∠NCM=45°.
求证:MN2=AM2+BN2.
【分析】方法一:作点A关于直线MC的对称点D,连结DA、DM、DC,DN,则△MDC≌△MAC.然后证明△DCN≌△BCN(SAS),再利用勾股定理即可解决问题;方法二:如图,△CBN沿CN翻折得△CDN,则△DCN≌△BCN.然后证明△DCM≌△ACM(SAS),再利用勾股定理即可解决问题.
【解答】证明:方法一:如图,作点A关于直线MC的对称点D,连结DA、DM、DC,DN,则△MDC≌△MAC.
∵△ABC是等腰直角三角形,CA=CB,且∠NCM=45°,
∴∠DCN=∠DCM+∠MCA+∠ACN=∠DCM+45°,∠BCN=∠BCA﹣∠NCA=90°﹣(45°﹣∠MCA)=45°+∠MCA=45°+∠DCM.
∴∠DCN=∠BCN.
又CD=CA=CB,
在△DCN和△BCN中.
,
∴△DCN≌△BCN(SAS),
∴ND=NB,∠CDN=∠CBN=45°.
∵△MDC≌△MAC,
∴∠CDM=∠CAM=180°﹣∠CAB=180°﹣45°=135°.
∴∠MDN=∠MDC﹣∠NDC=135°﹣45°=90°.
∴MD⊥DN.
∵MD=MA,
∴MN2=DM2+DN2=AM2+BN2.
方法二:如图,△CBN沿CN翻折得△CDN,连接DM,则△DCN≌△BCN.
∴CD=CB=CA,DN=BN,∠CDN=∠CBN=45°,∠DCN=∠BCN.
∵∠NCM=45°,
∴∠DCM=∠DCN﹣∠MCN=∠BCN﹣45°=90°﹣∠ACN﹣45°=45°﹣∠ACN=∠ACM.
又CD=CA,CM=CM.
在△DCM和△ACM中.
,
∴△DCM≌△ACM(SAS),
∴MA=MD,∠CDM=∠CAM=135°,∠MDN=∠CDM﹣∠NDC=90°.
∴MN2=DM2+DN2=AM2+BN2.
【点评】本题考查了全等三角形的判定与性质,勾股定理,等腰直角三角形的性质,解决本题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
相关试卷
这是一份中考数学二轮复习冲刺第12讲 勾股定理及其逆定理(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版),文件包含中考数学二轮复习冲刺第12讲勾股定理及其逆定理知识精讲+真题练+模拟练+自招练原卷版doc、中考数学二轮复习冲刺第12讲勾股定理及其逆定理知识精讲+真题练+模拟练+自招练解析版doc等2份试卷配套教学资源,其中试卷共65页, 欢迎下载使用。
这是一份中考数学二轮复习冲刺第08讲 二次函数(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版),文件包含中考数学二轮复习冲刺第08讲二次函数知识精讲+真题练+模拟练+自招练原卷版doc、中考数学二轮复习冲刺第08讲二次函数知识精讲+真题练+模拟练+自招练解析版doc等2份试卷配套教学资源,其中试卷共173页, 欢迎下载使用。
这是一份中考数学二轮复习冲刺第07讲 平面直角坐标系与一次函数、反比例函数(知识精讲+真题练+模拟练+自招练)(2份打包,原卷版+解析版),文件包含中考数学二轮复习冲刺第07讲平面直角坐标系与一次函数反比例函数知识精讲+真题练+模拟练+自招练原卷版doc、中考数学二轮复习冲刺第07讲平面直角坐标系与一次函数反比例函数知识精讲+真题练+模拟练+自招练解析版doc等2份试卷配套教学资源,其中试卷共164页, 欢迎下载使用。









