中考数学二轮复习冲刺第15讲 圆的有关概念、性质与圆有关的位置关系（知识精讲+真题练+模拟练+自招练）（2份打包，原卷版+解析版）

这是一份中考数学二轮复习冲刺第15讲 圆的有关概念、性质与圆有关的位置关系（知识精讲+真题练+模拟练+自招练）（2份打包，原卷版+解析版），文件包含中考数学二轮复习冲刺第15讲圆的有关概念性质与圆有关的位置关系知识精讲+真题练+模拟练+自招练原卷版doc、中考数学二轮复习冲刺第15讲圆的有关概念性质与圆有关的位置关系知识精讲+真题练+模拟练+自招练解析版doc等2份试卷配套教学资源，其中试卷共111页， 欢迎下载使用。
【考纲要求】
1. 圆的基本性质和位置关系是中考考查的重点，但圆中复杂证明及两圆位置关系中证明会有下降趋势，不会有太复杂的大题出现；
2.中考试题中将更侧重于具体问题中考查圆的定义及点与圆的位置关系，对应用、创新、开放探究型题目，会根据当前的政治形势、新闻背景和实际生活去命题，进一步体现数学来源于生活，又应用于生活．
【知识导图】
【考点梳理】
考点一、圆的有关概念及性质
1．圆的有关概念
圆、圆心、半径、等圆；
弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧；
三角形的外接圆、三角形的内切圆、三角形的外心、三角形的内心、圆心角、圆周角．
2．圆的对称性
圆是轴对称图形，任何一条直径所在直线都是它的对称轴，圆有无数条对称轴；
圆是以圆心为对称中心的中心对称图形；
圆具有旋转不变性．
3．圆的确定
不在同一直线上的三个点确定一个圆．
4．垂直于弦的直径
垂径定理 垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
推论 平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．
要点诠释：在图中(1)直径CD，(2)CD⊥AB，(3)AM＝MB，(4)，(5)．若上述5个条件有2个成立，则另外3个也成立．因此，垂径定理也称“五二三定理”．即知二推三．
注意：(1)(3)作条件时，应限制AB不能为直径．

5．圆心角、弧、弦之间的关系
定理 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．
推论 在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量也相等．
6．圆周角
圆周角定理 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
推论1 在同圆或等圆中，相等的圆周角所对的弧也相等．
推论2 半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径．
考点二、与圆有关的位置关系
1．点和圆的位置关系
设⊙O的半径为r，点P到圆心的距离OP＝d，则有：
点P在圆外d＞r；
点P在圆上d＝r；
点P在圆内d＜r．
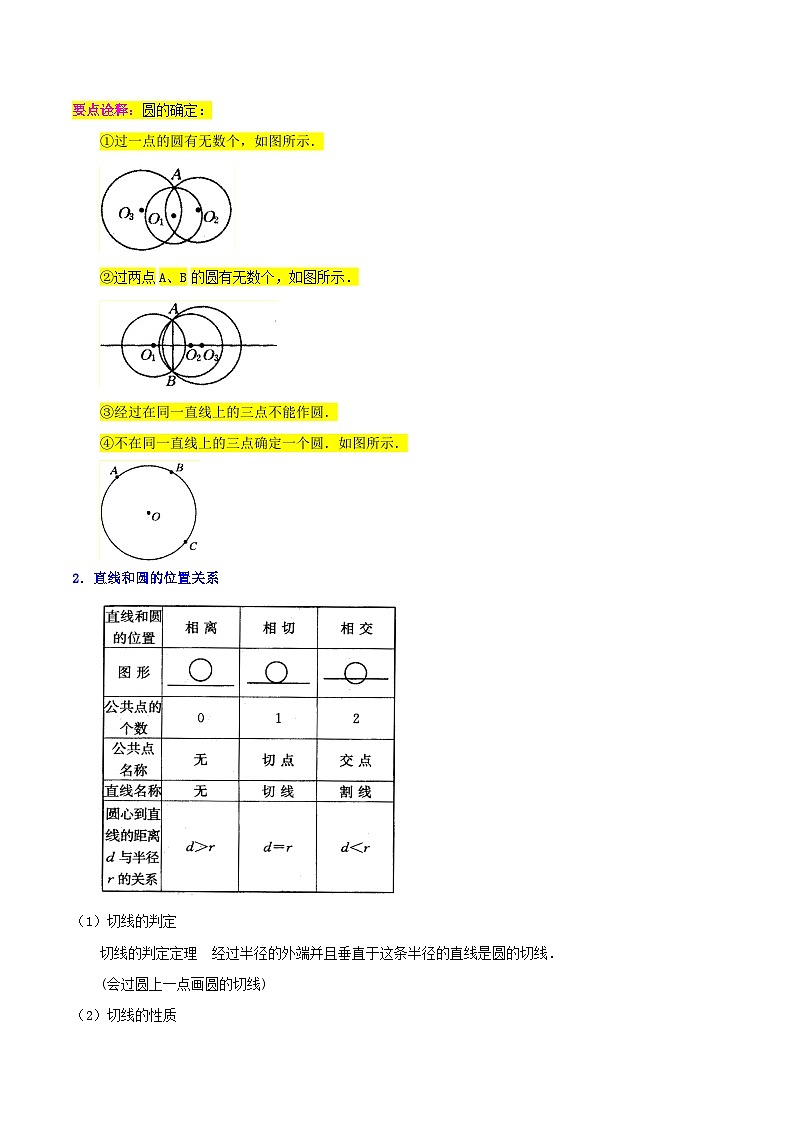
要点诠释：圆的确定：
①过一点的圆有无数个，如图所示．
②过两点A、B的圆有无数个，如图所示．
③经过在同一直线上的三点不能作圆．
④不在同一直线上的三点确定一个圆．如图所示．
2．直线和圆的位置关系
（1）切线的判定
切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线．
(会过圆上一点画圆的切线)
（2）切线的性质
切线的性质定理 圆的切线垂直于过切点的半径．
（3）切线长和切线长定理
切线长 经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长．
切线长定理 从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．
3．圆和圆的位置关系
(1)基本概念
两圆相离、相切、外离、外切、相交、内切、内含的定义．
(2)请看下表：
要点诠释：
①相切包括内切和外切，相离包括外离和内含．其中相切和相交是重点．
②同心圆是内含的特殊情况．
③圆与圆的位置关系可以从两个圆的相对运动来理解．
④“R-r”时，要特别注意，R＞r．
【典型例题】
题型一、圆的性质及垂径定理的应用
例1．已知：如图所示，在⊙O中，弦AB的中点为C，过点C的半径为OD．
(1)若AB＝，OC＝1，求CD的长；
(2)若半径OD＝R，∠AOB＝120°，求CD的长.
【思路点拨】
如图所示，一般的，若∠AOB＝2n°，OD⊥AB于C，OA＝R，OC＝h，
则AB＝2R·sin n°＝2n·tan n°＝；CD＝R－h；的长．
【答案与解析】
解：∵半径OD经过弦AB的中点C，
∴半径OD⊥AB．
(1)∵AB＝，AC＝BC＝．
∵OC＝1，由勾股定理得OA＝2．
∴CD＝OD－OC＝OA－OC＝1，
即CD＝1.
(2)∵OD⊥AB，OA＝OB，
∴∠AOD＝∠BOD．
∴∠AOB＝120°，∴∠AOC＝60°．
∵OC＝OA·cs∠AOC＝OA·cs60°＝，
∴．
【总结升华】
圆的半径、弦长的一半、弦心距三条线段组成一个直角三角形，其中一个锐角为弦所对圆心角的一半，可充分利用它们的关系解决有关垂径定理的计算问题．
【变式】在足球比赛场上，甲、乙两名队员互相配合向对方球门进攻，当甲带球冲到A点时，乙已跟随冲到B点(如图所示)，此时甲是自己直接射门好还是迅速将球回传给乙，让乙射门好呢?(不考虑其他因素)
【答案】
解：过M、N、B三点作圆，显然A点在圆外，
设MA交圆于C，则∠MAN＜∠MCN．
而∠MCN＝∠MBN，∴∠MAN＜∠MBN．
因此在B点射门较好．
即甲应迅速将球回传给乙，让乙射门．
例2．已知AB是⊙O的直径，C是圆周上的动点，P是弧AC的中点．
（1）如图1，求证：OP∥BC；
（2）如图2，PC交AB于D，当△ODC是等腰三角形时，求∠A的度数．
【思路点拨】
（1）连结AC，延长PO交AC于H，如图1，由P是弧AC的中点，根据垂径定理得PH⊥AC，再根据圆周角定理，由AB是⊙O的直径得∠ACB=90°，然后根据OP∥BC；
（2）如图2，根据圆心角、弧、弦的关系，以及三角形内角和等推论证来求得∠A的度数.
【答案与解析】
（1）证明：连结AC，延长PO交AC于H，如图1，
∵P是弧AB的中点，
∴PH⊥AC，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴BC⊥AC，
∴OP∥BC；
（2）解：如图2，
∵P是弧AC的中点，
∴PA=PC，
∴∠PAC=∠PCA，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠PAO=∠PCO，
当DO=DC，设∠DCO=x，则∠DOC=x，∠PAO=x，
∴∠OPC=∠OCP=x，∠PDO=2x，
∵∠OPA=∠PAO=x，
∴∠POD=2x，
在△POD中，x+2x+2x=180°，解得x=36°，
即∠PAO=36°，
当CO=CD，设∠DCO=x，则∠OPC=x，∠PAO=x，
∴∠POD=2x，
∴∠ODC=∠POD+∠OPC=3x，
∵CD=CO，
∴∠DOC=∠ODC=3x，
在△POC中，x+x+5x=180°，解得x=（）°，
即∠PAO=（）°．
综上所述，∠A的度数为36°或（）°．
【总结升华】本题考查了圆周角定理及其推论同时考查了等腰三角形的性质、垂径定理和三角形内角和定理．
【变式】如图，在Rt△ABC中，∠ACB=90°，AC=5，CB=12，AD是△ABC的角平分线，过A、C、D三点的圆与斜边AB交于点E，连接DE．
（1）求BE的长；
（2）求△ACD外接圆的半径．
【答案】
解：（1）∵∠ACB=90°，且∠ACB为圆O的圆周角（已知），
∴AD为圆O的直径（90°的圆周角所对的弦为圆的直径），
∴∠AED=90°（直径所对的圆周角为直角），
又AD是△ABC的角平分线（已知），
∴∠CAD=∠EAD（角平分线定义），
∴CD=DE（在同圆或等圆中，相等的圆周角所对的弦相等），
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴AC=AE（全等三角形的对应边相等）；
∵△ABC为直角三角形，且AC=5，CB=12，
∴根据勾股定理得：AB==13，
∴BE=13﹣AC=13﹣5=8；
（2）由（1）得到∠AED=90°，则有∠BED=90°，
设CD=DE=x，则DB=BC﹣CD=12﹣x，EB=AB﹣AE=AB﹣AC=13﹣5=8，
在Rt△BED中，根据勾股定理得：BD2=BE2+ED2，
即（12﹣x）2=x2+82，
解得：x=，
∴CD=，又AC=5，△ACD为直角三角形，
∴根据勾股定理得：AD==，
根据AD是△ACD外接圆直径，
∴△ACD外接圆的半径为：×=．
题型二、圆的切线判定与性质的应用
例3．如图所示，AB＝AC，O是BC的中点，⊙O与AB相切于点D，求证：AC与⊙O相切．
【思路点拨】AC与⊙O有无公共点在已知条件中没有说明，因此只能过点O向AC作垂线段OE，长等于⊙O的半径，则垂足E必在⊙O上，从而AC与⊙O相切．
【答案与解析】
证明：连接OD，作OE⊥AC，垂足为E，连结OA．
∵AB与⊙O相切于点D，∴OD⊥AB．
∵AB＝AC，OB＝OC，∴∠1＝∠2，
∴OE＝OD．
∵OD为⊙O半径，
∴AC与⊙O相切．

【总结升华】如果已知直线经过圆上一点，那么连半径，证垂直；如果已知直线与圆是否有公共点在条件中并没有给出，那么作垂直，证半径．
【变式】如图所示，在Rt△ABC中，∠C＝90°，BC＝a，AC＝b，AB＝c．求△ABC的内切圆的半径．
【答案】
解：设△ABC的内切圆与三边的切点分别为D、E、F，根据切线长定理可得：
AE＝AF，BF＝BD，CD＝CE，
而AE+CE＝b，CD+BD＝a，AF+BF＝c，
可求．
连接OE、OD，易证OE＝CE．
即直角三角形的内切圆半径．
例4．如图所示，已知：△ABC内接于⊙O，点D在OC的延长线上，，∠D＝30°．
(1)求证：AD是⊙O的切线；
(2)若AC＝6，求AD的长．

【思路点拨】
（1）连接OA，根据圆周角定理求出∠O的度数，根据三角形的内角和定理求出∠OAD，根据切线的判定推出即可；（2）得出等边三角形AOC，求出OA，根据勾股定理求出AD的长即可．
【答案与解析】
(1)证明：连接OA，
∵，∴∠B＝30°．
∵∠AOC＝2∠B，∴∠AOC＝60°．
∵∠D＝30°，
∴∠OAD＝180°－∠D－∠AOD＝90°．
∴AD是⊙O的切线．

(2)解：∵OA＝OC，∠AOC＝60°，
∴△AOC是等边三角形，∴OA＝AC＝6．
∵∠OAD＝90°，∠D＝30°，
∴AD＝AO＝．
【总结升华】
证明直线是圆的切线的方法：①有半径，证垂直；②有垂直，证半径．
【变式】如图所示，半径OA⊥OB，P是OB延长线上一点，PA交⊙O于D，过D作⊙O的切线交PO于C点，求证：PC＝CD．
【答案】
证明：连接OD．
∵CE切⊙O于D，∴OD⊥CE．
∴∠2+∠3＝90°．
∵OA⊥OB，∴∠P+∠A＝90°．
∵OD＝OA，∴∠3＝∠A．．∴∠P＝∠2．
又∵∠1＝∠2，∴∠P＝∠1．
∴PC＝CD．

题型三、切线的性质与等腰三角形、勾股定理综合运用
例5．已知AB是⊙O的直径，点P是AB延长线上的一个动点，过P作⊙O的切线，切点为C，∠APC的平分线交AC于点D，求∠CDP的度数.
【思路点拨】
连接OC，根据题意，可知OC⊥PC，∠CPD+∠DPA+∠A+∠ACO=90°，可推出∠DPA+∠A=45°，
即∠CDP=45°．
【答案与解析】
解：连接OC，
∵OC=OA，，PD平分∠APC，
∴∠CPD=∠DPA，∠A=∠ACO，
∵PC为⊙O的切线，
∴OC⊥PC，
∵∠CPD+∠DPA+∠A+∠ACO=90°，
∴∠DPA+∠A=45°，
即∠CDP=45°．
A
B
C
D
P
·
O
E
【总结升华】
本题主要考查切线的性质、等边三角形的性质、角平分线的性质、外角的性质，解题的关键在于做好辅助线构建直角三角形，求证∠CPD+∠DPA+∠A+∠ACO=90°，即可求出∠CDP=45°．
例6．如图所示，AB是⊙O的直径，AF是⊙O的弦，AE平分∠BAF，交⊙O于点E，过点E作直线ED⊥AF于点D，交AB的延长线于点C．
(1)求证：CD是⊙O的切线；
(2)若DE＝4，sinC＝，求AE的长．

【思路点拨】
构造半径、半弦、弦心距的直角三角形．
【答案与解析】
解：(1)证明：连接OE，BF，交于点G，
则BF⊥AF，BF∥CD．
∵OA＝OE，∴∠OAE＝∠OEA．
∵∠OAE＝∠FAE，∴∠OEA＝∠FAE．
∴OE∥AF，
∵AF⊥DE，∴OE⊥CD．
∴CD为⊙O的切线．

(2)解：∵ BF∥DE，OE∥AF，∠D＝90°，
∴四边形DEGF为矩形．
∴BF＝2GF＝2DE＝8．
∵BF∥CD，∴∠C＝∠ABF．
可求得OA＝OB＝5，OG＝3．
∴DF＝EG＝2，AF＝AB·sinC＝6．
∴AD＝8，AE＝．
【总结升华】
(1)通过挖掘图形的性质，将分散的条件sinC＝，DE＝4，集中到一个直角三角形中，使问题最终得到解决；
(2)本题第(2)问还可以适当改变后进行变式训练，如改为：若DF＝2，sinC＝，求AE的长；
(3)第(2)问还可以过O作OM⊥AF于M后得OM＝DE＝4，sin∠AOM＝sinC＝加以解决.
【中考过关真题练】
一．选择题（共8小题）
1．（2022•荆门）如图，CD是圆O的弦，直径AB⊥CD，垂足为E，若AB＝12，BE＝3，则四边形ACBD的面积为（ ）
A．36B．24C．18D．72
【分析】根据AB＝12，BE＝3，求出OE＝3，OC＝6，并利用勾股定理求出EC，根据垂径定理求出CD，即可求出四边形的面积．
【解答】解：如图，连接OC，
∵AB＝12，BE＝3，
∴OB＝OC＝6，OE＝3，
∵AB⊥CD，
在Rt△COE中，EC＝，
∴CD＝2CE＝6，
∴四边形ACBD的面积＝．
故选：A．
【点评】本题考查了垂径定理，解题的关键是熟练运用定理．垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
2．（2022•牡丹江）如图，BD是⊙O的直径，A，C在圆上，∠A＝50°，∠DBC的度数是（ ）
A．50°B．45°C．40°D．35°
【分析】由BD是⊙O的直径，可求得∠BCD＝90°，又由圆周角定理可得∠D＝∠A＝50°，继而求得答案．
【解答】解：∵BD是⊙O的直径，
∴∠BCD＝90°，
∵∠D＝∠A＝50°，
∴∠DBC＝90°﹣∠D＝40°．
故选：C．
【点评】此题考查了圆周角定理以及直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
3．（2022•淮安）如图，四边形ABCD是⊙O的内接四边形，若∠AOC＝160°，则∠ABC的度数是（ ）
A．80°B．100°C．140°D．160°
【分析】先根据圆周角定理求得∠D的度数，然后根据圆内接四边形的性质求出∠ABC的度数即可．
【解答】解：∵∠AOC＝160°，
∴∠ADC＝∠AOC＝80°，
∵四边形ABCD是⊙O的内接四边形，
∴∠ABC＝180°﹣∠ADC＝180°﹣80°＝100°，
故选：B．
【点评】此题考查的是圆内接四边形的性质及圆周角定理，比较简单，牢记有关定理是解答本题的关键．
4．（2022•西藏）如图，AB是⊙O的弦，OC⊥AB，垂足为C，OD∥AB，OC＝OD，则∠ABD的度数为（ ）
A．90°B．95°C．100°D．105°
【分析】连接OB，则OC＝OB，由OC⊥AB，则∠OBC＝30°，再由OD∥AB，即可求出答案．
【解答】解：如图：
连接OB，则OB＝OD，
∵OC＝OD，
∴OC＝OB，
∵OC⊥AB，
∴∠OBC＝30°，
∵OD∥AB，
∴∠BOD＝∠OBC＝30°，
∴∠OBD＝∠ODB＝75°，
∠ABD＝30°+75°＝105°．
故选：D．
【点评】本题考查了圆，平行线的性质，解直角三角形，等腰三角形的有关知识；正确作出辅助线、利用圆的半径相等是解题的关键．
5．（2022•株洲）如图所示，等边△ABC的顶点A在⊙O上，边AB、AC与⊙O分别交于点D、E，点F是劣弧上一点，且与D、E不重合，连接DF、EF，则∠DFE的度数为（ ）
A．115°B．118°C．120°D．125°
【分析】根据圆的内接四边形对角互补及等边△ABC的每一个内角是60°，求出∠EFD＝120°．
【解答】解：四边形EFDA是⊙O内接四边形，
∴∠EFD+∠A＝180°，
∵等边△ABC的顶点A在⊙O上，
∴∠A＝60°，
∴∠EFD＝120°，
故选：C．
【点评】本题考查了圆内接四边形的性质、等边三角形的性质，掌握两个性质定理的应用是解题关键．
6．（2022•镇江）如图，在等腰△ABC中，∠BAC＝120°，BC＝6，⊙O同时与边BA的延长线、射线AC相切，⊙O的半径为3．将△ABC绕点A按顺时针方向旋转α（0°＜α≤360°），B、C的对应点分别为B′、C′，在旋转的过程中边B′C′所在直线与⊙O相切的次数为（ ）
A．1B．2C．3D．4
【分析】设⊙O与边BA的延长线、射线AC分别相切于点T、点G，连接OA交⊙O于点L，连接OT，作AE⊥BC于点E，OH⊥BC于点H，先求得BE＝CE＝3，∠B＝∠ACB＝30°，则AE＝BE•tan30°＝3，再证明OA∥BC，则OH＝AE＝OT＝OL＝3，可证明直线BC与⊙O相切，再求得OA＝2OT＝6，则AL＝3，作AK⊥B′C′于点K，由旋转得AK＝AE＝3，∠AKB′＝∠AEB＝90°，直线B′C′与⊙O相切存在三种情况，一是△ABC绕点A旋转到点K与点L重合，二是△ABC绕点A旋转到B′C′∥OA，三是△ABC绕点A旋转到B′C′与BC重合，即旋转角α＝360°，分别加以说明即可．
【解答】解：如图1，由题意可知⊙O同时与边BA的延长线、射线AC相切，⊙O的半径为3，
设⊙O与边BA的延长线、射线AC分别相切于点T、点G，连接OA交⊙O于点L，连接OT，
∴AT⊥OT，OT＝3，
作AE⊥BC于点E，OH⊥BC于点H，则∠AEB＝90°，
∵AB＝AC，∠BAC＝120°，BC＝6，
∴BE＝CE＝BC＝3，∠B＝∠ACB＝（∠180﹣∠BAC）＝30°，
∴AE＝BE•tan30°＝3×＝3，
∵∠TAC＝180°﹣∠BAC＝60°，
∴∠OAG＝∠OAT＝∠TAC＝30°，
∴∠OAG＝∠ACB，
∴OA∥BC，
∴OH＝AE＝OT＝OL＝3，
∴直线BC与⊙O相切，
∵∠ATO＝90°，
∴OA＝2OT＝6，
∴AL＝3，
作AK⊥B′C′于点K，由旋转得AK＝AE＝3，∠AKB′＝∠AEB＝90°，
如图2，△ABC绕点A旋转到点K与点L重合，
∵∠OLB′＝180°﹣∠ALB′＝180°﹣∠AKB′＝90°，
∴B′C′⊥OL，
∵OL为⊙O的半径，
∴B′C′与⊙O相切；
如图3，△ABC绕点A旋转到B′C′∥OA，作OR⊥B′C′交C′B′的延长线于点R，
∵OR＝AK＝3，
∴B′C′与⊙O相切；
当△ABC绕点A旋转到B′C′与BC重合，即旋转角α＝360°，则B′C′与⊙O相切，
综上所述，在旋转的过程中边B′C′所在直线与⊙O相切3次，
故选：C．
【点评】此题重点考查等腰三角形的性质、圆的切线的判定、锐角三角函数以及数形结合与分类讨论数学思想的运用等知识与方法，画出图形并且正确地作出所需要的辅助线是解题的关键．
7．（2022•鄂尔多斯）实验学校的花坛形状如图所示，其中，等圆⊙O1与⊙O2的半径为3米，且⊙O1经过⊙O2的圆心O2．已知实线部分为此花坛的周长，则花坛的周长为（ ）
A．4π米B．6π米C．8π米D．12π米
【分析】连接AO1，AO2，BO1，BO2，O1O2，根据等边三角形的判定得出△AO1O2和△BO1O2是等边三角形，根据等边三角形的性质得出∠AO1O2＝∠AO2O1＝∠BO1O2＝∠BO2O1＝60°，求出优弧所对的圆心角的度数，再根据弧长公式求出即可．
【解答】解：连接AO1，AO2，BO1，BO2，O1O2，
∵等圆⊙O1与⊙O2的半径为3米，⊙O1经过⊙O2的圆心O2，
∴AO1＝AO2＝BO1＝BO2＝O1O2＝3米，
∴△AO1O2和△BO1O2是等边三角形，
∴∠AO1O2＝∠AO2O1＝∠BO1O2＝∠BO2O1＝60°，
∴优弧所对的圆心角的度数是360°﹣60°﹣60°＝240°，
∴花坛的周长为2×＝8π（米），
故选：C．
【点评】本题考查了相交两圆的性质，弧长公式，等边三角形的性质和判定等知识点，能求出圆心角的度数是解此题的关键．
8．（2022•德阳）如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D，与BC相交于点G，则下列结论：①∠BAD＝∠CAD；②若∠BAC＝60°，则∠BEC＝120°；③若点G为BC的中点，则∠BGD＝90°；④BD＝DE．其中一定正确的个数是（ ）
A．1B．2C．3D．4
【分析】利用三角形内心的性质得到∠BAD＝∠CAD，则可对①进行判断；直接利用三角形内心的性质对②进行判断；根据垂径定理则可对③进行判断；通过证明∠DEB＝∠DBE得到DB＝DE，则可对④进行判断．
【解答】解：∵E是△ABC的内心，
∴AD平分∠BAC，
∴∠BAD＝∠CAD，故①正确；
如图，连接BE，CE，
∵E是△ABC的内心，
∴∠EBC＝∠ABC，∠ECB＝ACB，
∵∠BAC＝60°，
∴∠ABC+∠ACB＝120°，
∴∠BEC＝180°﹣∠EBC﹣∠ECB＝180°﹣（∠ABC+∠ACB）＝120°，故②正确；
∵∠BAD＝∠CAD，
∴＝，
∴OD⊥BC，
∵点G为BC的中点，
∴G一定在OD上，
∴∠BGD＝90°，故③正确；
如图，连接BE，
∴BE平分∠ABC，
∴∠ABE＝∠CBE，
∵∠DBC＝∠DAC＝∠BAD，
∴∠DBC+∠EBC＝∠EBA+∠EAB，
∴∠DBE＝∠DEB，
∴DB＝DE，故④正确．
∴一定正确的①②③④，共4个．
故选：D．
【点评】本题考查了三角形的内切圆与内心，圆周角定理，三角形的外接圆与外心，解决本题的关键是掌握三角形的内心与外心．
二．填空题（共11小题）
9．（2022•宁夏）如图，在⊙O中，半径OC垂直弦AB于点D，若OB＝10，AB＝16，则csB＝ ．
【分析】根据垂径定理得BD＝AB＝8，再利用余弦的定义可得．
【解答】解：∵半径OC垂直弦AB于点D，
∴BD＝AB＝8，
∴csB＝＝，
故答案为：．
【点评】本题主要考查了垂径定理，三角函数的定义，熟练掌握垂径定理是解题的关键．
10．（2022•郴州）如图，点A．B，C在⊙O上，∠AOB＝62°，则∠ACB＝ 31 度．
【分析】由圆周角定理可求得答案．
【解答】解：∵∠AOB＝62°，
∴∠ACB＝∠AOB＝31°，
故答案为：31．
【点评】本题主要考查圆周角定理，掌握同弧所对的圆周角等于圆心角的一半是解题的关键．
11．（2022•长沙）如图，A、B、C是⊙O上的点，OC⊥AB，垂足为点D，且D为OC的中点，若OA＝7，则BC的长为 7 ．
【分析】根据已知条件证得△AOD≌△BCD（SAS），则BC＝OA＝7．
【解答】解：∵OA＝OC＝7，且D为OC的中点，
∴OD＝CD，
∵OC⊥AB，
∴∠ODA＝∠CDB＝90°，AD＝BD，
在△AOD和△BCD中，
∴△AOD≌△BCD（SAS），
∴BC＝OA＝7．
故答案为：7．
【点评】本题主要考查垂径定理和全等三角形的判定与性质，解题关键是熟知垂径定理内容．
12．（2022•锦州）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，∠ADC＝130°，连接AC，则∠BAC的度数为 40° ．
【分析】利用圆内接四边形的性质和∠ADC的度数求得∠B的度数，利用直径所对的圆周角是直角得到∠ACB＝90°，然后利用直角三角形的两个锐角互余计算即可．
【解答】解：∵四边形ABCD内接于⊙O，∠ADC＝130°，
∴∠B＝180°﹣∠ADC＝180°﹣130°＝50°，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠CAB＝90°﹣∠B＝90°﹣50°＝40°，
故答案为：40°．
【点评】本题考查了圆内接四边形的性质及圆周角定理的知识，解题的关键是了解圆内接四边形的对角互补．
13．（2022•雅安）如图，∠DCE是⊙O内接四边形ABCD的一个外角，若∠DCE＝72°，那么∠BOD的度数为 144° ．
【分析】根据邻补角的概念求出∠BCD，根据圆内接四边形的性质求出∠A，根据圆周角定理解答即可．
【解答】解：∵∠DCE＝72°，
∴∠BCD＝180°﹣∠DCE＝108°，
∵四边形ABCD内接于⊙O，
∴∠A＝180°﹣∠BCD＝72°，
由圆周角定理，得∠BOD＝2∠A＝144°，
故答案为：144°．
【点评】本题考查的是圆内接四边形的性质，掌握圆内接四边形的对角互补是解题的关键．
14．（2022•牡丹江）⊙O的直径CD＝10，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OC＝3：5，则AC的长为 4或2 ．
【分析】连接OA，由AB⊥CD，设OC＝5x，OM＝3x，根据CD＝10可得OC＝5，OM＝3，根据垂径定理得到AM＝4，然后分类讨论：当如图1时，CM＝8；当如图2时，CM＝2，再利用勾股定理分别计算即可．
【解答】解：连接OA，
∵OM：OC＝3：5，
设OC＝5x，OM＝3x，
则OD＝OC＝5x，
∵CD＝10，
∴OM＝3，OA＝OC＝5，
∵AB⊥CD，
∴AM＝BM＝AB，
在Rt△OAM中，OA＝5，
AM＝，
当如图1时，CM＝OC+OM＝5+3＝8，
在Rt△ACM中，AC＝；
当如图2时，CM＝OC﹣OM＝5﹣3＝2，
在Rt△ACM中，AC＝．
综上所述，AC的长为4或2．
故答案为：4或2．
【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．
15．（2022•徐州）如图，A、B、C点在圆O上，若∠ACB＝36°，则∠AOB＝ 72° ．
【分析】利用一条弧所对的圆周角等于它所对的圆心角的一半即可得出结论．
【解答】解：∵∠ACB＝∠AOB，∠ACB＝36°，
∴∠AOB＝2×∠ACB＝72°．
故答案为：72°．
【点评】本题主要考查了圆周角定理，利用一条弧所对的圆周角等于它所对的圆心角的一半解答是解题的关键．
16．（2022•泸州）如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝2，半径为1的⊙O在Rt△ABC内平移（⊙O可以与该三角形的边相切），则点A到⊙O上的点的距离的最大值为 2+1 ．
【分析】连接OE、OF，根据正切的定义求出∠ABC，根据切线长定理得到∠OBF＝30°，根据含30°角的直角三角形的性质、勾股定理计算，得到答案．
【解答】解：当⊙O与BC、BA都相切时，连接AO并延长交⊙O于点D，则AD为点A到⊙O上的点的距离的最大值，
设⊙O与BC、BA的切点分别为E、F，连接OE、OF，
则OE⊥BC，OF⊥AB，
∵AC＝6，BC＝2，
∴tan∠ABC＝＝，AB＝＝4，
∴∠ABC＝60°，
∴∠OBF＝30°，
∴BF＝＝，
∴AF＝AB﹣BF＝3，
∴OA＝＝2，
∴AD＝2+1，
故答案为：2+1．
【点评】本题考查的是切线的性质、直角三角形的性质、切线长定理，根据题意得出AD为点A到⊙O上的点的距离的最大值是解题的关键．
17．（2022•盐城）如图，AB、AC是⊙O的弦，过点A的切线交CB的延长线于点D，若∠BAD＝35°，则∠C＝ 35 °．
【分析】连接AO并延长交⊙O于点E，连接BE，根据切线的性质可得∠OAD＝90°，从而求出∠BAE＝55°，然后利用直径所对的圆周角是直角可得∠ABE＝90°，从而利用直角三角形的两个锐角互余可求出∠E的度数，最后根据同弧所对的圆周角相等，即可解答．
【解答】解：连接OA并延长交⊙O于点E，连接BE，
∵AD与⊙O相切于点A，
∴∠OAD＝90°，
∵∠BAD＝35°，
∴∠BAE＝∠OAD﹣∠BAD＝55°，
∵AE是⊙O的直径，
∴∠ABE＝90°，
∴∠E＝90°﹣∠BAE＝35°，
∴∠C＝∠E＝35°，
故答案为：35．
【点评】本题考查了切线的性质，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
18．（2022•黑龙江）如图，在⊙O中，AB是⊙O的弦，⊙O的半径为3cm．C为⊙O上一点，∠ACB＝60°，则AB的长为 3 cm．
【分析】连接AO并延长交⊙O于点D，根据直径所对的圆周角是直角可得∠ABD＝90°，再利用同弧所对的圆周角相等可求出∠ADB＝60°，然后在Rt△ABD中，利用锐角三角函数的定义进行计算即可解答．
【解答】解：连接AO并延长交⊙O于点D，
∵AD是⊙O的直径，
∴∠ABD＝90°，
∵∠ACB＝60°，
∴∠ADB＝∠ACB＝60°，
在Rt△ABD中，AD＝6cm，
∴AB＝AD•sin60°＝6×＝3（cm），
故答案为：3．
【点评】本题考查了三角形的外接圆与外心，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
19．（2022•湖北）如图，点P是⊙O上一点，AB是一条弦，点C是上一点，与点D关于AB对称，AD交⊙O于点E，CE与AB交于点F，且BD∥CE．给出下面四个结论：
①CD平分∠BCE；②BE＝BD；③AE2＝AF•AB；④BD为⊙O的切线．
其中所有正确结论的序号是 ①②④ ．
【分析】根据题意可得AB是CD的垂直平分线，从而可得AD＝AC，BD＝BC，再利用等腰三角形和平行线的性质可得CD平分∠BCE，即可判断①；根据圆内接四边形对角互补和平角定义可得∠DEB＝∠ACB，再利用SSS证明△ADB≌△ACB，然后利用全等三角形的性质可得∠ADB＝∠ACB，从而可得∠DEB＝∠ADB，即可判断②；根据等弧所对的圆周角相等可得∠AEF≠∠ABE，从而可得△AEF与△ABE不相似，即可判断③；连接OB，交EC于点H，利用①②的结论可得BE＝BC，从而可得＝，然后利用垂径定理可得∠OHE＝90°，最后利用平行线的性质可求出∠OBD＝90°，即可解答．
【解答】解：∵点C与点D关于AB对称，
∴AB是CD的垂直平分线，
∴AD＝AC，BD＝BC，
∴∠BCD＝∠BDC，
∵BD∥CE，
∴∠BDC＝∠DCE，
∴∠DCE＝∠BCD，
∴CD平分∠BCE；
故①正确；
∵四边形ACBE是⊙O的内接四边形，
∴∠ACB+∠AEB＝180°，
∵∠AEB+∠DEB＝180°，
∴∠DEB＝∠ACB，
∵AD＝AC，BD＝BC，AB＝AB，
∴△ADB≌△ACB（SSS），
∴∠ADB＝∠ACB，
∴∠DEB＝∠ADB，
∴BD＝BE，
故②正确；
∵AC≠AE，
∴≠，
∴∠AEF≠∠ABE，
∴△AEF与△ABE不相似，
故③不正确；
连接OB，交EC于点H，
∵BD＝BE，BD＝BC，
∴BE＝BC，
∴＝，
∴OB⊥CE，
∴∠OHE＝90°，
∵BD∥CE，
∴∠OHE＝∠OBD＝90°，
∵OB是⊙O的半径，
∴BD为⊙O的切线，
故④正确；
所以给出上面四个结论，其中所有正确结论的序号是：①②④，
故答案为：①②④．
【点评】本题考查了角平分线的定义，切线的判定，平行线的性质，相似三角形的判定与性质，圆周角定理，垂径定理，全等三角形的判定与性质，熟练掌握切线的判定，以及圆周角定理，垂径定理是解题的关键．
三．解答题（共8小题）
20．（2022•威海）如图，四边形ABCD是⊙O的内接四边形，连接AC，BD，延长CD至点E．
（1）若AB＝AC，求证：∠ADB＝∠ADE；
（2）若BC＝3，⊙O的半径为2，求sin∠BAC．
【分析】（1）根据圆内接四边形的性质以及等腰三角形的性质即可求证；
（2）连接CO并延长交⊙O于点F，连接BF，根据圆周角定理得出∠FBC＝90°，∠F＝∠BAC，解直角三角形即可得解．
【解答】（1）证明：∵四边形ABCD是⊙O的内接四边形，
∴∠ADE＝∠ABC，
∵AB＝AC，
∴∠ABC＝∠ACB，
∵∠ACB＝∠ADB，
∴∠ADB＝∠ADE；
（2）解：连接CO并延长交⊙O于点F，连接BF，
则∠FBC＝90°，
在Rt△BCF中，CF＝4，BC＝3，
∴sinF＝＝，
∵∠F＝∠BAC，
∴sin∠BAC＝．
【点评】此题考查了圆内接四边形的性质、圆周角定理，熟练掌握圆内接四边形的性质、圆周角定理是解题的关键．
21．（2022•黔东南州）（1）请在图1中作出△ABC的外接圆⊙O（尺规作图，保留作图痕迹，不写作法）；
（2）如图2，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是的中点，过点B的切线与AC的延长线交于点D．
①求证：BD⊥AD；
②若AC＝6，tan∠ABC＝，求⊙O的半径．
【分析】（1）利用尺规作图分别作出AB、AC的垂直平分线交于点O，以O为圆心、OA为半径作圆即可；
（2）①连接OB，根据切线的性质得到OB⊥BD，证明OB∥AD，根据平行线的性质证明结论；
②连接EC，根据圆周角定理得到∠AEC＝∠ABC，根据正切的定义求出EC，根据勾股定理求出AE，得到答案．
【解答】（1）解：如图1，⊙O即为△ABC的外接圆；
（2）①证明：如图2，连接OB，
∵BD是⊙O的切线，
∴OB⊥BD，
∵点B是的中点，
∴＝，
∴∠CAB＝∠EAB，
∵OA＝OB，
∴∠OBA＝∠EAB，
∴∠CAB＝∠OBA，
∴OB∥AD，
∴BD⊥AD；
②解：如图2，连接EC，
由圆周角定理得：∠AEC＝∠ABC，
∵tan∠ABC＝，
∴tan∠AEC＝，
∵AE是⊙O的直径，
∴∠ACE＝90°，
∴＝，
∵AC＝6，
∴EC＝8，
∴AE＝＝10，
∴⊙O的半径为5．
【点评】本题考查的是切线的性质、圆周角定理、解直角三角形，掌握圆的切线垂直于经过切点的半径是解题的关键．
22．（2022•攀枝花）如图，⊙O的直径AB垂直于弦DC于点F，点P在AB的延长线上，CP与⊙O相切于点C．
（1）求证：∠PCB＝∠PAD；
（2）若⊙O的直径为4，弦DC平分半径OB，求：图中阴影部分的面积．
【分析】（1）连接OC，根据切线的性质得到∠PCB+∠OCB＝90°，根据等腰三角形的性质得到∠OBC＝∠OCB，根据圆周角定理得到∠ADF＝∠OBC，等量代换证明结论；
（2）连接OD，根据直角三角形的性质求出∠ODF＝30°，根据三角形的面积公式得到S△CFB＝S△DFO，根据扇形面积公式计算，得到答案．
【解答】（1）证明：连接OC，
∵CP与⊙O相切，
∴OC⊥PC，
∴∠PCB+∠OCB＝90°，
∵AB⊥DC，
∴∠PAD+∠ADF＝90°，
∵OB＝OC，
∴∠OBC＝∠OCB，
由圆周角定理得：∠ADF＝∠OBC，
∴∠PCB＝∠PAD；
（2）解：连接OD，
在Rt△ODF中，OF＝OD，
则∠ODF＝30°，
∴∠DOF＝60°，
∵AB⊥DC，
∴DF＝FC，
∵BF＝OF，AB⊥DC，
∴S△CFB＝S△DFO，
∴S阴影部分＝S扇形BOD＝＝π．
【点评】本题考查的是切线的性质、扇形面积计算、垂径定理、圆周角定理，掌握圆的切线垂直于经过切点的半径是解题的关键．
23．（2022•阜新）如图，在Rt△ABC中，∠ACB＝90°，O是BC边上一点，以O为圆心，OB为半径的圆与AB相交于点D，连接CD，且CD＝AC．
（1）求证：CD是⊙O的切线；
（2）若∠A＝60°，AC＝2，求的长．
【分析】（1）连接OD．由等腰三角形的性质及圆的性质可得∠A＝∠ADC，∠B＝∠BDO．再根据余角性质及三角形的内角和定理可得∠ODC＝180°﹣（∠ADC+∠BDO）＝90°．最后由切线的判定定理可得结论；
（2）根据等边三角形的判定与性质可得∠DCO＝∠ACB﹣∠ACD＝30°．再由解直角三角形及三角形内角和定理可得∠BOD的度数，最后根据弧长公式可得答案．
【解答】（1）证明：连接OD．
∵AC＝CD，
∴∠A＝∠ADC．
∵OB＝OD，
∴∠B＝∠BDO．
∵∠ACB＝90°，
∴∠A+∠B＝90°．
∴∠ADC+∠BDO＝90°．
∴∠ODC＝180°﹣（∠ADC+∠BDO）＝90°．
又∵OD是⊙O的半径，
∴CD是⊙O的切线．
（2）解：∵AC＝CD＝，∠A＝60°，
∴△ACD是等边三角形．
∴∠ACD＝60°．
∴∠DCO＝∠ACB﹣∠ACD＝30°．
在Rt△OCD中，OD＝CDtan∠DCO＝tan30°＝2．
∵∠B＝90°﹣∠A＝30°，OB＝OD，
∴∠ODB＝∠B＝30°．
∴∠BOD＝180°﹣（∠B+∠BDO）＝120°．
∴的长＝．
【点评】此题考查的是切线的判定与性质、直角三角形的性质、弧长公式，正确作出辅助线是解决此题的关键．
24．（2022•六盘水）牂牁江“余月郎山，西陵晚渡”的风景描绘中有半个月亮挂在山上，月亮之上有个“齐天大圣”守护洞口的传说．真实情况是老王山上有个月亮洞，洞顶上经常有猴子爬来爬去，如图是月亮洞的截面示意图．
（1）科考队测量出月亮洞的洞宽CD约是28m，洞高AB约是12m，通过计算截面所在圆的半径可以解释月亮洞像半个月亮，求半径OC的长（结果精确到0.1m）；
（2）若∠COD＝162°，点M在上，求∠CMD的度数，并用数学知识解释为什么“齐天大圣”点M在洞顶上巡视时总能看清洞口CD的情况．
【分析】（1）设OA＝OC＝Rm，利用勾股定理求出R即可；
（2）补全⊙O，在CD的下方取一点N，连接CN，DN，CM，DM，利用圆周角定理，圆内接四边形的性质求解即可．
【解答】解：（1）设OA＝OC＝Rm，
∵OA⊥CD，
∴CB＝BD＝CD＝14m，
在Rt△COB中，OC2＝OB2+CB2，
∴R2＝142+（R﹣12）2，
∴R＝，
∴OC＝≈14.2m．
（2）补全⊙O，在CD的下方取一点N，连接CN，DN，CM，DM，
∵∠N＝∠COD＝81°，
∵∠CMD+∠N＝180°，
∴∠CMD＝99°．
∵∠CMD＝99°不变，是定值，
∴“齐天大圣”点M在洞顶上巡视时总能看清洞口CD的情况．
【点评】本题考查垂径定理的应用，圆周角定理，圆内接四边形的性质等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．
25．（2022•淮安）如图，△ABC是⊙O的内接三角形，∠ACB＝60°，AD经过圆心O交⊙O于点E，连接BD，∠ADB＝30°．
（1）判断直线BD与⊙O的位置关系，并说明理由；
（2）若AB＝4，求图中阴影部分的面积．
【分析】（1）连接BE，根据圆周角定理得到∠AEB＝∠C＝60°，连接OB，根据等边三角形的性质得到∠BOD＝60°，根据切线的判定定理即可得到结论；
（2）根据圆周角定理得到∠ABE＝90°，解直角三角形得到OB，根据扇形和三角形的面积公式即可得到结论．
【解答】解：（1）直线BD与⊙O相切，
理由：连接BE，
∵∠ACB＝60°，
∴∠AEB＝∠C＝60°，
连接OB，
∵OB＝OE，
∴△OBE是等边三角形，
∴∠BOD＝60°，
∵∠ADB＝30°，
∴∠OBD＝180°﹣60°﹣30°＝90°，
∴OB⊥BD，
∵OB是⊙O的半径，
∴直线BD与⊙O相切；
（2）∵AE是⊙O的直径，
∴∠ABE＝90°，
∵AB＝4，
∴sin∠AEB＝sin60°＝＝＝，
∴AE＝8，
∴OB＝4，
∴BD＝OB＝4，
∴图中阴影部分的面积＝S△OBD﹣S扇形BOE＝4×﹣＝8﹣．
【点评】本题考查了直线与圆的位置关系，等边三角形 的判定和性质，解直角三角形，扇形面积的计算，正确地作出辅助线是解题的关键．
26．（2022•宁夏）如图，以线段AB为直径作⊙O，交射线AC于点C，AD平分∠CAB交⊙O于点D，过点D作直线DE⊥AC于点E，交AB的延长线于点F．连接BD并延长交AC于点M．
（1）求证：直线DE是⊙O的切线；
（2）求证：AB＝AM；
（3）若ME＝1，∠F＝30°，求BF的长．
【分析】（1）连接OD，由∠ODA＝∠OAD＝∠DAC证明OD∥AC，得∠ODF＝∠AED＝90°，即可证明直线DE是⊙O的切线；
（2）由线段AB是⊙O的直径证明∠ADB＝90°，再根据等角的余角相等证明∠M＝∠ABM，则AB＝AM；
（3））由∠AEF＝90°，∠F＝30°证明∠BAM＝60°，则△ABM是等边三角形，所以∠M＝60°，则∠EDM＝30°，所以BD＝MD＝2ME＝2，再证明∠BDF＝∠F，得BF＝BD＝2．
【解答】（1）证明：连接OD，则OD＝OA，
∴∠ODA＝∠OAD，
∵AD平分∠CAB，
∴∠OAD＝∠DAC，
∴∠ODA＝∠DAC，
∴OD∥AC，
∵DE⊥AC，
∴∠ODF＝∠AED＝90°，
∵OD是⊙O的半径，且DE⊥OD，
∴直线DE是⊙O的切线．
（2）证明：∵线段AB是⊙O的直径，
∴∠ADB＝90°，
∴∠ADM＝180°﹣∠ADB＝90°，
∴∠M+∠DAM＝90°，∠ABM+∠DAB＝90°，
∵∠DAM＝∠DAB，
∴∠M＝∠ABM，
∴AB＝AM．
（3）解：∵∠AEF＝90°，∠F＝30°，
∴∠BAM＝60°，
∴△ABM是等边三角形，
∴∠M＝60°，
∵∠DEM＝90°，ME＝1，
∴∠EDM＝30°，
∴MD＝2ME＝2，
∴BD＝MD＝2，
∵∠BDF＝∠EDM＝30°，
∴∠BDF＝∠F，
∴BF＝BD＝2．
【点评】此题重点考查切线的判定、直径所对的圆周角是直角、等角的余角相等、等腰三角形的判定与性质、等边三角形的判定与性质、平行线的判定与性质、直角三角形中30°角所对的直角边等于斜边的一半等知识，正确地作出所需要的辅助线是解题的关键．
27．（2022•湖北）如图，正方形ABCD内接于⊙O，点E为AB的中点，连接CE交BD于点F，延长CE交⊙O于点G，连接BG．
（1）求证：FB2＝FE•FG；
（2）若AB＝6，求FB和EG的长．
【分析】（1）利用相似三角形的判定与性质解答即可；
（2）连接OE，利用平行线分线段成比例定理求得FB；利用相交弦定理求EG即可．
【解答】（1）证明：∵四边形ABCD是正方形，
∴AD＝BC，
∴．
∴∠DBA＝∠G．
∵∠EFB＝∠BFG，
∴△EFB∽△BFG，
∴，
∴FB2＝FE•FG；
（2）解：连接OE，如图，
∵AB＝AD＝6，∠A＝90°，
∴BD＝＝6．
∴OB＝BD＝3．
∵点E为AB的中点，
∴OE⊥AB，
∵四边形ABCD是正方形，
∴BC⊥AB，∠DBA＝45°，AB＝BC，
∴OE∥BC，OE＝BE＝AB．
∴．
∴，
∴，
∴BF＝2；
∵点E为AB的中点，
∴AE＝BE＝3，
∴EC＝＝3．
∵AE•BE＝EG•EC，
∴EG＝．
【点评】本题主要考查了正方形的性质，圆周角定理，垂径定理及其推论，相似三角形的判定与性质，平行线的性质，勾股定理，相交弦定理，灵活运用上述定理及性质是解题的关键．
【中考挑战满分模拟练】
一．选择题（共6小题）
1．（2023•汉阳区校级一模）如图，CD为⊙O直径，弦AB⊥CD于点E，CE＝1，AB＝6，则CD长为（ ）
A．10B．9C．8D．5
【分析】设⊙O的半径为R，则OE＝R﹣1，根据垂径定理求出AE＝BE＝3，∠AEO＝90°，在Rt△AEO中，由勾股定理得出方程R2＝（R﹣1）2+32，求出方程的解即可．
【解答】解：
设⊙O的半径为R，则OE＝R﹣1，
∵AB⊥CD，AB＝6，
∴AE＝BE＝3，∠AEO＝90°，
在Rt△AEO中，由勾股定理得：AO2＝AE2+OE2，
R2＝（R﹣1）2+32，
解得：R＝5，
即CD＝10，
故选：A．
【点评】本题考查了垂径定理，勾股定理的应用，解此题的关键是求出AE的长和得出关于R的方程，注意：垂直于弦的直径平分这条弦．
2．（2023•青岛一模）如图，四边形ABCD内接于⊙O，连接对角线AC与BD交于点E，且BD为⊙O的直径，已知∠BDC＝40°，∠AEB＝110°，则∠ABC＝（ ）
A．65°B．70°C．75°D．80°
【分析】根据圆周角定理得到∠BCD＝90°，根据直角三角形的性质求出∠DBC，计算即可．
【解答】解：∵BD为⊙O的直径，
∴∠BCD＝90°，
∴∠DBC＝90°﹣40°＝50°，
由圆周角定理得，∠BAC＝∠BDC＝40°，
∴∠ABD＝180°﹣∠AEB﹣∠BAC＝30°，
∴∠ABC＝∠ABD+∠DBC＝80°，
故选：D．
【点评】本题考查的是圆周角定理，掌握直径所对的圆周角为90°、直角三角形的性质是解题的关键．
3．（2023•雁塔区校级一模）如图，⊙O在△ABC三边上截得的弦长相等，即DE＝FG＝MN，∠A＝50°，则∠BOC＝（ ）
A．100°B．110°C．115°D．120°
【分析】过点O作OP⊥AB于点P，OQ⊥AC于点Q，OK⊥BC于点K，由于DE＝FG＝MN，所以弦的弦心距也相等，所以OB、OC是角平分线，可求出∠POQ，进而可求出∠BOC．
【解答】解：如图，过点O作OP⊥AB于点P，OQ⊥AC于点Q，OK⊥BC于点K，
∴∠APO＝∠AQO＝90°，
∵∠A＝50°，
∴∠POQ＝360°﹣90°﹣90°﹣50°＝130°，
∵DE＝FG＝MN，
∴OP＝OK＝OQ，
∴OB、OC平分∠ABC和∠ACB，
∴∠BOC＝＝115°．
故选：C．
【点评】本题主要考查垂径定理，解题关键是构造出辅助线——弦心距．
4．（2023•碑林区校级模拟）如图，△ABC是⊙O的内接三角形，∠B＝45°，AD⊥BC于点D，若BC＝4，AD＝3，则⊙O的半径长为（ ）
A．B．2C．D．
【分析】作⊙O的直径AE，连接BE，根据勾股定理求出AC，证明△ABE∽△ADC，根据相似三角形的性质列出比例式，把已知数据代入计算即可．
【解答】解：如图，作⊙O的直径AE，连接BE，
在Rt△ADB中，∠ABD＝90°，AD＝3，
则BD＝AD＝3，AB＝3，
∴DC＝BC﹣BD＝1，
∴AC＝＝，
∵AE是⊙O的直径，
∴∠ABE＝90°，
∴∠ABE＝∠ADC，
∵∠E＝∠C，
∴△ABE∽△ADC，
∴＝，即＝，
解得：AE＝2，
∴⊙O的半径长为，
故选：A．
【点评】本题考查的是三角形的外接圆与外心，掌握圆周角定理、相似三角形的判定定理是解题的关键．
5．（2023•庐江县模拟）如图，AB，AC分别是半圆O的直径和弦，AB＝5，AC＝4，D是上的一个动点，连接AD．过点C作CE⊥AD于E，连接BE，则BE的最小值是（ ）
A．2B．3C．2D．3
【分析】取AC中点M，连接MB，EM，BC，由勾股定理求出BC，MB的长，由直角三角形的性质求出ME的长，由ME+BE≥BM，即可解决问题．
【解答】解：取AC中点M，连接MB，EM，BC，
∵AB是半⊙O的直径，
∴∠ACB＝90°，
∴BC＝＝＝3，
∵MC＝AC＝×4＝2，
∴MB＝＝＝，
∵CE⊥AD，
∴∠AEC＝90°，
∴ME＝AC＝2，
∵ME+BE≥BM，
∴BE≥MB﹣ME＝﹣2，
∴BE的最小值是﹣2．
故选：A．
【点评】本题考查求线段的最小值，关键是掌握圆周角定理，勾股定理，直角三角形的性质．
6．（2023•宁波模拟）如图，四边形ABCD内接于⊙O，AB为直径，AD＝CD，过D作DE⊥AB于点E，交AC于点F，连结AC．DF＝5，．当点P为下面半圆弧的中点时，连接CP交BD于H，则AH的长为（ ）
A．B．C．D．12
【分析】连接AH，如图，根据直径所对的圆周角为直角可得∠ADB＝∠ACB＝90°，再运用同弧（等弧）所对的圆周角相等可得出∠DAC＝∠ABD，再利用同角的余角相等可推出∠ADE＝∠DAC，进而得出AF＝DF＝5，利用三角函数可求得EF＝3，由勾股定理可求得：AE＝4，AD＝4，再根据三角形的内心判定和性质可得出∠AHD＝45°，运用等腰直角三角形性质即可求得答案．
【解答】解：连接AH，如图，
∵AB为直径，
∴∠ADB＝∠ACB＝90°，
∵AD＝CD，
∴∠DAC＝∠DCA，
而∠DCA＝∠ABD，
∴∠DAC＝∠ABD，
∵DE⊥AB，
∴∠ABD+∠BDE＝90°，
而∠ADE+∠BDE＝90°，
∴∠ABD＝∠ADE，
∴∠ADE＝∠DAC，
∴AF＝DF＝5，
在Rt△AEF和Rt△ABC中，
∵sin∠CAB＝＝＝，
∴EF＝3，
∴AE＝＝4，DE＝5+3＝8，
∴AD＝＝4，
∵P为下面半圆弧的中点，
∴＝，
∴∠ACP＝∠BCP，
∴点H是△ABC的内心，
∴BH平分∠BAC，
∴∠BAH＝∠BAC，
∵∠ADB＝90°，
∴∠BAC+∠ABC＝90°，
∴∠AHD＝∠BAH+∠ABD＝（∠BAC+∠ABC）＝45°，
∵∠ADB＝90°，
∴△ADH是等腰直角三角形，
∴AH＝AD＝×4＝4．
故选：A．
【点评】本题考查了圆周角定理，三角形的内心，三角函数定义，等腰三角形和等腰直角三角形性质，勾股定理等，熟练掌握勾股定理、圆周角定理并作出合理的辅助线是解题的关键．
二．填空题（共6小题）
7．（2023•泸县校级一模）如图，AB是⊙O的弦，C是的中点，OC交AB于点D．若AB＝8cm，CD＝2cm，则⊙O的半径为 5 cm．
【分析】先根据圆心角、弧、弦的关系和垂径定理得出各线段之间的关系，再利用勾股定理求解出半径即可．
【解答】解：如图，连接OA，
∵C是的中点，
∴D是弦AB的中点，
∴OC⊥AB，AD＝BD＝4，
∵OA＝OC，CD＝2，
∴OD＝OC﹣CD＝OA﹣CD，
在Rt△OAD中，
OA2＝AD2+OD2，即OA2＝16+（OA﹣2）2，
解得OA＝5，
故答案为：5．
【点评】本题考查圆心角、弧、弦的关系及垂径定理的运用，做此类型题目通常需要结合圆心角、弦和三角形的相关知识来进行解答．
8．（2023•宁波模拟）圆内接四边形ABCD，两组对边的延长线分别相交于点E、F，且∠E＝40°，∠F＝60°，求∠A＝ 40 °．
【分析】根据圆内接四边形的性质得到∠BCD＝180°﹣∠A，根据三角形的外角的性质计算即可．
【解答】解：∵四边形ABCD是圆内接四边形，
∴∠BCD＝180°﹣∠A，
∵∠CBF＝∠A+∠E，∠DCB＝∠CBF+∠F，
∴180°﹣∠A＝∠A+∠E+∠F，即180°﹣∠A＝∠A+40°+60°，
解得∠A＝40°．
故答案为：40．
【点评】本题考查的是圆内接四边形的性质，掌握圆内接四边形的对角互补、圆内接四边形的任意一个外角等于它的内对角是解题的关键．
9．（2023•武汉模拟）如图，⊙O是△ABC的内切圆，∠C＝40°，则∠AOB的大小是 110° ．
【分析】利用三角形的内角和定理与角平分线的性质解答即可．
【解答】解：∵⊙O是△ABC的内切圆，
∴∠OAB＝，∠OBA＝，
∴∠AOB＝180°﹣（∠OAB+∠OBA）
＝180°﹣（+）
＝180°
＝+90°
＝+90°
＝110°．
故答案为：110°．
【点评】本题主要考查了三角形的内心与内切圆，熟练运用三角形的内角和定理与角平分线的性质是解题的关键．
10．（2023•定远县校级一模）如图，在Rt△ABC中，AB⊥BC、AB＝6，BC＝4，点P是△ABC内部的一个动点，连接PC，且满足∠PAB＝∠PBC，过点P作PD⊥BC交BC于点D．
（1）∠APB＝ 90° ；
（2）当线段CP最短时，△BCP的面积为 ．
【分析】（1）由∠ABP+∠PBC＝90°得到∠BAP+∠ABP＝90°，即可得到∠APB＝90°；
（2）首先证明点P在以AB为直径的⊙O上，连接OC与⊙O交于点P，此时PC最小，利用勾股定理求出OC即可得到＝，即可得到S△BCP＝S△OBC＝．
【解答】解：（1）∵∠ABC＝90°，
∴∠ABP+∠PBC＝90°，
∵∠PAB＝∠PBC，
∴∠BAP+∠ABP＝90°，
∴∠APB＝90°；
故答案为：90°；
（2）设AB的中点为O，连接OP，则OP＝OA＝OB（直角三角形斜边中线等于斜边一半），
∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小，
在Rt△BCO中，∠OBC＝90°，BC＝4，OB＝3，
∴OC＝＝5，
∴PC＝OC﹣OP＝5﹣3＝2．
∴＝，
∵S△OBC＝BC•OB＝×4×3＝6，
∴S△BCP＝S△OBC＝×6＝，
故答案为：．
【点评】本题考查点与圆位置关系、圆周角定理、最短问题等知识，解题的关键是确定点P位置，学会求圆外一点到圆的最小、最大距离，属于中考常考题型．
11．（2023•石家庄模拟）如图，在△ABC的外接圆⊙O中，AB＝2，，点E为AB的中点，则⊙O的直径为 ．
【分析】连接OA、OB，根据等腰三角形的性质得到AE＝BE＝1，∠AOE＝∠BOE＝∠ACB，根据正弦函数可求得半径，即可求解．
【解答】解：连接OA、OB，则OA＝OB，
∵点E为AB的中点，
∴AE＝BE＝1，∠AOE＝∠BOE＝∠ACB，
∵，
∴，
∴，
∴⊙O的直径为．
故答案为：．
【点评】本题考查了等腰三角形的性质，圆周角定理，正弦函数，解题的关键是灵活运用所学知识解决问题．
12．（2023•丰台区校级模拟）如图，PA，PB是⊙O的两条切线，切点分别为A，B，连接OA，AB，若∠OAB＝35°，则∠P＝ 70 °．
【分析】先根据等边对等角和三角形内角和定理求出∠AOB＝110°，再根据切线的性质得到∠OAP＝∠OBP＝90°，再根据四边形内角和定理求出∠P的度数即可．
【解答】解：∵OA＝OB，
∴∠OAB＝∠OBA＝35°，
∴∠AOB＝180°﹣∠OAB﹣∠OBA＝110°，
∵PA，PB是⊙O的两条切线，
∴∠OAP＝∠OBP＝90°，
∴∠P＝360°﹣∠AOB﹣∠OAP﹣∠OBP＝70°，
故答案为：70．
【点评】本题主要考查了切线的性质，等边对等角，三角形内角和定理，四边形内角和定理，熟知切线的性质是解题的关键．
三．解答题（共5小题）
13．（2023•定远县校级一模）已知⊙O中，AB是直径，AC是弦，∠BAC＝32°．
（1）如图1，连接BC，求∠ABC的度数；
（2）如图2，过点C作弦CD⊥AB，H为垂足，求∠BOD的度数．
【分析】（1）根据圆周角定理求解即可；
（2）根据圆周角定理求解即可．
【解答】解：（1）∵AB是直径，
∴∠ACB＝90°，
∴∠BAC+∠ABC＝90°，
∵∠BAC＝32°，
∴∠ABC＝58°；
（2）∵AB是直径，CD⊥AB，
∴＝，
∴∠BOD＝2∠BAC，
∵∠BAC＝32°，
∴∠BOD＝64°．
【点评】此题考查了圆周角定理，熟记圆周角定理是解题的关键．
14．（2023•丰台区校级模拟）圆管涵是公路路基排水中常用的涵洞结构类型，它不仅力学性能好，而且构造简单、施工方便．某水平放置的圆管涵圆柱形排水管道的截面是直径为1m的圆，如图所示，若水面宽AB＝0.8m，求水的最大深度．
【分析】过点O作OC⊥AB于点C，连接OA，根据垂径定理得到AC＝0.4，再在Rt△ACO中，根据勾股定理可求出OC，进而即可求解．
【解答】解：如图，作OC⊥AB于点C，连接OA，
∵∠ACO＝90°，，
∵AB＝0.8，
∴AC＝0.4，
在Rt△ACO中，根据勾股定理，得，
∴0.3+0.5＝0.8，
∴水的最大深度为0.8m．
【点评】此题主要考查了垂径定理的应用，以及勾股定理，熟练掌握定理是解题的关键．
15．（2023•西安一模）如图，AB为⊙O的直径，OD为⊙O的半径，⊙O的弦CD与AB相交于点F，⊙O的切线CE交AB的延长线于点E，EF＝EC．
（1）求证：OD垂直平分AB；
（2）若⊙O的半径长为3，且BF＝BE，求OF的长．
【分析】（1）连接OC，根据切线的性质可得∠OCF+∠ECF＝90°，然后根据等边对等角，等量代换求出∠ODF+∠OFD＝90°，证得OD⊥AB即可；
（2）设BF＝BE＝x，则EC＝EF＝2x，OE＝3+x，在Rt△OCE中，利用勾股定理构建方程求出x，然后根据OF＝OB﹣BF计算得出答案．
【解答】（1）证明：如图，连接OC，
∵CE切⊙O于点C，
∴OC⊥CE，
∴∠OCF+∠ECF＝90°，
∵OC＝OD，EF＝EC，
∴∠OCF＝∠ODF，∠ECF＝∠EFC，
又∵∠OFD＝∠EFC，
∴∠ODF+∠OFD＝90°，
∴∠DOF＝90°，
∴OD⊥AB，
∵OA＝OB，
∴OD垂直平分AB；
（2）解：设BF＝BE＝x，则EC＝EF＝2x，OE＝3+x，
在Rt△OCE中，OC2+CE2＝OE2，
∴32+（2x）2＝（3+x）2，
解得：x1＝2，x2＝0（舍去），
∴OF＝OB﹣BF＝3﹣2＝1．
【点评】本题考查了切线的性质，等腰三角形的性质，勾股定理以及解一元二次方程，熟知圆的切线垂直于经过切点的半径是解题的关键．
16．（2023•雁塔区校级二模）如图，⊙O与△ABC的边AB相切于点E，点O在边BC上，AB＝AC，AO交⊙O于点F，且AO⊥BC于点O．
（1）求证：AC是⊙O的切线；
（2）已知点H为⊙O上一点，，，⊙O的半径为1，求HF的长．
【分析】（1）作OK⊥AC，根据角平分线的性质证明K在圆上，即可证明AC是⊙O的切线；
（2）连接OH，通过证明△OEA≌△OKA得出∠EOF＝∠KOF，在Rt△AOE中根据已知条件求出sin∠AOE，再根据，得到∠AOK＝∠KOH，OM⊥FH，M为FH的中点，求出FM即可．
【解答】（1）证明：作OK⊥AC，K为垂足，
∵AB＝AC，AO⊥BC，
∴AO平分∠BAC，
∵AB与⊙O相切于点E，
∵OE⊥AB，OK⊥AC，
∴OE＝OK，
∴K在圆上，
∴AC是⊙O的切线；
（2）解：连接OH，
由（1）知，∠OEA＝∠OKA，
在Rt△OEA和Rt△OKA中，
，
∴Rt△OEA≌Rt△OKA（HL），
∴∠EOF＝∠KOF，
∴＝，
∵，
∴K为的中点，
设OK与FH相交于点M，
则OM⊥FH，且M为FH的中点，
∵OA＝，OE＝1，
∴AE＝＝，
∴sin∠AOE＝＝，
∴FM＝OF•sin∠FOM＝1×＝，
∴FH＝2FM＝．
【点评】本题考查了切线的判定和性质，以及角平分线性质的应用和圆的有关性质，解直角三角形等知识，判断M是FH的中点是解题关键．
17．（2023•雁塔区校级二模）如图，AB为⊙O的直径，弦CD⊥AB，垂足为点P，直线BF与AD延长线交于点F，且∠AFB＝∠ABC．
（1）求证：直线BF是⊙O的切线；
（2）若tan∠BCD＝，OP＝1，求线段BF的长．
【分析】（1）欲证明直线BF是⊙O的切线，只要证明AB⊥BF即可．
（2）连接OC，设OC＝OB＝x，则PB＝x﹣1，解直角三角形求得PC＝2（x﹣1），在Rt△OPC中，利用勾股定理求出OB＝，进而求得PD＝PC＝，AB＝，AP＝由△APD∽△ABF，＝，即可解决问题．
【解答】（1）证明：∵∠AFB＝∠ABC，∠ABC＝∠ADC，
∴∠AFB＝∠ADC，
∴CD∥BF，
∴∠APD＝∠ABF，
∵CD⊥AB，
∴AB⊥BF，
∴直线BF是⊙O的切线．
（2）解：连接OC，
∵CD⊥AB，
∴PD＝CD，
设OC＝OB＝x，
∴PB＝x﹣1，
∵tan∠BCD＝，
∴PC＝2（x﹣1），
在Rt△POC中，OC2＝PC2+OP2，
∴x2＝（2x﹣2）2+12，
解得x＝，x＝1（舍去），
∴OB＝，
∴PD＝PC＝，AB＝，AP＝
∵∠PAD＝∠BAF，∠APD＝∠ABF，
∴△APD∽△ABF，
∴＝，
∴＝，
∴BF＝．
【点评】本题考查切线的判定，垂径定理、勾股定理．相似三角形的判定和性质等知识，解题的关键是灵活运用这些知识解决问题，学会条件常用辅助线，属于中考常考题型．
【名校自招练】
一．选择题（共7小题）
1．（2022•南岸区自主招生）如图，在⊙O中，∠BOC＝80°，则∠A等于（ ）
A．50°B．20°C．30°D．40°
【分析】根据圆周角定理即可解决问题；
【解答】解：∵∠A＝∠BOC，∠BOC＝80°
∴∠A＝40°．
故选：D．
【点评】此题目考查了圆周角定理，属于中考基础题．
2．（2022•巴南区自主招生）如图，△ABC内接于⊙O，AB是⊙O的直径，BD是⊙O的切线，点B为切点，BD与线段AC的延长线相交于点D，若∠ABC＝65°，则∠D等于（ ）
A．65°B．55°C．45°D．35°
【分析】根据切线的性质得到AB⊥BD，则∠ABD＝90°，根据圆周角定理得到∠ACB＝90°，然后根据等角的余角相等得到∠D＝∠ABC．
【解答】解：∵BD是⊙O的切线，点B为切点，
∴AB⊥BD，
∴∠ABD＝90°，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∵∠A+∠ABC＝90°，
∵∠A+∠D＝90°，
∴∠D＝∠ABC＝65°．
故选：A．
【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．
3．（2022•北碚区自主招生）如图，AB是⊙O的切线，A为切点，OB交⊙O于点C，若⊙O的半径长为1，AB＝，则线段BC的长是（ ）
A．1B．C．2D．
【分析】连接OA，如图，先根据切线的性质得到∠BAO＝90°，则利用勾股定理可计算出OB＝2，然后计算OB﹣OC即可．
【解答】解：连接OA，如图，
∵AB是⊙O的切线，A为切点，
∴OA⊥AB，
∴∠BAO＝90°，
在Rt△OAB中，OB＝＝＝2，
∴BC＝OB﹣OC＝2﹣1＝1．
故选：A．
【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．
4．（2022•荣昌区自主招生）如图，AB是⊙O的切线，切点为B，CD是⊙O的直径，连接BD，BO，BC，若∠ABC＝50°，则∠D的度数是（ ）
A．45°B．50°C．55°D．60°
【分析】先根据切线的性质得到∠OBA＝90°，再根据圆周角定理得到∠CBD＝90°，则利用等角的余角相等得到∠OBD＝∠ABC＝50°，然后利用等腰三角形的性质得到∠D的度数．
【解答】解：∵AB是⊙O的切线，切点为B，
∴OB⊥AB，
∴∠OBA＝90°，
∵CD是⊙O的直径，
∴∠CBD＝90°，
∵∠OBD+∠OBC＝90°，∠ABC+∠OBC＝90°，
∴∠OBD＝∠ABC＝50°，
∵OB＝OD，
∴∠D＝∠OBD＝50°．
故选：B．
【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．
5．（2022•九龙坡区自主招生）如图，PA，PB分别与⊙O相切于A，B两点，Q是优弧上一点，若∠APB＝40°，则∠AQB的度数是（ ）
A．50°B．70°C．80°D．85°
【分析】连接OA、OB，如图，先根据切线的性质得OA⊥PA，OB⊥PB，再利用四边形的内角和计算出∠AOB＝140°，然后根据圆周角定理得到∠AQB的度数．
【解答】解：连接OA、OB，如图，
∵PA，PB分别与⊙O相切于A，B两点，
∴OA⊥PA，OB⊥PB，
∴∠OAP＝∠OBP＝90°，
∵∠AOB＝360°﹣90°﹣90°﹣∠P＝180°﹣40°＝140°，
∴∠AQB＝∠AOB＝70°．
故选：B．
【点评】本题看了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理．
6．（2022•渝北区自主招生）如图，矩形ABCD中，BC＝4，CD＝2，以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为（ ）
A．πB．π﹣2C．π+2D．π+4
【分析】连接OE交BD于F点，如图，根据切线的性质得到∠OEC＝90°，再证明四边形ABEO和四边形OECD为矩形，则OD＝OA＝BE＝2，∠DOE＝90°，接着证明△ODF≌△EBF得到S△ODF＝S△EBF，所以阴影部分的面积＝S扇形DOE，从而根据扇形的公式计算即可．
【解答】解：连接OE交BD于F点，如图，
∵以AD为直径的半圆O与BC相切于点E，
∴OE⊥BC，
∴∠OEC＝90°，
∵四边形ABCD为矩形，
∴∠OAB＝∠ABE＝∠C＝∠ODC＝90°，
∴四边形ABEO和四边形OECD为矩形，
∴OD＝OA＝BE＝2，∠DOE＝90°，
在△ODF和△EBF中，
，
∴△ODF≌△EBF（AAS），
∴S△ODF＝S△EBF，
∴阴影部分的面积＝S扇形DOE＝＝π．
故选：A．
【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了矩形的性质和扇形面积的计算．
7．（2022•南陵县自主招生）如图，AB和BC是⊙O的两条弦（即ABC是圆的一条折弦），BC＞AB，M是的中点，则从M向BC所作垂线的垂足D，若，，则CD的长为（ ）
A．B．C．D．
【分析】在CD上截取CE＝AB，连接CM，EM，BM，AM，证明△ABM≌△CEM，得出BM＝EM，进而得出BD＝DE即可解答．
【解答】解：如图，在CD上截取CE＝AB，连接CM，EM，BM，AM，
∵M是的中点，
∴AM＝CM，
又∠A＝∠C，
在△ABM和△CEM中，
，
∴△ABM≌△CEM（SAS），
∴BM＝EM，
∵MD⊥BC，
∴BD＝DE，
∵，，
∴CD＝CE+DE＝AB+BD＝2＝3．
故选：D．
【点评】本题考查了圆周角定理以及圆心角，弦，弧之间的关系定理，熟记定理并灵活运用是解题的关键，在同圆或等圆中，①圆心角相等，②所对的弧相等，③所对的弦相等，三项“知一推二”，一项相等，其余二项皆相等．这源于圆的旋转不变性．
二．填空题（共8小题）
8．（2022•长寿区自主招生）如图，工人师傅准备从一块斜边AB长为40cm的等腰直角△AOB材料上裁出一块以直角顶点O为圆心的面积最大的扇形，然后用这块扇形材料做成无底的圆锥（接缝处忽略），则圆锥的底面半径为 5 cm．
【分析】首先求得扇形的半径，然后利用弧长公式求得弧长，然后利用圆周长公式求得底面半径即可．
【解答】解：作OC⊥AB于点C，
∵△OAB是斜边长为40cm的等腰直角三角形，
∴OA＝OB＝20cm，
∴OC＝＝20cm，
∴扇形的弧长为＝10π，
设底面半径为r，则2πr＝10π，
解得：r＝5，
故答案为：5．
【点评】考查了圆锥的计算及扇形的面积的计算的知识，解题的关键是能够求得扇形的弧长，难度不大．
9．（2022•宁波自主招生）如图，在⊙O中、三条劣弧AB、BC、CD的长都相等，弦AC与BD相交于点E，弦BA与CD的延长线相交于点F，且∠F＝40°，则∠AED的度数为 70° ．
【分析】连接BC，根据弧相等，得到∠BAC＝∠BDC＝∠BCA＝∠DBC，设出∠ACD＝∠ABD＝x，根据外角的性质得出∠BAC＝x+40°，进而利用三角形的内角和求出x即可解答．
【解答】解：连接BC，
∵弧AB、BC、CD的长相等，
∴∠BAC＝∠BDC＝∠BCA＝∠DBC，
设∠ACD＝∠ABD＝x，
∵∠F＝40°，
∴∠BAC＝x+40°，
∴∠BDC＝∠BCA＝∠DBC＝x+40°，
在△ABC中，x+40°+x+x+x+40°+40°＝180°，
解得x＝15°，
∴∠DBC＝∠BCA＝55°，
∴∠AED＝∠BEC＝70°．
故答案为：70°．
【点评】本题考查了圆周角定理，解题的关键是熟记定理并灵活运用，圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
10．（2022•相城区校级自主招生）一直角三角形的斜边长为c，它的内切圆的半径是r，则内切圆的面积与三角形的面积的比是 ．
【分析】连接内心和直角三角形的各个顶点，设直角三角形的两条直角边是a，b．则直角三角形的面积是；又直角三角形内切圆的半径r＝，则a+b＝2r+c，所以直角三角形的面积是r（r+c）；因为内切圆的面积是πr2，则它们的比是．
【解答】解：设直角三角形的两条直角边是a，b，则有：
S＝，
又∵r＝，
∴a+b＝2r+c，
∴直角三角形的面积是r（r+c）．
又∵内切圆的面积是πr2，
∴它们的比是．
故答案是：．
【点评】此题要熟悉直角三角形的内切圆半径等于两条直角边的和与斜边的差的一半，能够把直角三角形的面积分割成三部分，用内切圆的半径进行表示，是解题的关键
11．（2022•北碚区自主招生）如图，在△ABC中，∠ACB＝90°，∠B＝60°，BC＝2，以AC为直径作半圆，交AB边于点D，点O为圆心，连接OD，则图中阴影部分的面积是 2﹣π ．
【分析】根据S阴影部分＝S△ABC﹣S扇形COD，进行计算即可．
【解答】解：∵∠ACB＝90°，∠B＝60°，BC＝2，
∴AC＝BC＝2，
∵OA＝OD，∠BAC＝90°﹣60°＝30°，
∴∠COD＝2∠BAC＝60°，
∴S阴影部分＝S△ABC﹣S扇形COD
＝××2﹣
＝2﹣π，
故答案为：2﹣π．
【点评】本题考查扇形面积的计算，掌握扇形面积的计算方法以及直角三角形的边角关系是正确解答的前提．
12．（2022•渝北区自主招生）如图，四边形BCDE内接于⊙O，AB是⊙O的直径，满足AB⊥CD于点F，连接AE，BD．若∠ABC＝∠DBE，CF＝2AF＝4，则点E到线段AB的距离为 ．
【分析】如图，连接OC，过点E作ER⊥AB于点R．设OA＝OC＝r．利用勾股定理求出r，再证明CD＝QE＝8，利用勾股定理求出BE，再利用面积法求出ER，可得结论．
【解答】解：如图，连接OC，过点E作ER⊥AB于点R．设OA＝OC＝r．
∵AB⊥CD，AB是直径，
∴CF＝DF＝4，＝，
在Rt△OCF中，r2＝42+（r﹣2）2，
∴r＝5，
∴AB＝10，
∵∠ABC＝∠DBE，
∴＝＝，
∴＝，
∴CD＝AE＝8，
∵AB是直径，
∴∠AEB＝90°，
∴BE＝＝＝6，
∵ER⊥AB，
∴S△ABE＝•AB•ER＝•AE•BE，
∴ER＝，
∴点E到线段AB的距离为．
故答案为：．
【点评】本题考查圆内接四边形的性质，垂径定理，勾股定理等知识，解题的关键是学会利用参数，构建方程解决问题，属于中考常考题型．
13．（2022•南岸区自主招生）如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，BC是半圆的直径，图中阴影部分的面积为4，则半圆的面积是 2π ．
【分析】根据扇形面积即三角形面积的计算方法进行解答即可．
【解答】解：如图，连接OD，DC，由对称性可知弓形①与弓形②的面积相等，
由阴影部分的面积为4，即S△BCD＝4，
设半径为x，则OB＝OC＝OD＝x，
所以BC•OD＝4，
即x2＝4，
所以半圆的面积为πx2＝π×4＝2π，
故答案为：2π．
【点评】本题考查扇形面积的计算，掌握等腰直角三角形的性质，扇形面积的计算方法是正确解答的前提．
14．（2022•鄞州区校级自主招生）如图，在⊙O的内接四边形ABCD中，AC⊥BD，CA＝CB，过点A作AC的垂线交CD的延长线于点E，连结BE．若cs∠ACB＝，则的值为 ．
【分析】设AC，BD交于点F，过点B作BG⊥EA，交EA的延长线于点G，利用直角三角形的边角关系得到cs∠ACB＝＝，设CF＝3k，则CB＝5k，利用勾股定理，相交弦定理，平行线分线段成比例定理求得BF，DF，AE，利用勾股定理求得线段CE；利用矩形的判定与性质和勾股定理求得BE，则结论可得．
【解答】解：设AC，BD交于点F，过点B作BG⊥EA，交EA的延长线于点G，如图，
∵AC⊥BD，cs∠ACB＝，
∴cs∠ACB＝＝，
设CF＝3k，则CB＝5k，
∴BF＝＝4k．
∵CA＝CB，
∴AC＝5k，
∴AF＝AC﹣CF＝2k．
∵CF•AF＝DF•BF，
∴DF＝k．
∵AC⊥BD，AE⊥AC，
∴DF∥AE，
∴，
∴，
∴AE＝k．
∴CE＝＝k．
∵AC⊥BD，AE⊥AC，BG⊥EA，
∴四边形AFBG为矩形，
∴BG＝AF＝2k，AG＝BF＝4k，
∴EG＝AE+AG＝k，
∴BE＝＝k，
∴＝，
故答案为：．
【点评】本题主要考查了矩形的性质，直角三角形的边角关系定理，勾股定理，相交弦定理，熟练掌握圆的相关性质，利用勾股定理求得对应相等的长度是解题的关键．
15．（2022•海曙区自主招生）如图，点A、B、C均在坐标轴上，AO＝BO＝CO＝1，过A、O、C作⊙D，E是⊙D上任意一点，连结CE，BE，则CE2+BE2的最大值是 6 ．
【分析】连接AC，OD，DE，设E（x，y），利用90°的圆周角所对的弦是直径可得，AC是⊙D的直径，再利用平面直角坐标系中的两点间距离公式求出CE2+BE2＝2（x2+y2）+2，OE2＝x2+y2，可得当OE为⊙D的直径时，OE最大，CE2+BE2的值最大，然后进行计算即可解答．
【解答】解：连接AC，OD，DE，
设E（x，y），
∵∠AOC＝90°，
∴AC是⊙D的直径，
∵AO＝BO＝CO＝1，
∴A（0，1），C（1，0），B（﹣1，0），
∴AC＝，
CE2＝（x﹣1）2+y2，
BE2＝（x+1）2+y2，
∴CE2+BE2＝（x﹣1）2+y2+（x+1）2+y2＝2（x2+y2）+2，
∵OE2＝x2+y2，
∴当OE为⊙D的直径时，OE最大，CE2+BE2的值最大，
∴OE2＝AC2＝（）2＝2，
∴CE2+BE2的最大值＝2×2+2＝6，
故答案为：6．
【点评】本题考查了三角形的外接圆与外心，勾股定理，圆周角定理，坐标与图形的性质，点与圆的位置关系，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
三．解答题（共3小题）
16．（2022•海曙区自主招生）如图，已知△ABC内接于⊙O，AB是该圆直径，D是弧AC上的点，线段BD与AC交于点E，若AB＝5，sin∠CAB＝＝k．
（1）试用含m的代数式表示k；
（2）若AD∥OC，求k的值．
【分析】（1）根据直径所对的圆周角是直角可得∠ACB＝90°，从而在Rt△ABC中，利用锐角三角函数的定义求出BC，再利用勾股定理求出AC，然后再证明△DEA∽△CEB，从而利用相似三角形的性质可得DE＝，
再结合已知可得BE2＝，最后在Rt△CEB中，利用勾股定理可得BE2＝m2+9，从而可得m2+9＝，进行计算即可解答；
（2）根据平行线的性质可得∠DAC＝∠ACO，根据等腰三角形的性质可得∠OAC＝∠ACO，再利用同弧所对的圆周角相等可得∠DAC＝∠DBC，从而可得∠DBC＝∠OAC，然后证明△CBE∽△CAB，从而利用相似三角形的性质可求出m的值，再代入（1）的结论进行计算即可解答．
【解答】解：（1）∵AB是⊙O的直径，
∴∠ACB＝90°，
∵AB＝5，sin∠CAB＝，
∴BC＝AB•sin∠CAB＝5×＝3，
∴AC＝＝＝4，
∵∠D＝∠ECB，∠DEA＝∠CEB，
∴△DEA∽△CEB，
∴＝，
∴＝，
∴DE＝，
∵＝k，
∴＝k，
∴BE2＝，
在Rt△CEB中，BE2＝CE2+BC2，
∴BE2＝m2+9，
∴m2+9＝，
∴k＝；
（2）∵AD∥OC，
∴∠DAC＝∠ACO，
∵OA＝OC，
∴∠OAC＝∠ACO，
∵∠DAC＝∠DBC，
∴∠DBC＝∠OAC，
∵∠ACB＝∠BCE，
∴△CBE∽△CAB，
∴＝，
∴＝，
∴m＝，
∴k＝＝＝，
∴k的值为．
【点评】本题考查了三角形的外接圆与外心，圆周角定理，锐角三角函数的定义，相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．
17．（2022•南陵县自主招生）如图，已知圆O，弦AB、CD相交于点M．
（1）求证：AM•MB＝CM•MD；
（2）若M为CD中点，且圆O的半径为3，OM＝2，求AM•MB的值．
【分析】（1）利用同弧所对的圆周角相等，证明△ADM∽△CBM；
（2）连接OM、OC，由于M是CD的中点，由垂径定理得OM⊥CD，利用勾股定理可求出CM的值，根据（1）的结论，求出AM•BM．
【解答】解：（1）∵∠A＝∠C，∠D＝∠B，
∴△ADM∽△CBM
∴，
即AM•MB＝CM•MD．
（2）连接OM、OC．
∵M为CD中点，
∴OM⊥CD
在Rt△OMC中，
∵OC＝3，OM＝2
∴CM＝DM＝，
由（1）知AM•MB＝CM•MD．
∴AM•MB＝•＝5．
【点评】本题考查了相似三角形的判定和性质、勾股定理、圆周角定理及垂径定理，是综合性较强的题目．（1）利用相似、圆周角定理得到相交弦定理；（2）中利用垂径定理、勾股定理和相交弦定理得到了AM与BM的积．相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．
18．（2022•宁波自主招生）如图，在Rt△ABC中，AC＝3，BC＝4，CD是斜边AB上的高，I1、I2，分别是△ACD、△BCD的内心，直线I1I2，分别交AC、BC于点E、F．
（1）求tan∠I1I2D；
（2）求△CEF的面积．
【分析】（1）由题意易得：I1D⊥I2D，AB＝5，过点I1作I1G⊥AB于点G，所以I1G是直角三角形ADC内切圆半径，I1G＝（AD+CD﹣AC）＝，再利用三角函数分别计算出I1D、I2D，即可解答；
（2）证明CE＝CF＝CD，即可解答．
【解答】解：（1）如图：连接AI1、CI1、CI2，
∵三角形内心是三条角平分线的交点，且I1、I2分别是△ACD，△BCD的内心，
∴∠1＝∠2，∠3＝∠4，
又∵∠1+∠2＝90°，∠3+∠4＝90°，
∴2∠2+2∠3＝90°+90°＝180°，
∴∠2+∠3＝90°，即∠I1DI2＝90°，
∴I1D⊥I2D，
在直角三角形ABC中，AC＝3，BC＝4，
∴AB＝＝5，
又∵CD⊥AB，
∴AD＝＝，
∴BD＝AB﹣AD＝，CD＝＝，
过点I1作I1G⊥AB于点G，
则I1G是直角三角形ADC内切圆半径，
∴I1G＝（AD+CD﹣AC）＝，
则DI1＝＝＝，DG＝，
同理：DI2＝，
则tan∠I1I2D＝＝×＝；
（2）由（1）可知：＝＝，
∴＝，
∵∠I1DI2＝∠ACB＝90°，
∴△I1DI2∽△ACB，
∴∠I1I2D＝∠B＝∠ACD，
∴∠CEF＝∠CDI2＝45°，
∵CI1＝CI1，∠ECI2＝∠DCI2，
∴△ECI1≌△DCI1（AAS），
∴CE＝CD＝，
∴CF＝CE＝，
故三角形CEF面积为．
【点评】本题考查三角形内切圆的性质、三角形的面积计算、三角函数、勾股定理等知识点，解题关键是熟练掌握以上性质．