2024年湖南省常德市中考一模数学试题（原卷版+解析版）

这是一份2024年湖南省常德市中考一模数学试题（原卷版+解析版），文件包含2024年湖南省常德市中考一模数学试题原卷版docx、2024年湖南省常德市中考一模数学试题解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

2．必须在答题卡上答题，在草稿纸、试题卷上答题无效；
3．答题时，请考生注意各大题题号后面的答题提示；
4．请勿折叠答题卡，保持字体工整、笔迹清晰、卡面清洁；
5．答题卡上不得使用涂改液、涂改胶和贴纸；
6．本学科试卷共26道题目，考试时量120分钟，满分120分．
一、选择题（在下列各题的四个选项中，只有一项是符合题意的，请在答题卡中填涂符合题意的选项．本大题共10个小题，每小题3分，共30分）
1. 下列各数中，是无理数的是（ ）
A. B. C. D. 2024
【答案】B
【解析】
【分析】本题考查了无理数的定义，掌握无理数的常见形式“①最终结果含有开方开不尽的数，②最终结果含有的数，③形如（每两个增加一个）．”是解题的关键．
【详解】解：A.是有理数，故不符合题意；
B.是无理数，故符合题意；
C.是有理数，故不符合题意；
D. 2024是有理数，故不符合题意；
故选：B．
2. 下列图形中，是中心对称图形的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查中心对称图形的识别，根据定义“如果一个图形绕一点旋转180度后能与自身重合，这个图形叫做中心对称图形”逐项判断即可．
【详解】解：根据中心对称图形的定义可知：
A，不是中心对称图形，不合题意；
B，不是中心对称图形，不合题意；
C，是中心对称图形，符合题意；.
D，不是中心对称图形，不合题意；
故选C．
3. 下列计算正确的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】此题考查了同底数幂的除法，幂的乘方，完全平方公式，单项式乘以多项式；熟练掌握公式，，及法则是解本题的关键．
【详解】解：A.，结论正确，故符合题意；
B.，结论错误，故不符合题意；
C.，结论错误，故不符合题意；
D.，结论错误，故不符合题意；
故选：A．
4. 长沙市2023年1月至9月地区生产总值约10674亿元，同比增长．其中数据10674亿用科学记数法表示为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题主要考查了科学记数法．熟练掌握科学记数法的定义是解决问题的关键．科学记数法的定义：把一个绝对值大于10的数表示成 (其中，n是正整数)，使用的是科学记数法．
根据科学记数法的表现形式解答，这里，．
【详解】
故选：A
5. 已知三角形的两边长分别为5，8，另一边长可能是（ ）
A. B. 14C. 2D. 5
【答案】D
【解析】
【分析】本题考查了三角形的三边关系，设另一边长为，由三角形的三边关系得，即可求解；理解三角形的三边关系：“任意两边之和大于第三条边，任意两边之差小于第三边．”是解题的关键．
【详解】解：设另一边长为，则有
，
，
故选：D．
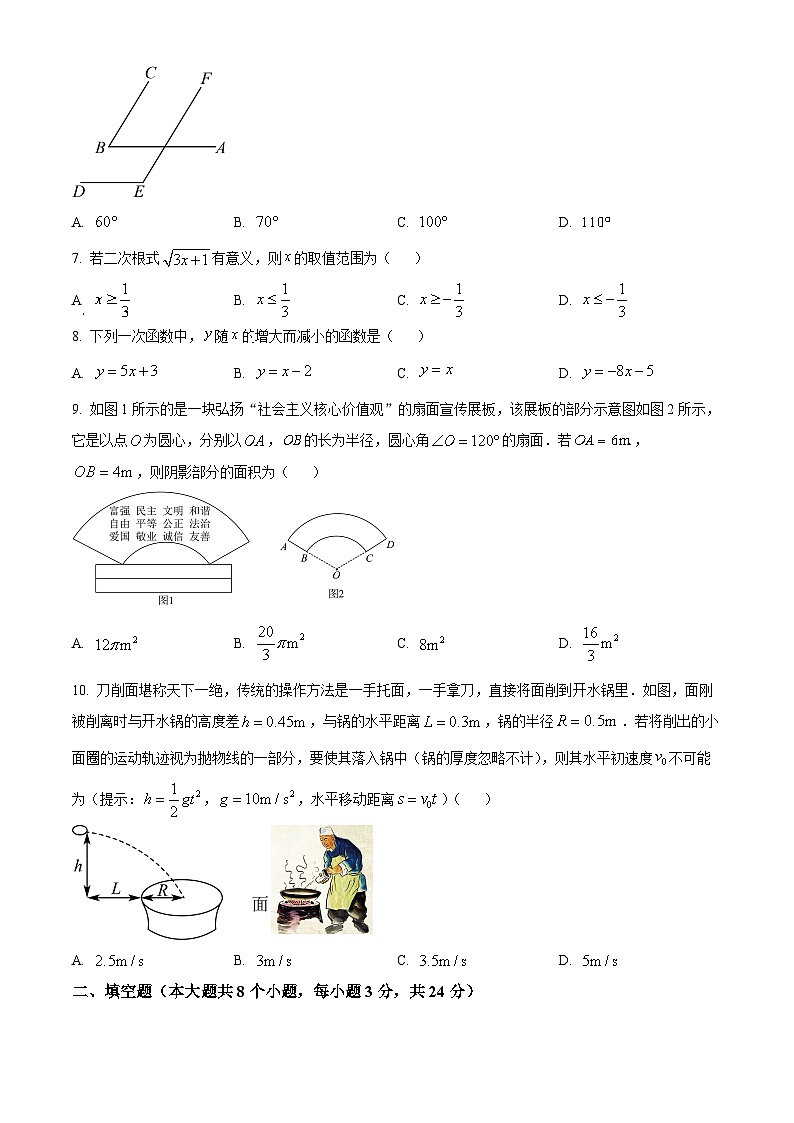
6. 如图，，，若，则的度数为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查平行线的性质，根据两直线平行，同旁内角互补求得，再两直线平行，内错角相等可得．熟练掌握平行线的性质是解题的关键．
【详解】解：如图，
∵，，
∴，
∵，
∴，
∴的度数为．
故选：B．
7. 若二次根式有意义，则的取值范围为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查二次根式有意义的条件，解题的关键是掌握二次根式中的被开方数是非负数．据此列出不等式求解即可．
【详解】解：∵二次根式有意义，
∴，
解得：．
故选：C．
8. 下列一次函数中，随的增大而减小的函数是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了一次函数的性质，理解一次函数的性质“当时，随的增大而增大；当时，随的增大而减小．”是解题的关键．
【详解】解：A.，，随的增大而增大，故不符合题意；
B.，，随的增大而增大，故不符合题意；
C.，，随的增大而增大，故不符合题意；
D.，，随的增大而减小，故符合题意；
故选：D．
9. 如图1所示的是一块弘扬“社会主义核心价值观”的扇面宣传展板，该展板的部分示意图如图2所示，它是以点为圆心，分别以，的长为半径，圆心角的扇面．若，，则阴影部分的面积为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查扇形面积的计算，根据，计算即可．掌握扇形的面积公式是解题的关键．
【详解】解：∵如图是以点为圆心，分别以，的长为半径，圆心角的扇面，且，，
∴
，
∴阴影部分的面积为．
故选：B．
10. 刀削面堪称天下一绝，传统的操作方法是一手托面，一手拿刀，直接将面削到开水锅里．如图，面刚被削离时与开水锅的高度差，与锅的水平距离，锅的半径．若将削出的小面圈的运动轨迹视为抛物线的一部分，要使其落入锅中（锅的厚度忽略不计），则其水平初速度不可能为（提示：，，水平移动距离）（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了二次函数的应用，要使其落入锅中，需要满足，由即可求解；找出的取值范围是解题的关键．
【详解】解：由题意得
，
解得：，（舍去），
要使其落入锅中，
，
，
，
，
，
不可能；
故选：D．
二、填空题（本大题共8个小题，每小题3分，共24分）
11. 分解因式：______．
【答案】
【解析】
【分析】本题考查提公因式法与公式法分解因式，掌握因式分解的方法是解决问题的关键．
【详解】解：，
故答案为：．
12. 睡眠管理作为“五项管理”中重要的内容之一，也是学校教育重点关注的内容．某老师了解到班上某位学生的7天睡眠时间（单位：小时）如下：10，9，9，8，8，10，9，则该学生这7天的平均睡眠时间是_____小时．
【答案】
【解析】
【分析】本题考查了算术平均数的定义，掌握算术平均数的求法：是解题的关键．
【详解】解：由题意得
（小时），
故答案：．
13. 关于的一元二次方程有实数根，则的取值范围为______．
【答案】且
【解析】
【分析】本题考查了由一元二次方程根的判别式求参数的值；，由一元二次方程有实数根，可得即可求解；掌握根的判别式“时，方程有两个不相等的实数根；时，方程有两个相等的实数根；时，方程有无的实数根．”是解题的关键．
【详解】解：由题意得
，
一元二次方程有实数根，
，，
即：
解得：，
且．
14. 如图，已知，以点为圆心，以适当长度为半径画弧，分别交，于点，，再分别以点，为圆心，大于的长为半径画弧，两弧交于点，作射线，过点作交于点，则的度数是______度．
【答案】
【解析】
【分析】本题考查了角平分线的作法，平行线的性质；角平分线的作法得平分，再由平行线的性质，即可求解；理解角平分线的作法是解题的关键．
【详解】解：由作法得：
平分，
，
，
，
故答案：．
15. 已知，为一元二次方程的两实根，则______．
【答案】
【解析】
【分析】本题考查了求一元二次方程的根与系数的关系；由根与系数的关系得，将此代入化简后的分式，即可求解；掌握根与系数的关系： 是解题的关键．
【详解】解：，
，为一元二次方程两实根，
，
原式；
故答案：．
16. 如图，在平面直角坐标系中，点在反比例函数（为常数，，）的图像上，过点作轴的垂线，垂足为，连接．若的面积为，则______．
【答案】
【解析】
【分析】本题考查反比例函数的图像，反比例函数比例系数的几何意义，根据点在反比例函数的图像上，轴于，由反比例函数比例系数的几何意义得，然后根据的面积为可得出的值．熟练掌握反比例函数比例系数的几何意义是解题的关键．
【详解】解：∵点在反比例函数的图像上，轴于，
∴，
∴，
∵的面积为，
∴，
∵，
∴．
故答案为：．
17. 如图，点，，在半径为的上，，，垂足为，交于点，连接，已知，则______．
【答案】
【解析】
【分析】本题考查了圆的基本性质，等腰三角形的性质，直角三角形的特征；由圆周角定理得，由等腰三角形的性质得，由直角三角形的特征即可求解；掌握性质是解题的关键．
【详解】解：如图，连接，
，
，
，
，
，
，
，
；
故答案：．
18. 如图，已知点是第一象限内的一个定点，若点是以点为圆心，4为半径的圆上的一个动点，连接，过点作，且．当点在上运动一周时，点运动的路径长是______．
【答案】
【解析】
【分析】本题考查隐圆问题、相似三角形的判定和性质，连接，过点作，且，构造，推出，可得以点C为圆心，长为半径的圆即为点运动的轨迹，求的周长即可．求出点B的运动轨迹是解题的关键．
【详解】解：如图，连接，过点作，且，连接，，以点C为圆心，长为半径作圆，
，，
，
，即，
又，，
，
，
，
，
以点C为圆心，长为半径的圆即为点运动的轨迹，
点运动的路径长为：，
故答案为：．
三、解答题（本大题共8个小题，第19、20题每小题6分，第21、22题每小题8分，第23、24题每小题9分，第25、26题每小题10分，共66分．解答应写出必要的文字说明、证明过程或演算步骤）
19. 先化简，再求值：，其中．
【答案】，
【解析】
【分析】本题考查分式的化简求值，先利用异分母分式加减法法则计算括号里，再算括号外的除法，然后把的值代入化简后的式子进行计算，即可解答．
【详解】解：
，
当时，
原式．
20. 2023年5月30日9点31分，“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射，成功把景海鹏、桂海潮、朱杨柱三名航天员送入中国空间站．如图，在发射的过程中，飞船从地面处发射，当飞船到达处时，从位于地面处的雷达站测得仰角为；后飞船到达处，此时从处测得仰角为．已知飞船从处到处的平均速度为，求雷达站到飞船发射点的距离．（结果精确到，）
【答案】
【解析】
【分析】本题考查了解直角三角形的应用，由等腰三角形的性质得，设，由正切的定义得，求出，即可求解；找出对应的仰角，掌握解直角三角形的方法是解题的关键．
【详解】解：由题意得
，
（）
（），
，
，
，
设，
在中，
，
，
，
解得：；
故雷达站到飞船发射点的距离．
21. 2023年11月7日，世界互联网大会“互联网之光”博览会在浙江乌镇开幕，大会主题为“建设包容、普惠、有韧性数字世界——携手构建网络空间命运共同体”．为增强学生网络常识及安全意识，某校举行了一次全校6000名学生参加的安全知识竞赛．从中随机抽取名学生的竞赛成绩进行了分析，把成绩（满分100分，所有竞赛成绩均不低于60分）分成四个等级（：；：；：；：），并根据分析结果绘制了不完整的频数分布直方图和扇形统计图．
请根据以上信息，解答下列问题：
（1）填空：______，______；
（2）请补全频数分布直方图；
（3）扇形统计图中等级所在扇形的圆心角度数为______；
（4）若把等级定为“优秀”等级，请你估计该校参加竞赛的6000名学生中达到“优秀”等级的学生人数．
【答案】（1），
（2）见详解 （3）
（4）估计人
【解析】
【分析】本题考查了从关联统计图中获取信息，样本估计总体；
（1）由等级人数除以所占百分比，即可求出抽取的总人数，从而可求出，即可求解；
（2）可求等级的人数为，补全图，即可求解；
（3）所占百分比，即可求解；
（4）用样本中等级人数除以所占百分比乘以总人数，即可求解；
能正确从频数分布直方图和扇形统计图中获取信息是解题的关键．
【小问1详解】
解：由频数分布直方图和扇形统计图得
等级有人占，
，
，
；
故答案：，；
【小问2详解】
解：由题意得
等级的人数为：
（人）；
补全图，如下：
【小问3详解】
解：由题意得
，
故答案：；
【小问4详解】
解：由题意得
（人），
答：估计该校参加竞赛的6000名学生中达到“优秀”等级的学生人数为人．
22. 如图，是的直径，点和点是上的两点，延长到点，连接，，，且．

（1）求证：为的切线；
（2）若，求阴影部分的面积．
【答案】（1）见详解 （2）
【解析】
【分析】本题考查了切线的判定，求扇形中不规则图形的阴影部分面积；
（1）连接，由圆的基本性质得，结合等腰三角形的性质得，由直径所对的圆周角是直角得，即可求解；
（2）由勾股定理得，由即可求解；
掌握切线的判定方法“连半径，证垂直”，能将不规则图形的面积转化为规则图形面积的和差是解题的关键．
【小问1详解】
证明：如图，连接，

，
，
，
，
，
，
，
是直径，
，
，
，
，
，
为的切线；
【小问2详解】
解：，
，
，
，
，，
，
是等边三角形，
，
；
23. 党的二十大报告提出：“加快建设高质量教育体系，发展素质教育”．某校为响应二十大报告的育人精神，进一步落实“德、智、体、美、劳”五育并举工作，有效开展“阳光体育”活动，该校计划从体育用品商场购买乒乓球拍和羽毛球拍用于“阳光体育大课间”和学生社团活动．已知一副羽毛球拍比一副乒乓球拍多元，且用元购买乒乓球拍的数量和用元购买羽毛球拍的数量一样．
（1）求每副乒乓球拍和每副羽毛球拍的价格；
（2）学校计划采购乒乓球拍和羽毛球拍共计副，且乒乓球拍的数量不超过羽毛球拍数量的倍，求最多购买乒乓球拍多少副．
【答案】（1）每副乒乓球拍的价格是元，每副羽毛球拍的价格是元
（2）最多购买乒乓球拍副
【解析】
【分析】本题考查分式方程的应用以及一元一次不等式的应用，
（1）设每副乒乓球拍的价格是元，则每副羽毛球拍的价格是元，利用数量总价单价，根据“用元购买乒乓球拍的数量和用元购买羽毛球拍的数量一样”可列出关于的分式方程，解之经检验后，可得出每副乒乓球拍的价格，再将其代入中，即可求出每副羽毛球拍的价格；
（2）设购买乒乓球拍副，则购买羽毛球拍副，根据“乒乓球拍的数量不超过羽毛球拍数量的倍”可列出关于的一元一次不等式，解之可得出的取值范围，再取其中的最大整数值即可；
解题的关键是：（1）找准等量关系，正确列出分式方程；（2）根据各数量之间的关系，正确列出一元一次不等式．
【小问1详解】
解：设每副乒乓球拍价格是元，则每副羽毛球拍的价格是元，
根据题意得：，
解得：，
经检验，是所列方程的解且符合题意，
∴（元）．
答：每副乒乓球拍的价格是元，每副羽毛球拍的价格是元；
【小问2详解】
设购买乒乓球拍副，则购买羽毛球拍副，
根据题意得：，
解得：，
又∵为正整数，
∴的最大值为．
答：最多购买乒乓球拍副．
24. 如图，四边形是正方形，点为边上一点，连接并延长，交的延长线于点，连接交于点，连接．
（1）求证：；
（2）求证：；
（3）已知，求．
【答案】（1）见详解 （2）见详解
（3）
【解析】
【分析】本题考查了正方形的性质，全等三角形的判定及性质，三角形相似的判定及性质；
（1）由正方形的性质得，，由即可得证；
（2）由平行线的性质得，由全等三角形的性质得，即可得证；
（3）由得，由三角形相似的性质得，设，则有，由相似三角形的性质得，即可求解；
掌握判定方法及性质，能用辅助未知数进行求解是解题的关键．
【小问1详解】
证明：四边形是正方形，
，
，
在和中
，
（）；
【小问2详解】
证明：四边形正方形，
，
，
由（1）得：，
，
，
，
；
【小问3详解】
证明：四边形是正方形，
，
，
，
设，则有，
，
，
，
，
，
；
故．
25. 如图，为的直径，点为半径上异于点和点的一个点，过点作与直径垂直的弦，连接，作，连接，，交于点，且与相切于点．
（1）求证：；
（2）若的半径为5，，求的长；
（3）已知，，求与之间的函数关系．
【答案】（1）见详解 （2）
（3）
【解析】
【分析】（1）连接，由切线的性质得，由可判定，由全等三角形的性质得，由圆的基本性质得，即可的证；
（2）由正切函数的定义及垂径定理得，，设，则，由勾股定理得，即可求解；
（3）由可判定，由相似三角形的性质得，由相似三角形的判定方法得，由相似三角形的性质得，即可求解．
【小问1详解】
证明：如图，连接，
，，
与相切于点，
，
，
，
在和中
，
（），
，
，
，
；
【小问2详解】
解：，，
，，
设，则，
，
在中，，
，
整理得：，
解得：，（舍去），
，
；
【小问3详解】
解：，，
，
，
，
，
，
，
，
，
，
，
，
，
．
【点睛】本题考查了圆的基本性质，垂径定理，切线的性质，全等三角形的判定及性质，相似三角形的判定及性质，勾股定理等；掌握判定方法及性质，能熟练利用勾股定理解“弦的一半，弦心距、半径”构成的直角三角形以及比例线段之间的相互转换是解题的关键．
26. 中央广播电视总台《2024年春节联欢晚会》以“龙行龘龘，欣欣家国”为主题，引领全球华人迈向生机盎然、充满希望的甲辰龙年．若抛物线与轴交于，两点，与轴交于点，且恰好是直角三角形，并满足（为坐标原点），则称抛物线是“龘龘欣欣抛物线”，其中较短直角边所在直线为“龘龘线”，较长直角边所在直线为“欣欣线”．
（1）若“龘龘欣欣抛物线”的“龘龘线”为直线，求抛物线解析式；
（2）已知“龘龘欣欣拋物线”与轴的一个交点为，其“欣欣线”与反比例函数的图象仅有一个交点，求反比例函数解析式；
（3）已知“龘龘欣欣抛物线”的“龘龘线”“欣欣线”及轴围成的三角形面积的取值范围是，令，且有最大值，求的值．
【答案】（1）
（2）
（3）
【解析】
【分析】（1）求出直线与坐标轴的交点，根据，求出点坐标，待定系数法求出函数解析式即可；
（2）将点代入解析式，得到，根据对称性求出抛物线与轴的另一个交点的坐标为，结合，求出的值，进而求出“欣欣线”的解析式，联立直线和反比例函数的解析式，根据只有一个交点，得到，进而求出的值，即可得出结论；
（3）根据根据与系数的关系，结合，求出的值，进而求出的值，再根据三角形的面积为，以及的取值范围求出的取值范围，再根据，结合二次函数的性质，分三种情况进行讨论求解即可．
【小问1详解】
解：∵，
∴当时，，当时，，
∴不妨设，，
∴，，
∵，
∴，
∴或
∵为直角三角形，
∴，
∵抛物线经过三点，
∴设抛物线的解析式为：，将代入，得：
，
解得：，
∴；
【小问2详解】
∵与轴的一个交点为，
∴，对称轴为直线，
∴，抛物线与轴的另一个交点为，
当时，，
∴，
∵，
∴，
∴，
解得：（不合题意，舍去）或或，
∴或，
∴抛物线与坐标轴的交点坐标为或，
∵为直角三角形，
∴交点坐标为；
设，
则，
∴“欣欣线”为所在直线，
设直线的解析式为，把代入，得：，解得：，
∴，
令，整理得：，
∵直线和双曲线只有一个交点，
∴，
∴，
∴反比例函数的解析式为；
【小问3详解】
∵，
∴当时，，
∴，
设抛物线与轴的两个交点坐标为，
则：，
∴，
∵，
∴，解得：（舍去）或或，
∵抛物线的开口向上，当时，抛物线与轴的两个交点均在轴的正半轴，不是直角三角形，
∴，
∴，
令，则：，
∴，
∴，
∴，
∵，
∴，
∴，
∴，
∵，
∴
∵，
当时，则当时，有最大值为：，解得：；
当时，则：当时，有最大值为：，解得：或（均舍去）；
当时，则：当时，有最大值为：，解得：（不满足题意，舍去）；
综上：．
【点睛】本题考查二次函数的综合应用，涉及到二次函数与坐标轴的交点问题，一次函数与坐标轴的交点问题，一次函数与反比例函数的交点问题，二次函数的最值问题，综合性强，难度大，计算量大，属于压轴题，读懂题意，理解“龘龘线”“欣欣线”的定义，是解题的关键．