所属成套资源:【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用)
- 专题1.3 原函数与导函数混合还原问题-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用) 试卷 1 次下载
- 专题1.4 切线与公切线-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用) 试卷 1 次下载
- 专题1.6 比大小(构造函数,切线放缩与泰勒展开)-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用) 试卷 1 次下载
- 专题1.7 嵌套(复合)函数问题综合-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用) 试卷 1 次下载
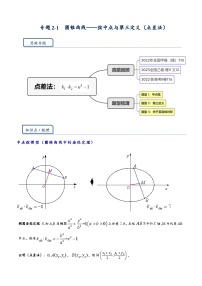
- 专题2.1 弦中点与第三定义(点差法)-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用) 试卷 1 次下载
专题1.5 抽象函数赋值与构造-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用)
展开
这是一份专题1.5 抽象函数赋值与构造-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用),文件包含专题1-5抽象函数赋值与构造原卷版docx、专题1-5抽象函数赋值与构造解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
一、抽象函数的赋值法
赋值法是求解抽象函数问题最基本的方法,复制规律一般有以下几种:
1、……-2,-1,0,1,2……等特殊值代入求解;
2、通过的变换判定单调性;
3、令式子中出现及判定抽象函数的奇偶性;
4、换为确定周期性.
二、判断抽象函数单调性的方法:
(1)凑:凑定义或凑已知,利用定义或已知条件得出结论;
(2)赋值:给变量赋值要根据条件与结论的关系.有时可能要进行多次尝试.
= 1 \* GB3 ①若给出的是“和型”抽象函数,判断符号时要变形为:
或;
= 2 \* GB3 ②若给出的是“积型”抽象函数,判断符号时要变形为:
或.
三、常见的抽象函数模型
1、可看做的抽象表达式;
2、可看做的抽象表达式(且);
3、可看做的抽象表达式(且);
4、可看做的抽象表达式.
2022新高考2卷T8
1.已知函数的定义域为R,且,则( )
A.B.C.0D.1
2023新高考1卷T11
2.(多选)已知函数的定义域为,,则( ).
A.B.
C.是偶函数D.为的极小值点
重点题型·归类精讲
2023·山东青岛·统考三模
设为定义在整数集上的函数,,,,对任意的整数均有.则______.
2023·山东滨州·三模
(多选)已知连续函数对任意实数x恒有,当时,,,则以下说法中正确的是( )
A.f(0)=0
B.f(x)是R上的奇函数
C.f(x)在[-3,3]上的最大值是6
D.不等式的解集为
安徽省皖江名校联盟2024届高三上学期10月第二次联考
已知函数不是常数函数,且满足以下条件:①,其中;②,则( )
A.0B.1C.2D.
(多选)已知定义在上的函数满足,且,则( )
A.B.
C.D.
已知函数及其导函数的定义域均为,对任意的,恒有,则下列说法正确的个数是( )
①;②必为奇函数;③;④若,则.
A.1B.2C.3D.4
2023·浙江嘉兴·统考模拟
已知函数的定义域为,且,,则的值是( )
A.9B.10C.11D.12
2023届江苏连云港校考
已知函数,任意,满足,且,则的值为( )
A.B.0C.2D.4
已知,都是定义在上的函数,对任意x,y满足,且,则下列说法正确的是( )
A.B.函数的图象关于点对称
C.D.若,则
2023绍兴·高二期末
已知函数的定义域为R,且,为奇函数,,则( )
A.B.C.0D.
(多选)已知函数的定义域为,,则( )
A.B.是奇函数
C.为的极小值点D.若,则
(多选)设是定义在上的函数,对,有,且,则( )
A.
B.
C.
D.
(多选)已知函数及其导函数的定义域均为,对任意的,恒有,则下列说法正确的有( )
A.B.必为奇函数
C.D.若,则
已知函数的定义域为,满足,且,则( )
A.B.为奇函数
C.D.
(多选)已知定义域为的函数对任意实数都有,且,则以下结论一定正确的有( )
A.B.是偶函数
C.关于中心对称D.
函数的定义域为,且,,,则 .
已知函数满足:,则 .
已知函数定义域为,满足,则 .
设为定义在整数集上的函数,,,,对任意的整数均有.则 .
(2024届厦门一中校考)若定义域为的奇函数满足,且,则 .
函数的定义域为,对任意,恒有,若,则 , .
深圳市宝安区2024届高三上学期10月调研数学试题
已知函数的定义域为,且,,为偶函数,则( )
A.为偶函数B.
C.D.
相关试卷
这是一份专题1.4 切线与公切线-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用),文件包含专题1-4切线与公切线原卷版docx、专题1-4切线与公切线解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
这是一份专题1.3 原函数与导函数混合还原问题-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用),文件包含专题1-3原函数与导函数混合还原问题原卷版docx、专题1-3原函数与导函数混合还原问题解析版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
这是一份专题1.2 指对同构(朗博同构)-【模型技巧】备考2024高考数学二轮复习重难点突破专题(新高考专用),文件包含专题1-2指对同构朗博同构原卷版docx、专题1-2指对同构朗博同构解析版docx等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。