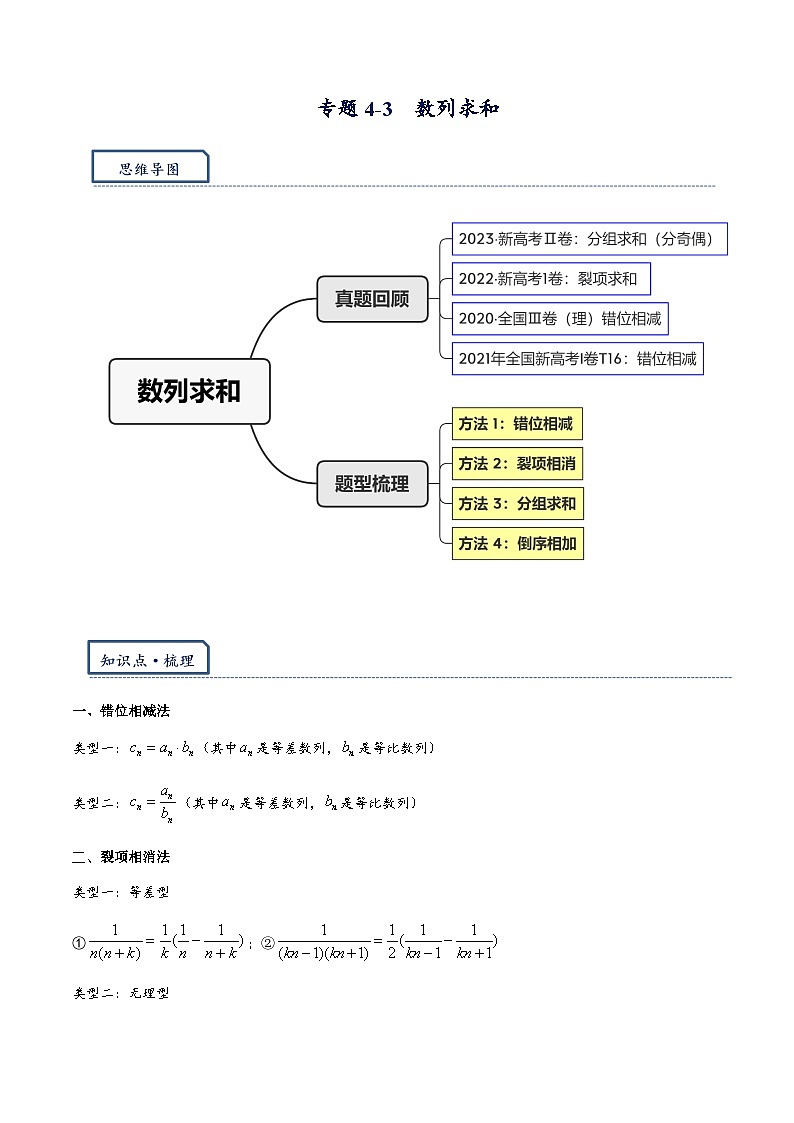
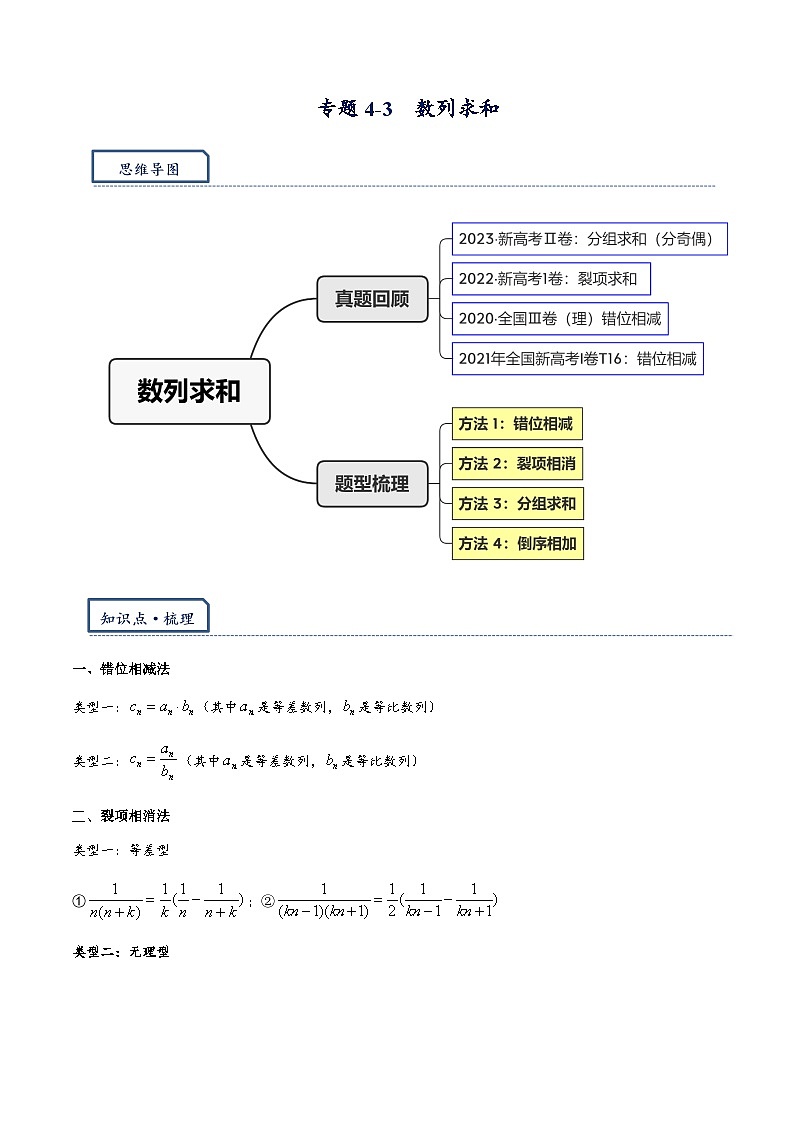
专题4.3 数列求和：错位，裂项，分组，倒序-【模型技巧】备考2024高考数学二轮复习重难点突破专题（新高考专用）

这是一份专题4.3 数列求和：错位，裂项，分组，倒序-【模型技巧】备考2024高考数学二轮复习重难点突破专题（新高考专用），文件包含专题4-3数列求和错位裂项分组倒序原卷版docx、专题4-3数列求和错位裂项分组倒序解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

一、错位相减法
类型一：（其中是等差数列，是等比数列）
类型二：（其中是等差数列，是等比数列）
二、裂项相消法
类型一：等差型
= 1 \* GB3 ①；②
类型二：无理型
类型三：指数型
类型四：通项裂项为“”型
，本类模型典型标志在通项中含有乘以一个分式.
类型五：分母为指数型乘2个一次函数型
三、分组求和法
2.1如果一个数列可写成的形式，而数列，是等差数列或等比数列或可转化为能够求和的数列，那么可用分组求和法.
2.2如果一个数列可写成的形式，在求和时可以使用分组求和法.
四、倒序相加法
即如果一个数列的前项中，距首末两项“等距离”的两项之和都相等，则可使用倒序相加法求数列的前项和
2023·新高考Ⅱ卷——分奇偶（分组）求和
1. 已知为等差数列，，记，分别为数列，的前n项和，，．
(1)求的通项公式；
(2)证明：当时，．
【答案】(1)；(2)证明见解析.
【分析】（1）设等差数列的公差为，用表示及，即可求解作答.
（2）方法1，利用（1）的结论求出，，再分奇偶结合分组求和法求出，并与作差比较作答；方法2，利用（1）的结论求出，，再分奇偶借助等差数列前n项和公式求出，并与作差比较作答.
【详解】（1）设等差数列的公差为，而，
则，
于是，解得，，
所以数列的通项公式是.
（2）方法1：由（1）知，，，
当为偶数时，，
，
当时，，因此，
当为奇数时，，
当时，，因此，
所以当时，.
方法2：由（1）知，，，
当为偶数时，，
当时，，因此，
当为奇数时，若，则
，显然满足上式，因此当为奇数时，，
当时，，因此，
所以当时，.
2022·新高考1卷——裂项求和
2. 已知，证明：．
【详解】
∴
2020·全国Ⅲ卷（理）——错位相减
3. 已知，求数列的前n项和Sn.
方法一：（通性通法）根据通项公式的特征，由错位相减法求解即可．
（2）由（1）可知，
［方法一］：错位相减法
，①
，②
由①②得：
，
即.
［方法二］【最优解】：裂项相消法
，所以．
［方法三］：构造法
当时，，设，即，则，解得．
所以，即为常数列，而，所以．
故．
［方法四］：
因为，令，则
，
，
所以．
故．
【点评】方法一：根据通项公式的特征可知，可利用错位相减法解出，该法也是此类题型的通性通法；
方法二：根据通项公式裂项，由裂项相消法求出，过程简单，是本题的最优解法；
方法三：由时，，构造得到数列为常数列，从而求出；
方法四：将通项公式分解成，利用分组求和法分别求出数列的前项和即可，其中数列的前项和借助于函数的导数，通过赋值的方式求出，思路新颖独特，很好的简化了运算．
2021年全国新高考I卷T16
4. 某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折，规格为的长方形纸，对折1次共可以得到，两种规格的图形，它们的面积之和，对折2次共可以得到，，三种规格的图形，它们的面积之和，以此类推，则对折4次共可以得到不同规格图形的种数为 ；如果对折次，那么 .
【答案】 5
【详解】（1）由对折2次共可以得到，，三种规格的图形，所以对着三次的结果有：，共4种不同规格（单位；
故对折4次可得到如下规格：，，，，，共5种不同规格；
（2）由于每次对着后的图形的面积都减小为原来的一半，故各次对着后的图形，不论规格如何，其面积成公比为的等比数列，首项为120,第n次对折后的图形面积为，对于第n此对折后的图形的规格形状种数，根据（1）的过程和结论，猜想为种（证明从略），故得猜想，
设，
则，
两式作差得：
，
因此，.
重点题型·归类精讲
题型一 错位相减
已知，若数列满足，求和：．
【答案】
【详解】因为，
所以，
两式相减得
又满足上式，所以
又，所以
则
，
，
两式相减得：
.
已知正项数列的前n项和为，且满足，
(1)求(2)求
【答案】(1)；(2)
【分析】(1)先令求出首项，再由数列的递推公式，当时，代入并结合
等差数列的定义和通项公式求出.
【详解】（1）根据题意可得，当时，，解得，
由，代入得，整理后得
，即，根据等差数列的定义可知，数列
是首项为1，公差为1的等差数列，则，
（2）由(1)可知，
，
（2023秋·江苏·高三校联考阶段练习）已知数列满足，且．
(1)求的通项公式；
(2)若数列的前项和为，且，求数列的前项和．
【答案】(1)；(2)
【分析】（1）由已知可得，然后利用累加法求出，从而可求得的通项公式；
（2）由结合（1）可求出，然后利用错位相减法可求得结果.
【详解】（1）因为，所以，
所以
，
所以．
（2）因为，所以当时，，得；
当时，，所以（时也成立）．
因为，所以，
所以
，故．
记数列的前n项和为，且．
(1)求数列的通项公式；
(2)设m为整数，且对任意，，求m的最小值．
【答案】(1);(2)7
【分析】（1）由数列与的关系可得，再结合等比数列的通项可得解；
（2）利用错位相减法求出，结合范围即可得解.
【详解】（1）因为，所以，
当时，，故，
且不满足上式，
故数列的通项公式为
（2）设，则，
当时，，
故，
于是．
整理可得，所以，
又，所以符合题设条件的m的最小值为7
（2023·江苏徐州·校考模拟预测）已知，集合，将集合的所有非空子集中最小的元素相加，其和记为，求．
【答案】
【详解】，集合的非空子集有个，
其中最小元素为1的集合中，含1个元素的集合有1个，含2个元素的集合有个，
含3个元素的集合有个，……，含个元素的集合有个，
所以最小元素为1的子集个数为个，
同理，最小元素为2的子集个数为个，
……，最小元素为的子集个数为1个，
∴，
，
∴，则．
已知设，求数列的前n项和.
【答案】
【详解】所以，
所以，
所以①，
②，
得，
题型二 裂项相消
2023秋·湖南师大附中月考（二）
已知数列满足，当时，.
(1)求数列的通项公式；
(2)证明：.
【答案】(1),(2)证明见解析
【分析】（1）根据题意化简得到，得到数列为等差数列，进而求得数列的通项公式；
（2）由，得到，结合裂项求和及，即可得证.
【详解】（1）解：由，可得，即，
则数列是公差为的等差数列，
又由，可得，则，可得，
所以数列的通项公式是.
（2）解：由，则.
所以
.
因为，所以，
即.
已知，设，证明：.
【详解】解：因为
，
，故
.
已知，设，求数列的前项和.
【答案】
【详解】
，
所以
已知，求证：.
【详解】.
.
另解：
.得证
已知，若，求数列的前n项和
【详解】由，
可得，
则数列的前项和为
.
已知，若，求的前n项和.
【详解】，
所以
.
已知正项数列的前n项和为，且满足，
(1)求
(2)求
【答案】(1);(2)
【分析】(1)先令求出首项，再由数列的递推公式，当时，代入并结合
等差数列的定义和通项公式求出.
(2)由第一问的公式，正好利用分母有理化进行化简抵消即可得出结果
【详解】（1）根据题意可得，当时，，解得，
由，代入得，整理后得
，即，根据等差数列的定义可知，数列
是首项为1，公差为1的等差数列，则，
（2）由(1)可知，
，
已知，数列前项和，记，设数列的前项和为，求证
【解答】，
，，，，，
.
题型三 分组求和
（2023·河北沧州·校考三模）已知，设为数列在区间中的项的个数，求数列前100项的和.
【答案】
【详解】由为数列在区间中的项的个数，
可知，，.
当时，；当时，；
当时，；当时，.
∴.
若数列的前项和为，且，则（ ）
A．684B．682C．342D．341
【答案】B
【分析】根据等比数列求和公式以及并项求和法得出结果.
【详解】，，，，，
所以.
已知，若数列满足，求数列的前项和．
【答案】
【详解】因为，所以，
所以
．
已知，设，数列的前项和为，求.
【答案】
【详解】
.
已知，求满足的最大整数.
【答案】11
【详解】
，
当时，，
当时，，
又易知当时，，故时，和式，
故满足的最大整数为11.
（2023·山东泰安·模拟）已知，求数列的前项和.
【答案】
【详解】，
设，其前n项和为，
所以，①
， ②
①②得
，
所以，
所以当时，，
当时，

，
所以.
（2023·广东二模）已知，若数列满足，求数列的前2n项的和．
【解析】
所以，
所以
，
，
所以数列的前2n项的和．
已知数列的前n项和，且，数列满足，其中．
(1)求和的通项公式；
(2)设，求数列的前20项和．
【答案】(1)，(2)
【分析】（1）根据、累乘法求得和的通项公式；
（2）结合分组求和法、裂项相消求和法求得.
【详解】（1）对于，当时，，
当时，由得，
两式相减得，由于，
所以是首项为，公比为的等比数列，所以.
对于，，
所以，
也符合上式，所以.
（2）当为奇数时，；，
所以.
当为偶数时，；
所以
.
所以.
（2023·吉东北师大附中一模）已知各项均为正数的数列满足：，．
(1)求数列的通项公式；
(2)若，记数列的前项和为，求．
【答案】(1)
(2)
【分析】（1）根据，两边同除从而得到，则得到其通项；
【详解】（1）因为各项为正数，，
所以上式两边同时除以，得，
令，则，即，解得（负值舍去），
所以，又，
所以是以，的等比数列，
故.
（2），
当时，，当时，，当时，，
当时，，根据三角函数周期性知的周期为4，
则
记，为数列的前n项和，已知，．
(1)求，并证明是等差数列；
(2)求．
【答案】(1)，证明见解析；(2)
【详解】（1）解：已知，
当时，，；当时，，，所以．
因为①，所以②．
②－①得，，整理得，，
所以（常数），，
所以是首项为6，公差为4的等差数列．
（2）解：由（1）知，，，．
当n为偶数时，；
当n为奇数时，．
综上所述，.
题型四 倒序相加
（2023·江西南昌·统考三模）“数学王子”高斯是近代数学奠基者之一，他的数学研究几乎遍及所有领域，在数论､代数学､非欧几何､复变函数和微分几何等方面都作出了开创性的贡献.我们高中阶段也学习过很多高斯的数学理论，比如高斯函数､倒序相加法､最小二乘法等等.已知某数列的通项，则（ ）
A．B．C．D．
【答案】D
【分析】分离常数后可得，再利用倒序相加法，即可求解．
【详解】当时，，
，
，
，
，
，即.
（2023·江苏·统考模拟预测）若数列满足，，则的前n项和为 .
【答案】
【分析】利用倒序相加法结合组合数的性质可求的前n项和.
【详解】设的前n项和为，则，
又，
故
，
故
已知函数，则 ；设数列满足，则此数列的前2023项的和为 .
【答案】
【分析】由题意可知，即可根据此关系求出，因为，则，利用倒序相加法求和即可，
【详解】解：已知，
则，
，
所以，
则，
已知数列，
，，
数列的前2023项的和，
且，
两式相加，得
（2023·湖北·统考模拟预测）“数学王子”高斯是近代数学奠基者之一，他的数学研究几乎遍及所有领域，并且高斯研究出很多数学理论，比如高斯函数､倒序相加法､最小二乘法､每一个阶代数方程必有个复数解等.若函数，设，则 .
【答案】46
【分析】先证，由倒序相加法可得通项，然后可解.
【详解】因为函数的定义域为，
设是函数图象上的两点，其中，且，则有，
从而当时，有：，当时，，
，
相加得
所以，又，
所以对一切正整数，有；
故有.
已知函数，若函数，数列为等差数列，，则 ．
【答案】44
【分析】先求得，然后利用倒序相加法求得正确答案.
【详解】由题意，可得，
设等差数列的前项和为，公差为，
则，解得，
则，根据等差中项的性质，可得，
则
，
同理可得，，，，，
∴．