综合解析-京改版八年级数学上册期末专题测评试题 卷（Ⅲ）（含答案详解）

这是一份综合解析-京改版八年级数学上册期末专题测评试题 卷（Ⅲ）（含答案详解），共22页。
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 35分）
一、单选题（5小题，每小题3分，共计15分）
1、如图为了测量B点到河对面的目标A之间的距离，在B点同侧选择了一点C，测得∠ABC＝65°，∠ACB＝35°，然后在M处立了标杆，使∠MBC＝65°，∠MCB＝35°，得到△MBC≌△ABC，所以测得MB的长就是A，B两点间的距离，这里判定△MBC≌△ABC的理由是（ ）
A．SASB．AAAC．SSSD．ASA
2、如图，与交于点，，则的度数为（ ）
A．B．C．D．
3、四个数0，1，中，无理数的是（ ）
A．B．1C．D．0
4、如图，Rt△ACB中，∠ACB=90°，△ACB的角平分线AD，BE相交于点P，过P作PF⊥AD交BC的延长线于点F，交AC于点H，则下列结论：①∠APB=135°； ②AD=PF+PH；③DH平分∠CDE；④S四边形ABDE=S△ABP；⑤S△APH=S△ADE，其中正确的结论有（ ）个
A．2B．3C．4D．5
5、能说明“锐角，锐角的和是锐角”是假命题的例证图是（ ）．
A．B．
C．D．
二、多选题（5小题，每小题4分，共计20分）
1、下列式子是分式的有（ ）
A．B．C．D．
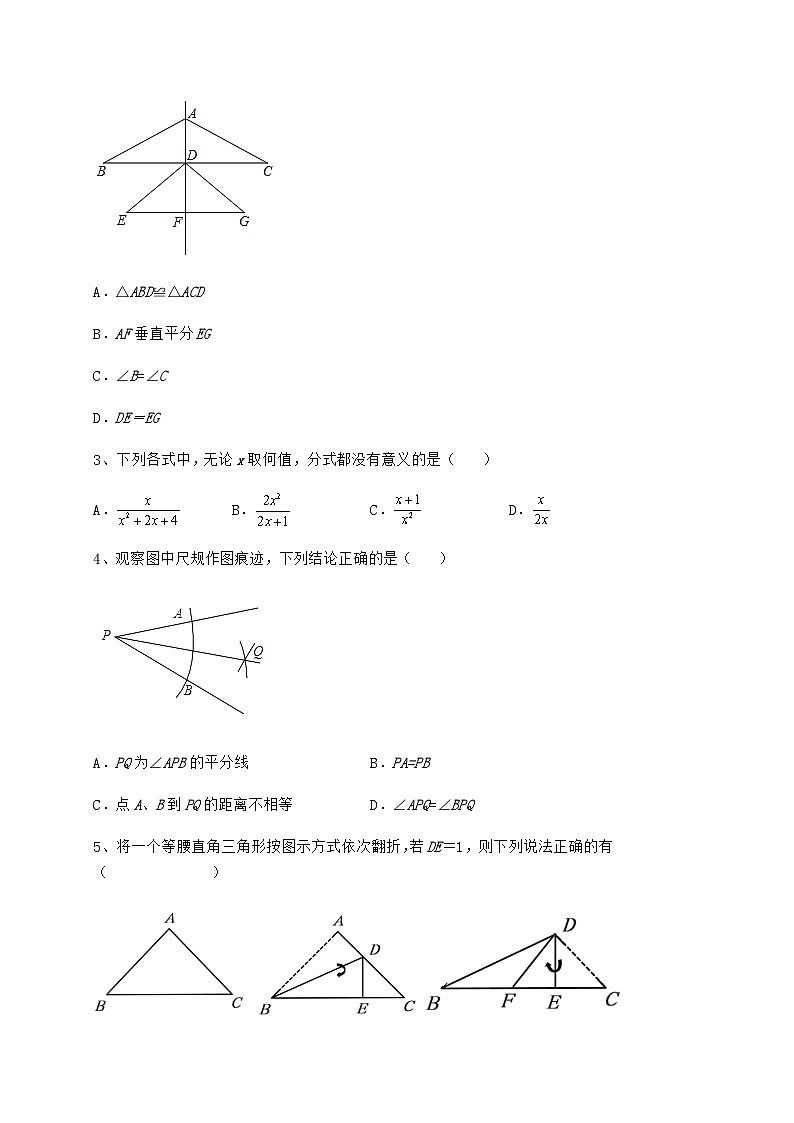
2、如图是一个风筝的图案，它是以直线AF为对称轴的轴对称图形，下列结论中一定成立的是（ ）
A．△ABD≌△ACD
B．AF垂直平分EG
C．∠B=∠C
D．DE＝EG
3、下列各式中，无论x取何值，分式都没有意义的是（ ）
A．B．C．D．
4、观察图中尺规作图痕迹，下列结论正确的是（ ）
A．PQ为∠APB的平分线B．PA=PB
C．点A、B到PQ的距离不相等D．∠APQ=∠BPQ
5、将一个等腰直角三角形按图示方式依次翻折，若DE＝1，则下列说法正确的有（ ）
A．DF平分∠BDEB．BC长为
C．△B FD是等腰三角形D．△CED的周长等于BC的长．
第Ⅱ卷（非选择题 65分）
三、填空题（5小题，每小题5分，共计25分）
1、若的整数部分是，小数部分是，则__．
2、方程的解是______．
3、如图，则∠A+∠B+∠C+∠D+∠E的度数是__．
4、若一个分数的分子、分母同时加1，得；若分子、分母同时减2，则得，这个分数是______．
5、如图，等边ABC的边长为6，点D是AB上一动点，过点D作DEAC交BC于E，将BDE沿着DE翻折得到，连接，则的最小值为________．
四、解答题（5小题，每小题8分，共计40分）
1、如图，点D，E在△ABC的边BC上，AB＝AC，AD＝AE，求证：BD＝CE．
2、解方程：
（1） （2）
3、计算：
（1）
（2）
4、（1）计算：（﹣2）2﹣（π﹣3.14）0+；
（2）化简：（x﹣3）（x+3）+x（2﹣x）．
5、在计算的值时，小亮的解题过程如下：
解：原式
①
②
③
④
（1）老师认为小亮的解法有错，请你指出：小亮是从第_________步开始出错的；
（2）请你给出正确的解题过程．
-参考答案-
一、单选题
1、D
【解析】
【分析】
利用全等三角形的判定方法进行分析即可．
【详解】
解：在△ABC和△MBC中，
∴△MBC≌△ABC（ASA），
故选：D．
【考点】
本题考查了全等三角形的应用，熟练掌握三角形全等的判定定理是解题的关键．
2、A
【解析】
【分析】
先根据三角形的内角和定理可求出，再根据平行线的性质即可得．
【详解】
故选：A．
【考点】
本题考查了三角形的内角和定理、平行线的性质，熟记平行线的性质是解题关键．
3、A
【解析】
【分析】
分别根据无理数、有理数的定义即可判定选择项．
【详解】
0，1，是有理数，是无理数，
故选A．
【考点】
此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，，0.8080080008…（每两个8之间依次多1个0）等形式．
4、B
【解析】
【分析】
①正确．利用三角形内角和定理以及角平分线的定义即可解决问题．
②正确．证明△ABP≌△FBP，推出PA=PF，再证明△APH≌△FPD，推出PH=PD即可解决问题．
③错误．利用反证法，假设成立，推出矛盾即可．
④错误，可以证明S四边形ABDE=2S△ABP．
⑤正确．由DH∥PE，利用等高模型解决问题即可．
【详解】
解：在△ABC中，AD、BE分别平分∠BAC、∠ABC
∵∠ACB=90°
∴∠A+∠B=90°
又∵AD、BE分别平分∠BAC、∠ABC
∴∠BAD+∠ABE=（∠A+∠B）=45°
∴∠APB=135°，故①正确
∴∠BPD=45°
又∵PF⊥AD
∴∠FPB=90°+45°=135°
∴∠APB=∠FPB
又∵∠ABP=∠FBP
BP=BP
∴△ABP≌△FBP（ASA）
∴∠BAP=∠BFP，AB=FB，PA=PF
在△APH和△FPD中
∴△APH≌△FPD（ASA）
∴PH=PD
∴AD=AP+PD=PF+PH．故②正确
∵△ABP≌△FBP，△APH≌△FPD
∴S△APB=S△FPB，S△APH=S△FPD，PH=PD
∵∠HPD=90°
∴∠HDP=∠DHP=45°=∠BPD
∴HD∥EP
∴S△EPH=S△EPD
∴S△APH=S△AED，故⑤正确
∵S四边形ABDE=S△ABP+S△AEP+S△EPD+S△PBD
=S△ABP+（S△AEP+S△EPH）+S△PBD
=S△ABP+S△APH+S△PBD
=S△ABP+S△FPD+S△PBD
=S△ABP+S△FBP
=2S△ABP，故④不正确
若DH平分∠CDE，则∠CDH=∠EDH
∵DH∥BE
∴∠CDH=∠CBE=∠ABE
∴∠CDE=∠ABC
∴DE∥AB，这个显然与条件矛盾，故③错误
故选B．
【考点】
本题考查了角平分线的判定与性质，三角形全等的判定方法，三角形内角和定理，三角形的面积等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．
5、C
【解析】
【分析】
先将每个图形补充成三角形，再利用三角形的外角性质逐项判断即得答案．
【详解】
解：A、如图1，∠1是锐角，且∠1=，所以此图说明“锐角，锐角的和是锐角”是真命题，故本选项不符合题意；

B、如图2，∠2是锐角，且∠2=，所以此图说明“锐角，锐角的和是锐角”是真命题，故本选项不符合题意；
C、如图3，∠3是钝角，且∠3=，所以此图说明“锐角，锐角的和是锐角”是假命题，故本选项符合题意；
D、如图4，∠4是锐角，且∠4=，所以此图说明“锐角，锐角的和是锐角”是真命题，故本选项不符合题意．
故选：C．
【考点】
本题考查了真假命题、举反例说明一个命题是假命题以及三角形的外角性质等知识，属于基本题型，熟练掌握上述基本知识是解题的关键．
二、多选题
1、CD
【解析】
【分析】
根据分式定义：如果A、B(B不等于零)表示两个整式，且B中含有字母，那么式子叫做分式，其中A称为分子，B称为分母，据此判断即可．
【详解】
解：A、分母中没有字母，不是分式，不符合题意；
B、分母中没有字母，不是分式，不符合题意；
C、，是分式，符合题意；
D、，是分式，符合题意；
故选：CD．
【考点】
本题考查了分式的定义，熟知分式的概念是解本题的关键．
2、ABC
【解析】
【分析】
认真观察图形，根据轴对称图形的性质得选项A、B、C都是正确的，没有理由能够证明△DEG是等边三角形．
【详解】
解：A、因为此图形是轴对称图形，则△ABD≌△ACD正确；
B、对称轴垂直平分对应点连线，正确；
C、由三角形全等可知，∠B＝∠C，正确；
D、题目中没有60°条件，不能判断是等边三角形，故不能得到DE＝EG错误．
故选：ABC．
【考点】
本题考查了轴对称的性质；解决此题要注意，不要受图形误导，要找准各选项正误的具体原因是正确解答本题的关键．
3、BCD
【解析】
【分析】
根据分式有意义的条件分析四个选项哪个方式分母不为零，进而可得答案．
【详解】
A、 ， ，则，无论 取何值，分式都有意义，故此选项正确；
B、当时，分式分母=0，分式无意义，故此选项错误；
C、当时，分式分母=0，分式无意义，故此选项错误；
D、当时，分式分母=0，分式无意义，故此选项错误．
故选BCD．
【考点】
此题主要考查了分式有意义的条件，关键是掌握分式有意义的条件是分母不等于零．
4、ABD
【解析】
【分析】
根据图形的画法得出PQ是∠APB的角平分线，再根据尺规作图的画法结合等腰三角形的性质逐项分析四个选项即可得出结论．
【详解】
解：根据尺规作图的画法可知：PQ是∠APB的角平分线．
A、PQ是∠APB的平分线，原选项正确；
B、根据角平分线的作法得PA=PB，原选项正确；
C、∵PA=PB，PQ是∠APB的平分线，∴PQ⊥AB，PQ平分AB，∴点A、B到PQ的距离相等，原选项错误；
D、∵PQ是∠APB的平分线，∴∠APQ=∠BPQ，原选项正确．
故选：ABD．
【考点】
本题考查了尺规作图中的作角的平分线以及等腰三角形的性质，本题属于基础题，难度不大，牢记尺规作图的方法和步骤是关键．
5、BCD
【解析】
【分析】
由和等腰直角三角形,可推出，进一步由角度关系得到，结合，可得到，即可判断出A、C是否正确；通过分析可以得到,从而在中，得到长度，进一步求得的周长和BC的长度，即可判断B、D是否正确．
【详解】
解：∵是等腰直角三角形，且
∴
∵折叠
∴
∴ ，
∴
∵折叠
∴
∴
∴，
∴
∵
∴
∴不是的角平分线，选项A错误
∵
∴
∴是等腰三角形，选项C正确．
∵
∴
∴
∵
∴
∴
∴
∵
∴
又∵
∴
∴的周长等于的长，所以选项B、D正确
故选：BCD
【考点】
本题考查等腰三角形的性质，直角三角形互余，三角形外角性质以及三角形全等性质等知识点，根据知识点解题是关键．
三、填空题
1、．
【解析】
【分析】
先确定出的范围，即可推出a、b的值，把a、b的值代入求出即可．
【详解】
解：，
，，
．
故答案为：．
【考点】
考查了估算无理数的大，解此题的关键是确定的范围8