


中考数学二轮重难专题研究 微专题 最值问题(课件)
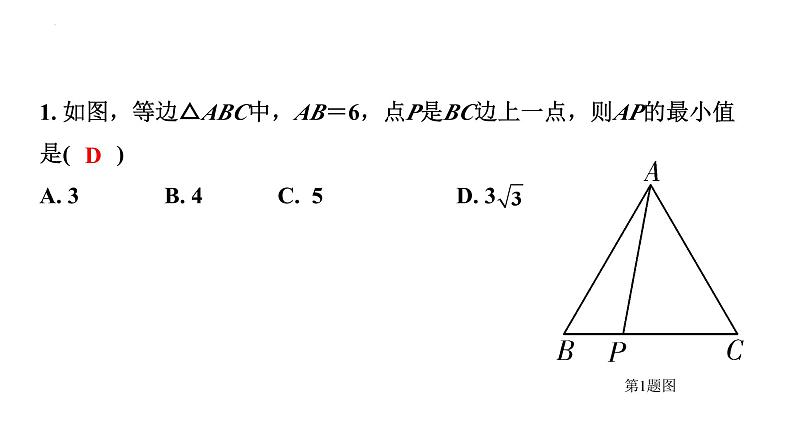
展开1. 如图,等边△ABC中,AB=6,点P是BC边上一点,则AP的最小值是( ) A. 3 B. 4 C. 5 D. 3
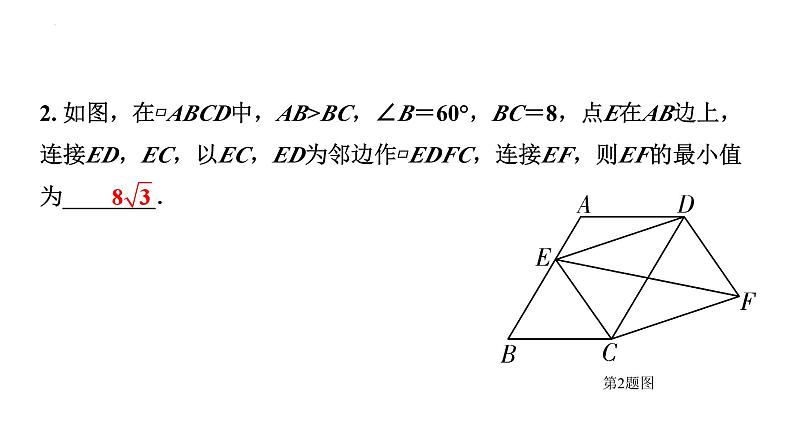
2. 如图,在▱ABCD中,AB>BC,∠B=60°,BC=8,点E在AB边上,连接ED,EC,以EC,ED为邻边作▱EDFC,连接EF,则EF的最小值为________.
如图①,已知点A、点B是平面内固定的两点,AB=m,点C是同一平面内一动点且BC=n(m>n),连接AC、BC.1. 如图①,在△ABC中,∵AC+BC > AB,∴当点A,C,B三点共线 时,如图②,AC+BC的值最小,最小值为AC+BC=AB=m;
类型二 利用三边关系及共线求最值
2. 如图①,在△ABC中,∵AC>AB-BC,∴当点A,C,B三点共线时,如图②,AC的值最小,最小值为AC=AB-BC=m-n.
3. 如图①,在△ABC中,∵AC
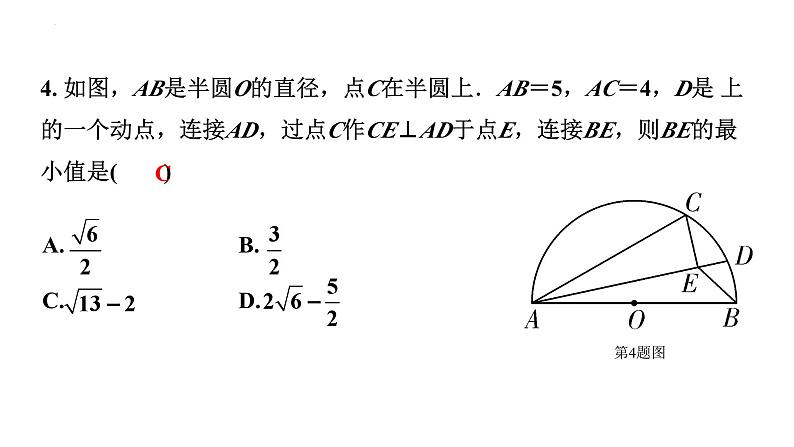
4. 如图,AB是半圆O的直径,点C在半圆上.AB=5,AC=4,D是 上的一个动点,连接AD,过点C作CE⊥AD于点E,连接BE,则BE的最小值是( )
A. B. C. D.
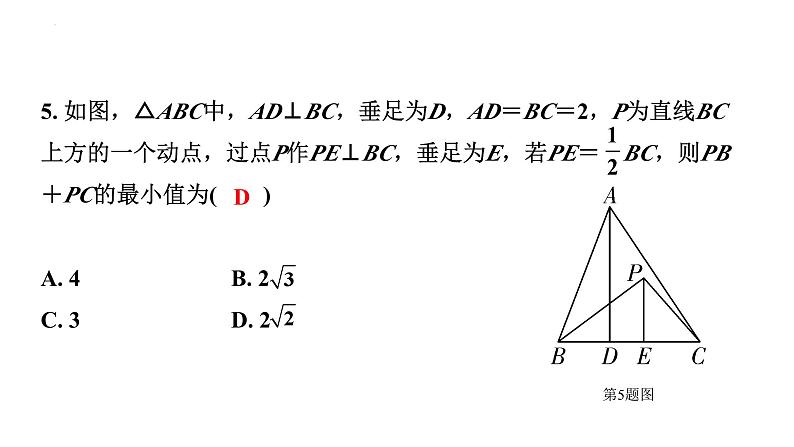
5. 如图,△ABC中,AD⊥BC,垂足为D,AD=BC=2,P为直线BC上方的一个动点,过点P作PE⊥BC,垂足为E,若PE= BC,则PB+PC的最小值为( )A. 4 B. 2C. 3 D. 2
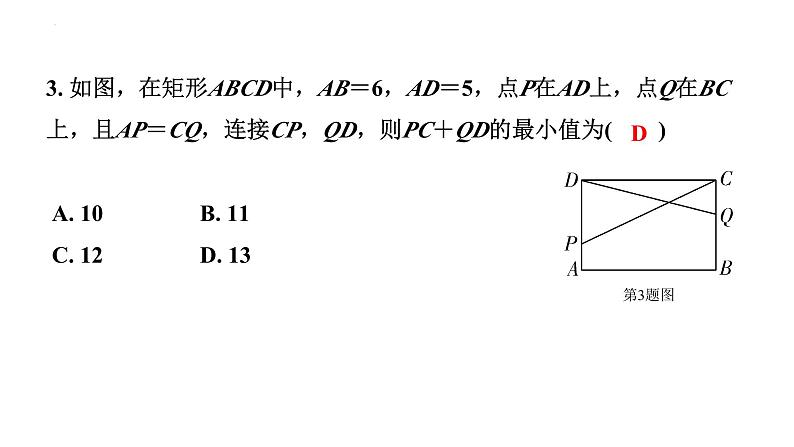
1. “一线两点”型(一个动点+两个定点)① 异侧线段和最小值问题:两定点A、B位于直线l异侧,在直线l上找一点P,使PA+PB值最小.解决思路:根据两点之间线段最短,PA+PB的最小值即为线段AB的长.连接AB交直线l 于点P,点P即为所求.
类型三 利用两点之间线段最短求最值
② 同侧线段和最小值问题:两定点A、B位于直线l同侧,在直线l上找一点P,使得PA+PB值最小.解决思路:将两定点同侧转化为异侧问题,同①即可解决.也可作点B关于l的对称点B′,连接AB′.
2. “一点两线”型(两个动点+一个定点)周长最小问题:点P是∠AOB内部的一定点,在OA上找一点M,在OB上找一点N,使得△PMN周长最小.解决思路:要使△PMN周长最小,即PM+PN+MN值最小.根据两点之间线段最短,将三条线段转化到同一直线上即可.
6. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,AD平分∠CAB交BC于点D,E、F分别是AD,AC边上的动点,则CE+EF的最小值为( ) A. B. C. D.
7. 如图,在等腰△ABC中,AB=BC=4,∠ABC=90°,点D在边BC上且CD=1,点E,F分别为边AB,AC上的动点,连接DE,EF,DF,得到△DEF,则△DEF周长的最小值为( ) A. B. C. D.
8. (2023连云港)如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( ) A. 3 B. 4 C. 5 D. 6
9. 如图,等边△ABC中,BD⊥AC于D,AD=3.5 cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2 cm,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为( ) A. 3 cm B. 4 cm C. 5 cm D. 6 cm
10. 如图,四边形ABCD中,∠A=∠C=90°,点M、N分别是BC、AB边上的动点,∠B=56°,当△DMN的周长取最小值时,则∠MDN的度数是( ) A. 124° B. 68° C. 60° D. 56°
1. 圆中最长的弦为直径:已知点A、B为⊙O上两动点,连接AB,则当AB过圆心O时,AB取最大值;2. 已知平面内一定点D和⊙O上一动点E的所有连线中,当连线过圆心O时,线段DE有最大(小)值(应用依据:三角形三边关系).具体分以下三种情况讨论(设点O与点D之间的距离为d,⊙O的半径为r):
类型四 点圆问题求最值
11. 如图,线段AB=6,点C为线段AB外一动点,∠ACB=45°,连接AC,BC,M,N分别为AB,BC的中点,则线段MN的最大值为( ) A. 3 B. 4 C. 3 D. 3+
12. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AB=5,点D是边BC上一动点,连接AD,在AD上取一点E,使∠DAC=∠DCE,连接BE,则BE的最小值为( ) A. B. C. D.
13. 如图,在Rt△ABC中,∠ACB=90°,BC=4,AC=10,点D是AC上的一个动点,以CD为直径作⊙O,连接BD交⊙O于点E,则AE的最小值为________.
1. 如图,AB为⊙O的一条定弦,点C为AB一侧弧上一动点.(1)如图①,点C在优弧 上,当CH⊥AB且CH过圆心O时,线段CH即为点C到弦AB的最大距离,此时S△ABC最大;(2)如图②,点C在劣弧 上,当CH⊥AB且圆心O在CH的延长线上时,线段CH即为点C到弦AB的最大距离,此时S△ABC最大.
类型五 线圆问题求最值
2. 如图,⊙O与直线l相离,点P是⊙O上的一个动点,设圆心O到直线l的距离为d,⊙O的半径为r,则点P到直线l的最小距离是d-r(如图③),最大距离是d+r(如图④).
14. 如图,AB是⊙O的弦,C是优弧 上一点,连接AC、BC,若⊙O的半径为4,∠ACB=60°,则△ABC面积的最大值为_______.
15. 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=8,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,求线段AF的最小值.
解:如解图,由题知CD=DF=DB,∴点F在以点D为圆心,以BD为半径的圆上运动,
连接AD交⊙D于点F′,此时AF最小,
中考数学复习重难突破微专题(十三)直线型最值问题课件: 这是一份中考数学复习重难突破微专题(十三)直线型最值问题课件,共25页。
中考数学复习重难突破微专题(十一)隐形圆问题课件: 这是一份中考数学复习重难突破微专题(十一)隐形圆问题课件,共27页。
中考数学复习微专题七代数最值问题模型二建立函数模型求最值课件: 这是一份中考数学复习微专题七代数最值问题模型二建立函数模型求最值课件,共9页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。












