






中考数学二轮重难专题研究 专题三 函数的实际应用(课件)
展开时间为x(小时),旅游中巴车距离乙地的路程为y1(千米),客车在遇到旅游团前离开乙地的路程为y2(千米).(1)若v=80千米/时,①y1与x的函数表达式为_________________;
①【思维教练】利用路程=速度×时间求解.
y1=200-50x;
②求y2与x的函数表达式,并写出x的取值范围;.
②【思维教练】利用路程=速度×时间,注意客车与中巴车行驶时间的关系,求x的取值范围时注意区分是在y2的情况下求x的取值范围.
②y2=80(x-1.6),即y2=80x-128.由题可知200-80=120(千米),∵120÷80=1.5(小时),1.6+1.5=3.1(小时),∴x的取值范围是1.6≤x≤3.1;
(2)设旅游团从甲地到乙地所用的总时间为T(小时),求T(小时)与v(千米/时)的函数关系式(不写v的取值范围);
【思维教练】想一想总时间T包含哪几段呢?
(3)旅游团要求到达时间比按原来的旅游中巴正常到达乙地的时间最多晚1个小时,问客车返回乙地的车速至少为每小时多少千米?
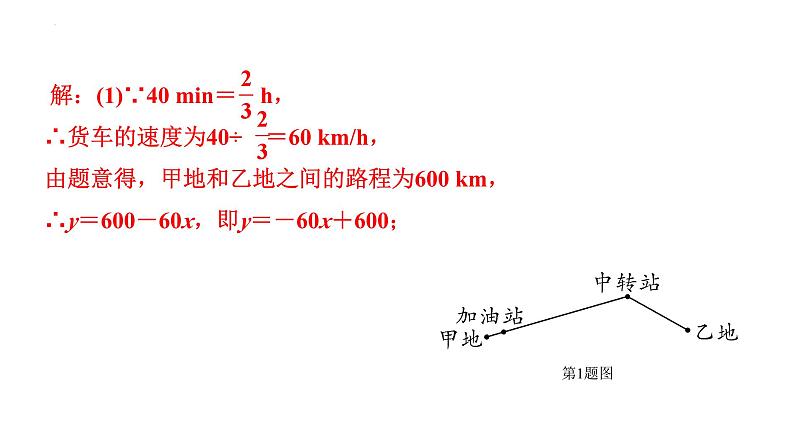
1. 一辆快递货车按如图所示的路线匀速从甲地开往乙地运送货物,甲、乙两地到中转站的路程分别为400 km和200 km.货车从甲地开出40 min后,到达距其40 km的加油站加油(加油时间忽略不计),后途经中转站开往乙地.设货车行驶时间为x h,货车距乙地的路程为y km.(1)求y与x的函数关系式(不写x的取值范围);
解:(1)∵40 min= h,∴货车的速度为40÷ =60 km/h, 由题意得,甲地和乙地之间的路程为600 km,∴y=600-60x,即y=-60x+600;
(2)当货车与中转站之间的路程为100 km时,求x的值;
(3)当货车到达中转站时,接到通知,要求比原定到达乙地的时间提前40 min,求货车提速后的平均速度.
2. (2021河北九地市二模)甲、乙两车在连通A、B、C三地的公路上行驶,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1小时后,按原路原速返回到C地,在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:(1)求甲、乙两车的速度;
(2)求乙车从B地返回到C地的过程中,y与x之间的函数关系式;
(3)当甲、乙两车行驶到距B地的路程相等时,甲、乙两车距B地的路程是多少?
∵图象经过(8,200),(6,0)两点,∴ 解得∴y2=100x-600,∴甲车距B地的距离y与行驶时间x之间的函数关系式为y= 联立 解得y= 千米.
联立 解得y=100千米.∴当甲、乙两车行驶到距B地的路程相等时,甲、乙两车距B地的路程是 千米或100千米.
(10年3考:2023.26,2022.24,2022.24)
例 某公司为了宣传一种新产品,在某地先后举行18场产品促销会,已知该产品每台成本为4万元,设第x场产品的销售量为y(台),在销售过程中获得以下信息:信息1:已知第一场销售产品38台,然后每增加一场,产品就少卖出2台;信息2:产品的每场销售单价p(万元)由基本价和浮动价两部分组成,
其中基本价保持不变,第1场—第10场浮动价与销售场次x成正比,第11场—第18场浮动价与销售场次x成反比,经过统计,得到如下数据:
(1)求y与x之间的函数关系式;
【思维教练】根据信息1求关系式,注意是从第二场开始每场减少2台.
解:(1)由题意可得,y与x的函数关系式为y=38-2(x-1)=-2x+40;
(2)求销售单价p与销售场次x之间的函数关系式;
【思维教练】“成正比”转化为一次函数,“成反比”转化为反比例函数,利用待定系数法求解.
②∵第11场—第18场浮动价与销售场次x成反比,由①知b=4,∴设p与x的函数关系式为p= +4,依题意得7= +4,解得m=45,∴p= +4(11≤x≤18);综上所述,销售单价p与销售场次x之间的函数关系式为p= ;
【思维教练】已知函数值求自变量时可将问题转化为解方程.
(3)当产品销售单价为6.5万元时,求销售场次是第几场?
(4)在这18场产品促销会中,哪一场获得的利润最大,最大利润是多少?(结果保留整数)
②当11≤x≤18时,w=( +4-4)(-2x+40)= -90,∵1800>0,∴w随x的增大而减小,∴当x=11时,w最大,最大利润w= -90≈74(万元),∵50<74,∴在这18场产品促销会中,第11场获得的利润最大,最大利润约为74万元 .
1. (2021石家庄模拟)某公司购进一批受环境影响较大的商品,需要在特定的环境中才能保存.已知该商品成本y(元/件)与保存的时间第x天之间的关系满足y=x2-4x+100,该商品售价p(元/件)与保存的时间第x天之间满足一次函数关系,其对应数据如下表:
(1)求商品的售价p(元/件)与保存的时间第x天之间的函数关系式;
(2)求保存第几天时,该商品不赚也不亏;
(2)依题意,得方程8x+208=x2-4x+100.整理方程,得 x2-12x-108=0.解得x1=18,x2=-6(不合题意,舍去).∴该商品保存第18天时,不赚也不亏;
(3)请你帮该公司确定该商品在哪一天卖出,每件商品能获得最大利润?此时每件商品的售价是多少?
(3)设每件商品所获利润为w元,依题意,得w=8x+208-(x2-4x+100)=-x2+12x+108=-(x-6)2+144,∵-1<0,∴当x=6时,w最大=144,∴p=8x+208=8×6+208=256(元).∴该商品在第6天卖出时,每件商品能获得最大利润,此时每件商品的售价为256元.
2. 某水杯零售店购进某品牌水杯的进价为a元/个,售价为x元/个(a≤x≤48).下面是水杯零售店在销售该品牌水杯一段时间后销售情况的反馈:
设该品牌水杯每月的销售量为y(个),售价为x(元/个).
(1)求a的值,并写出y与x之间的函数关系式(注明自变量x的取值范围);
(2)若水杯零售店销售该品牌水杯每月获得的利润为W(元),求每月获得的最大利润;
(2)根据题意,得W=(x-20)(-10x+800)=-10(x-50)2+9000,∵-10<0,销售单价不能超过48元/个,即当20≤x≤48时,W随x的增大而增大,∴当x=48时,W有最大值,最大值为8960.答:当售价为48元/个时,每月获得的利润最大,最大利润为8960元;
(3)由于市场原因,该品牌水杯进价降低为n元/个,售价为x元/个(n≤x≤48).该水杯零售店在2月份仍然按照之前的销售量与售价的关系进行销售,若要使这个月销售该品牌水杯获得的利润G(元)随售价x(元/个)的增大而增大,求n的取值范围.
类型三 实物模型 (2022.26)
例 (2021广西北部湾经济区)2022年北京冬奥会即将召开,激起了人们对冰雪运动的极大热情.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=- x2+ x+1近似表示滑雪场地上的一座小山坡,某运动员从点O正上方4米处的A点滑出,滑出后沿一段抛物线C2:y=- x2+bx+c运动.
(1)当运动员运动到离A处的水平距离为4米时,离水平线的高度为8米,求抛物线C2的函数解析式(不要求写出自变量x的取值范围);
【思维教练】用待定系数法求解.
(2)在(1)的条件下,当运动员运动的水平距离为多少米时,运动员与小山坡的竖直距离为1米?
【思维教练】用含x的代数式表示运动员与小山坡的竖直距离,由已知列等式,求解一元二次方程即可.
(3)当运动员运动到坡顶正上方,且与坡顶距离超过3米时,求b的取值范围.
【思维教练】列一元一次不等式求解即可.
1. (2021石家庄28中二模)小亮和小明在篮球场练习投篮,小亮投篮时篮球出手的高度是1.7米,篮球的运行路线是抛物线的一部分,篮球运行的水平距离为3米时达到最高点,最高点的高度是3.5米,篮筐的高度是3.05米,结果小亮恰好命中篮筐,建立如图所示的平面直角坐标系(篮球和篮筐均看作一个点),y轴经过抛物线的顶点,解答下列问题.(1)求小亮投篮时篮球运行路线所在抛物线的解析式;
解:(1)∵小亮投篮时篮球的运行路线是抛物线物一部分,该抛物线对称轴是y轴,最高点的纵坐标是3.5,∴可设其解析式为y=ax2+3.5,∵抛物线经过点(-3,1.7),∴1.7=a×(-3)2+3.5,解得a=-0.2,∴小亮投篮时篮球运行路线所在抛物线的解析式为y=-0.2x2+3.5;
(2)求小亮投篮时与篮筐的水平距离L;
(2)令-0.2x2+3.5=3.05,解得x=1.5或x=-1.5(舍去),∵3+1.5=4.5米,∴小亮投篮时与篮筐的水平距离L为4.5米;
(3)小亮投篮后篮球被篮筐弹了出来,恰被离篮筐水平距离为5米处的小明跳起来接住.已知篮球弹出后运行路线也是抛物线的一部分(两抛物线在同一平面内),运行的水平距离为2米时到达最高点,小明接球的高度为2.3米.①求篮球弹出后最高点的高度;
(3)①∵篮球弹出后运行的水平距离为2米时到达最高点,且篮筐到y轴的距离为1.5米,∴篮球弹出后运行路线所在抛物线的对称轴是直线x=-0.5,故可设该抛物线的解析式为y=a′(x+0.5)2+k,
∵小明到篮筐的水平距离为5米,篮筐到y轴的距离为1.5米,∴小明到y轴的距离为3.5米.故抛物线y=a′(x+0.5)2+k经过点(-3.5,2.3),又知抛物线经过点(1.5,3.05),∴ 解得 即y=-0.15(x+0.5)2+3.65,∴篮球弹出后最高点的高度为3.65米;
②若小明不接球,让篮球自由落地,则落地点到篮筐的水平距离是多少米?(结果保留根号)
2. (2021石家庄43中三模)用各种盛水容器可以制作精致的家用流水景观(如图①).科学原理:如图②,始终盛满水的圆柱体水桶水面离地面的高度为H(单位: cm),如果在离水面竖直距离为h(单位:cm)的地方开大小合适的小孔,那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位:cm)与h的关系式为s2=4h(H-h).
应用思考:现用高度H为20 cm的圆柱体塑料水瓶做相关研究,水瓶直立地面,通过连续注水保证它始终盛满水,在离水面竖直距离h cm处开一个小孔. (1)写出s2与h的关系式,并求出当h为何值时,射程s有最大值,最大射程是多少?
解:(1)∵s2=4h(H-h),∴当H=20 cm时,s2=4h(20-h)=-4(h-10)2+400.∵-4<0,∴当h=10时,s2有最大值400 cm2,此时S=20 cm.∴当h=10 cm时,射程S有最大值,最大射程是20 cm;
(2)当小孔射出水的射程为10 cm时,求小孔离水面的竖直距离是多少?
(3)在侧面开两个小孔,这两个小孔离水面的竖直距离分别为a,b,要使两孔射出水的射程相同,请直接写出a,b之间满足的关系.
(3)a=b或a+b=20.
【解法提示】∵s2=4h(20-h),设存在a,b,使两孔射出水的射程相同,则有:4a(20-a)=4b(20-b),∴20a-a2=20b-b2,∴a2-b2=20a-20b,∴(a+b)(a-b)=20(a-b),∴(a-b)(a+b-20)=0,∴a-b=0或a+b-20=0,∴a=b或a+b=20.
类型四 几何图形问题 (2023.23)
例 (2021河北逆袭卷)如图是一种画正方形的工具板,工具板长为210 mm,上面依次排列着大小不等的五个正方形,正方形边长从左到右依次减少2 mm,其中最左侧正方形的边长为x mm,左右两端的正方形的边距工具板边缘都为15 mm,相邻两个正方形的间距均为y mm.(1)求y与x之间的函数关系式;
【思维教练】求函数关系式一般有两种思路:①明确函数类型并且已知图象上点坐标的,可用待定系数法求解;②不知道函数类型,联想函数与方程的关系,通过列方程求解.
(2)当相邻两个正方形的间距为20 mm时,求最大正方形的边长;
【思维教练】分清楚“间距”是指的自变量还是函数值,代入解方程求解.
(3)如果最大正方形的边长不大于30 mm,求相邻两个正方形间距的最小值.
【思维教练】函数中求最值问题,都是利用函数的增减性,要注意自变量的取值范围.
(3)对于一次函数y=- x+50,∵- <0,∴y随x的增大而减小,∵最大正方形的边长不大于30 mm,即8
(1)求出每个小正方块和大正方块的重量;
(2)若只悬挂一种正方块,分别求出测力计示数F与悬挂小正方块的数量x小,悬挂大正方块的数量x大之间的函数关系式;
(2)由题意得,F小=0.2x小+0.1,F大=0.3x大+0.1;D
(3)为确保测力计示数在量程范围内,且悬挂正方块的总数量为20个,则最多悬挂大正方块的数量是多少?
(3)设悬挂大正方块m个,则悬挂小正方块(20-m)个,由题意得,F总=0.3 m+0.2(20-m)+0.1=0.1m+4.1,∵F总≤5,∴0.1m+4.1≤5,解得m≤9,∴m的最大值为9,∴最多悬挂大正方块的数量是9个.
2. (2021苏州)如图①,甲、乙都是高为6米的长方体容器,容器甲的底面ABCD是正方形,容器乙的底面EFGH是矩形.如图②,已知正方形ABCD与矩形EFGH满足如下条件:正方形ABCD外切于一个半径为5米的圆O,矩形EFGH内接于这个圆O,EF=2EH.(1)求容器甲、乙的容积分别为多少立方米?
解:(1)由题知,正方形ABCD的边长AB=10,∴容器甲的容积为102×6=600立方米.如解图,连接FH,
∵∠FEH=90°,∴FH为⊙O的直径.在Rt△EFH中, EF=2EH,FH=10,根据勾股定理,得EF=4,EH=2,∴容器乙的容积为2×4×6=240立方米;
(2)现在我们分别向容器甲、乙同时持续注水(注水前两个容器是空的),一开始注水流量均为25立方米/小时,4小时后,把容器甲的注水流量增加a立方米/小时,同时保持容器乙的注水流量不变,继续注水2小时后,把容器甲的注水流量再一次增加50立方米/小时,同时容器乙的注水流量仍旧保持不变,直到两个容器的水位高度相同,停止注水.
在整个注水过程中,当注水时间为t时,我们把容器甲的水位高度记为h甲,容器乙的水位高度记为h乙,设h乙-h甲=h,已知h(米)关于注水时间t(小时)的函数图象如图③所示,其中MN平行于横轴.根据图中所给信息,解决下列问题:
中考数学二轮重难专题研究 专题二 函数图像与性质综合题 课件: 这是一份中考数学二轮重难专题研究 专题二 函数图像与性质综合题 课件,共51页。PPT课件主要包含了例题图,第1题图,第2题图,第2题解图②,思路分析,A的横坐标,点A的横坐标为-2,补画出y轴,如解图,P会落在哪个台阶上等内容,欢迎下载使用。
中考数学二轮重难专题研究 微专题 最值问题(课件): 这是一份中考数学二轮重难专题研究 微专题 最值问题(课件),共26页。PPT课件主要包含了第1题图,第2题图,第3题图,第4题图,第5题图,第6题图,第7题图,第8题图,第9题图,第10题图等内容,欢迎下载使用。
中考数学复习重难题型八函数的实际应用课件: 这是一份中考数学复习重难题型八函数的实际应用课件,共36页。












