




中考数学二轮复习 专题突破课件 专题七 反比例函数综合
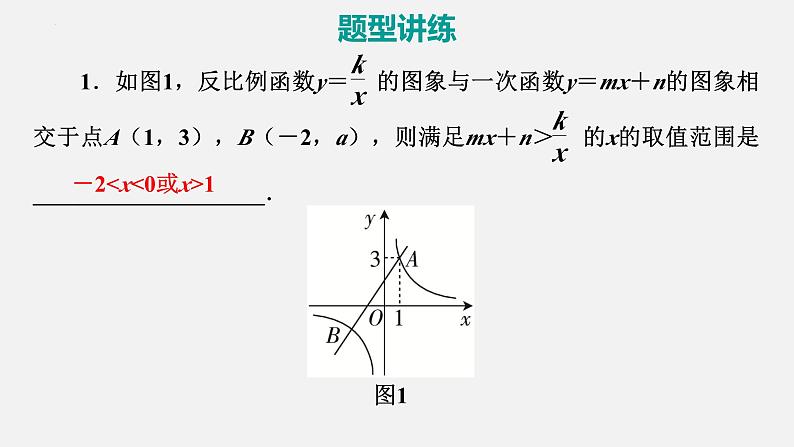
展开1.如图1,反比例函数y= 的图象与一次函数y=mx+n的图象相交于点A(1,3),B(-2,a),则满足mx+n> 的x的取值范围是____________________.
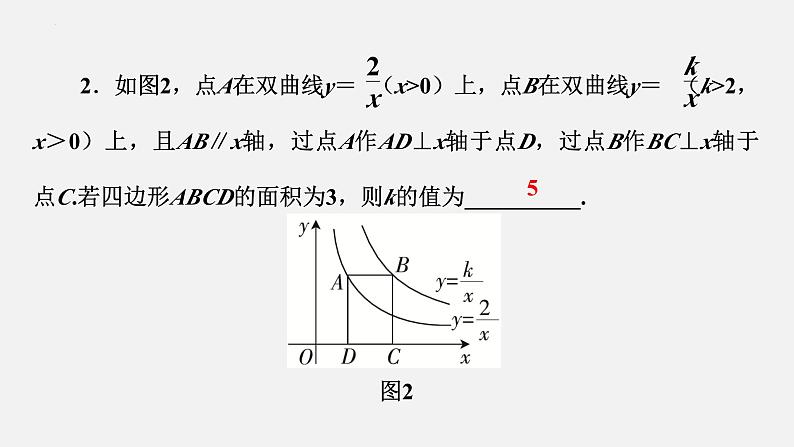
2.如图2,点A在双曲线y= (x>0)上,点B在双曲线y= (k>2,x>0)上,且AB∥x轴,过点A作AD⊥x轴于点D,过点B作BC⊥x轴于点C.若四边形ABCD的面积为3,则k的值为__________.图2
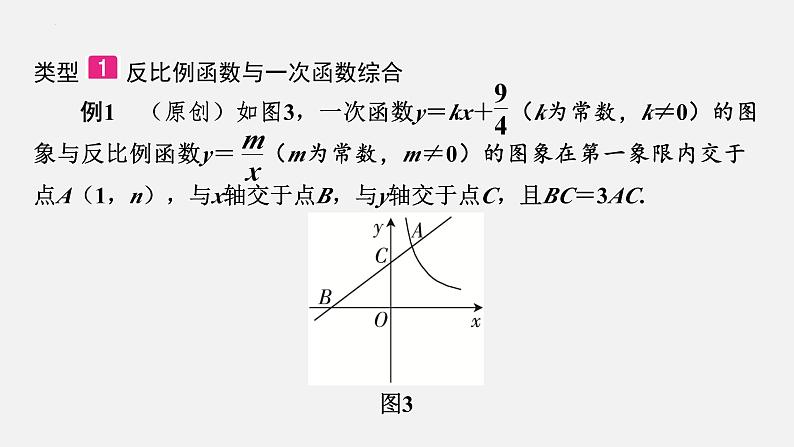
类型 反比例函数与一次函数综合例1 (原创)如图3,一次函数y=kx+ (k为常数,k≠0)的图象与反比例函数y= (m为常数,m≠0)的图象在第一象限内交于点A(1,n),与x轴交于点B,与y轴交于点C,且BC=3AC.图3
(1)求一次函数和反比例函数的解析式;
解:∵BC=3AC,点A的横坐标为1,∴点B的横坐标为-3.∴B(-3,0).
(2)结合一次函数和反比例函数在第一象限内的图象,直接写出关于x的不等式 在x>0时的解集;
(3)如图4,点M为线段AB上一点(不与点A,B重合),当S△BOM=2S△AOM时,求点M的坐标;
解:如答图1,过点M作MG⊥x轴于点G,过点A作AH⊥x轴于点H.
由(1)知A(1,3),B(-3,0),
∵S△AOB=S△BOM+S△AOM,
(4)在(3)的条件下,在x轴上找一点N,使MN+AN的值最小,求点N的坐标;
解:如答图2,作点A关于x轴的对称点A′,连接A′M,交x轴于点N,此时MN+AN的值最小.由对称的性质,得A′(1,-3).
(5)如图5,若点B关于直线y=x的对称点为点D,求过A,B,D三点的抛物线的解析式;
解:∵点B(-3,0)和点D关于直线y=x对称,∴D(0,-3).设该抛物线的解析式为y=ax2+bx+c.将A(1,3),B(-3,0),D(0,-3)代入y=ax2+bx+c,
(6)如图6,点P为x轴上一点,若△ABP是以AB为腰的等腰三角形,请直接写出点P的坐标.
解:点P的坐标为(5,0)或(-8,0)或(2,0).
②如答图4,当AB=PB时,5=|-3-a|.解得a=2或a=-8,即P2(2,0),P3(-8,0).
1.(2021广东)在平面直角坐标系xOy中,一次函数y=kx+b(k>0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数 y= 图象的一个交点为P(1,m).(1)求m的值;
若PA=2AB,可分为以下两种情况:①如答图5,当点B在y轴正半轴时(记为B1),b>0,此时点A在x轴负半轴(记为A1),过点P作PH⊥x轴于点H,则B1O∥PH.∴△A1B1O∽△A1PH.
(2)若PA=2AB,求k的值.
2.如图7,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于点A(-2,a),B(b,-1),过点A作AC⊥x轴于点C,已知S△AOC=4.
(2)结合图象直接写出关于x的不等式mx+n> 的解集;
解:x<-2或0<x<8.
(3)若点P是y轴上一动点,当|PB-PA|最大时,求点P的坐标.
解:如答图6,作点A关于y轴的对称点A′,连接A′B,延长BA′交y轴于点P,点P即为所求.由对称的性质,得A′(2,4).设直线A′B的解析式为y=cx+d.把点A′(2,4),B(8,-1)代入,
3.(原创)如图8,在平面直角坐标系中,一次函数y= x+5的图象与正比例函数y=-2x的图象交于点A,与x轴交于点B,与反比例函数y= 的图象交于点A,C,连接OC.
(1)求反比例函数的解析式.
(2)求△ACO的面积.
解:如答图7,过点A作AH⊥x轴于点H,过点C作CM⊥x轴于点M.
(3)在平面直角坐标系中是否存在一点P,使得以点A,B,O,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
类型 反比例函数与几何图形综合例2 (2020广东)如图9,点B是反比例函数y= (x>0)图象上一点,过点B分别向坐标轴作垂线,垂足为A,C.反比例函数y= (x>0)的图象经过OB的中点M,与AB,BC分别相交于点D,E.连接DE并延长交x轴于点F,点G与点O关于点C对称,连接BF,BG.(1)填空:k=________;
(2)求△BDF的面积;
(3)求证:四边形BDFG为平行四边形.
4.如图10,在△AOB中,∠ABO=90°,边OB在x轴上,反比例函数y= (x>0)的图象经过斜边OA的中点M,与AB相交于点N,已知S△AOB=12,AN= .(1)求k的值;
(2)求直线MN的解析式.
5.(2023泰州)在平面直角坐标系xOy中,点A(m,0),B(m-a,0)(a>m>0)的位置和函数 y1 = (x>0),y2= (x<0)的图象如图11所示.以AB为边在x轴上方作正方形ABCD,AD边与函数y1的图象相交于点E,CD边与函数y1,y2的图象分别相交于点G,H,一次函数y3的图象经过点E,G,与y轴相交于点P,连接PH.
(1)若m=2,a=4,求一次函数y3的表达式及△PGH的面积.
∴一次函数y3的表达式为y3=-2x+5.令x=0,得y3=5.∴P(0,5).∴OP=5.如答图12,设CD与y轴交于点M,则OM=BC=4.∴PM=OP-OM=5-4=1.
(2)当a,m在满足a>m>0的条件下任意变化时,△PGH的面积是否变化?请说明理由.
解:△PGH的面积不变.理由如下:
∴b1=a+1.∴P(0,a+1).∴OP=a+1.
(3)试判断直线PH与BC边的交点是否在函数y2的图象上?并说明理由.
解:直线PH与BC边的交点在函数y2的图象上.理由如下:如答图13,设直线PH与BC边的交点为点N.设直线PH的解析式为y=k2x+b2.
6.如图12,在平面直角坐标系中,矩形OABC的顶点A,C分别落在x轴、y轴的正半轴上,顶点B的坐标为(2,2 ),反比例函数y=(x>0)的图象与BC,AB边分别交于点D,E,连接AC,DE,已知BD= .
(1)求反比例函数的解析式和点E的坐标;
(2)判断DE与AC的位置关系,并说明理由;
(3)点F在直线AC上,点G是平面直角坐标系内一点,当四边 形BCFG为菱形时,求点G的坐标,并判断点G是否在反比例函数图 象上.
解:如答图14,当点F在点C的下方时,点G在点F的右方.过点F1作F1H⊥y轴于点H.∵四边形BCF1G1为菱形,∴BC=CF1=F1G1=BG1=2.
(1)求m的值和一次函数的表达式;
∵点A(1,4),C(0,3)在一次函数y=kx+b的图象上,把点A(1,4),C(0,3)代入y=kx+b,
∴一次函数的表达式为y=x+3.
解:在一次函数y=x+3中,令y=0,则x+3=0.解得x=-3.∴B(-3,0),即OB=3.∵C(0,3),∴OC=3.∵A(1,4),∴xA=1.
(1)求k,m的值;
解:∵OA=1,∴点A的坐标为(-1,0).把点A(-1,0)代入y=kx+2,得-k+2=0.解得k=2.∴直线l的解析式为y=2x+2.
∵点C在直线l上,点C的横坐标为2,∴在y=2x+2中,令x=2,则y=2×2+2=6.∴点C的坐标为(2,6).
(2)平行于y轴的动直线与l和反比例函数的图象分别交于点D,E,若以B,D,E,O为顶点的四边形为平行四边形,求点D的坐标.
∵OB∥DE, ∴当OB=DE时,以B,D,E,O为顶点的四边形为平行四边形.在y=2x+2中,令x=0,则y=2.∴点B的坐标为(0,2),即OB=2.
(1)分别求出一次函数和反比例函数的表达式;
解:∵四边形OABC为矩形,OA=2,OC=4.∴BC=OA=2,B(4,2).∵D是线段OB的中点,∴由中点坐标公式,得点D的坐标为(2,1).
(2)点P是x轴上一动点,当PE+PF的值最小时,点P的坐标为_________.
【提示】如答图1,作点E关于x轴的对称点E′,连接E′F交x轴于点P,此时PE+PF的值最小,点P即为所求.
(1)求m,n的值与点A的坐标;
解:将点P(-1,2)代入y=mx,得2=-m.解得m=-2.∴正比例函数的解析式为y=-2x.
由正比例函数与反比例函数图象的对称性,得点A,P关于原点对称.又P(-1,2),∴A(1,-2).
(2)求证:△CPD∽△AEO;
证明:∵四边形ABCD是菱形,∴AC⊥BD,AB∥CD.∴∠CPD=90°,∠DCP=∠OAE.∵AB⊥x轴,∴∠AEO=90°.∴∠CPD=∠AEO.∴△CPD∽△AEO.
中考数学二轮复习 专题突破课件 专题九 综合实践类: 这是一份中考数学二轮复习 专题突破课件 专题九 综合实践类,共60页。PPT课件主要包含了题型讲练,①②③,答图1,答图2,等腰三角形,等腰直角三角形,8×10-9,C12H26,强化训练,图2①等内容,欢迎下载使用。
中考数学二轮复习 专题突破课件 专题五 圆综合: 这是一份中考数学二轮复习 专题突破课件 专题五 圆综合,共60页。PPT课件主要包含了题型讲练,答图2,答图3,答图4,答图6,答图7,答图8,答图9,答图1,答图5等内容,欢迎下载使用。
中考数学复习重难突破小专题(二)反比例函数与几何综合课件: 这是一份中考数学复习重难突破小专题(二)反比例函数与几何综合课件,共15页。PPT课件主要包含了-20等内容,欢迎下载使用。












