






中考数学二轮专题复习课件 专题七 二次函数综合问题
展开二次函数综合问题是中考的必考题,一般与存在性问题、分类讨论问题等相结合,以多问解答的形式出现,第一问是对基础知识的考查,如求表达式等,第二问是对知识点的应用或小的拓展,第三问是在前两问的基础上进行的开放式探究,这类问题的知识覆盖面较广,综合性较强,题意构思非常精巧,解题方法灵活,对分析问题和解决问题的能力要求较高.
与线段、周长、面积等有关的综合题
此类问题主要有以下几种考查方式:①线段的和或差是定值;②线段定长;③求几条线段和或差的最值;④求周长或面积的最值.涉及知识点主要有两点之间,线段最短;垂线段最短;三角形的三边关系;“将军饮马”问题等.(1)平行于坐标轴的线段的最值问题,常通过利用线段两端点的坐标差表示出线段长的函数表达式,利用函数性质求解.确定函数最值时,函数自变量的取值范围应确定正确.
(2)已知一条定直线和直线同侧的两个定点,要求在定直线上确定一点,使得这个点到两定点距离和最小,其变形问题有三角形周长最小或四边形周长最小等.这类问题的解决方法是:作其中一个定点关于已知直线的对称点,连接对称点与另一个定点,所得直线与已知直线的交点即为所求的点,然后通过求直线的表达式及其与定直线的交点坐标,计算最小值或点的坐标.
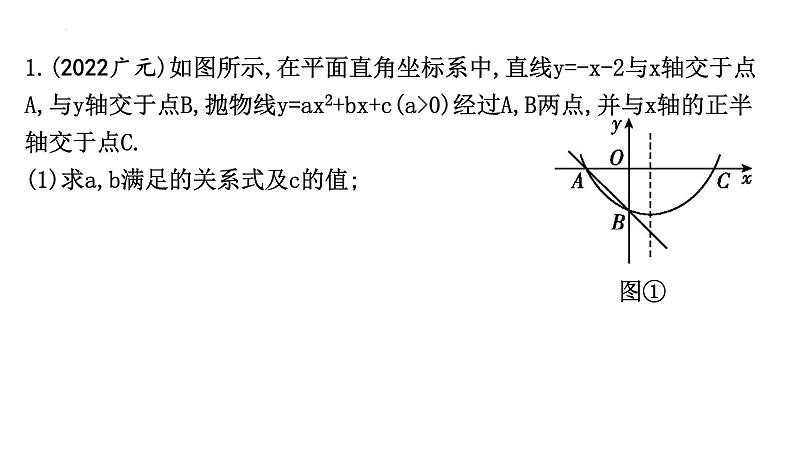
1.(2022广元)如图所示,在平面直角坐标系中,直线y=-x-2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a>0)经过A,B两点,并与x轴的正半轴交于点C.(1)求a,b满足的关系式及c的值;
(3)如图②所示,当a=1时,若点Q是直线AB下方抛物线上的一个动点,过点Q作QD⊥AB于点D,当QD的值最大时,求此时点Q的坐标及QD的最大值.
(1)特殊角问题常见破解策略:①运用三角函数值;②遇45°角构造等腰直角三角形;③遇30°,60°角构造等边三角形;④遇90°角构造直角三角形.(2)角的数量关系问题常见破解策略:①证等角:常运用等腰三角形两底角相等,等角的余(补)角相等,全等或相似三角形的对应角相等,两角的锐角三角函数值相等;②证二倍角:构造等腰三角形,利用顶角处的外角,或构造辅助圆,利用圆周角定理;③证和差角:旋转、翻折、平移构造角.
2.(2023淄川一模)已知抛物线y=-x2+(m2+3)x-(6m+9)(其中m≠0)与x轴交于点A,B,点B在点A的右侧,与y轴交于点C,其中点B的坐标为(3,0),如图所示.(1)求抛物线的函数表达式和抛物线的对称轴;
解:(1)把(3,0)代入y=-x2+(m2+3)x-(6m+9),化简整理,得m2-2m-3=0,∴m1=3,m2=-1.当m=3时,抛物线为y=-x2+12x-27,此时与x轴交点坐标分别为A(3,0),B(9,0),不符合B(3,0),∴m=3舍去;当m=-1时,抛物线为y=-x2+4x-3,此时与x轴的交点坐标分别为A(1,0),B(3,0),符合题意,∴抛物线的函数表达式为y=-x2+4x-3,对称轴是直线x=2.
(2)在抛物线的对称轴上找一点P,使PA+PC的值最小,请求出点P的坐标;
(3)Q为抛物线上一点,若∠ACQ=45°,求点Q的坐标.
3.如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于A(-2,0),B(8,0)两点,与y轴交于点C(0,4),连接AC,BC.(1)求抛物线的表达式;
(2)将△ABC沿AC所在直线翻折,得到△ADC,点B的对应点为D,直接写出点D的坐标,并求出四边形OADC的面积;
(3)点P是抛物线上的一动点,当∠PCB=∠ABC时,求点P的坐标.
探究特殊三角形的存在性问题
(1)二次函数与直角三角形存在性问题:①列出三角形三个顶点A,B,C的坐标,动点用参数表示;②用含参数的式子表示AB,AC,BC的长度(或平方);③分类列方程:①AB2+AC2=BC2,②AB2+BC2=AC2,③AC2+BC2=AB2;④解方程求出点的坐标,并检验是否符合题意,且能构成三角形.(2)二次函数与等腰三角形存在性问题:①列点:列出构建所求等腰三角形的三个点,定点找到后,动点用参数表示其坐标;②列线:用两点坐标表示其线段长度,列出三边长的平方;③列式:采用分类讨论思想,列出方程并求解、检验.
4.如图①所示,已知抛物线L:y=x2+bx+c经过点A(0,3),B(1,0),过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.(1)求抛物线的函数表达式.
(2)若动点P在直线OE下方的抛物线上,连接PE,PO,当△OPE面积最大时,求出点P坐标.
(3)将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围.
解:(3)由y=x2-4x+3=(x-2)2-1,得抛物线L的对称轴为直线x=2,顶点为(2,-1).抛物线L向上平移h个单位长度后顶点为H(2,-1+h).如图②所示,设直线x=2交OE于点M,交AE于点N.∵直线OE的表达式为y=x,∴M(2,2).∵点H在△OAE内(包括△OAE的边界),∴2≤-1+h≤3,解得3≤h≤4.
(4)如图②所示,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
5.(2022柳州)已知抛物线y=-x2+bx+c与x轴交于A(-1,0),B(m,0)两点,与y轴交于点C(0,5).(1)求b,c,m的值;
(2)如图①所示,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,垂足为点F,当四边形DEFG的周长最大时,求点D的坐标;
解:(2)∵抛物线的表达式为y=-x2+4x+5=-(x-2)2+9,∴对称轴为直线x=2,设D(x,-x2+4x+5).∵DE∥x轴,∴E(4-x,-x2+4x+5).∵过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,∴四边形DEFG是矩形,∴四边形DEFG的周长=2(-x2+4x+5)+2(x-4+x)=-2x2+12x+2=-2(x-3)2+20,∴当x=3时,四边形DEFG的周长最大,此时y=-32+4×3+5=8.∴当四边形DEFG的周长最大时,点D的坐标为(3,8).
(3)如图②所示,点M是抛物线的顶点,将△MBC沿BC翻折得到△NBC,NB与y轴交于点Q,在对称轴上找一点P,使得△PQB是以QB为直角边的直角三角形,求出所有符合条件的点P的坐标.
解:(3)如图所示,过点C作CH⊥对称轴于点H,过点N作NK⊥y轴于点K,∴∠NKC=∠MHC=90°.由翻折得CN=CM,∠BCN=∠BCM.∵B(5,0),C(0,5),∴OB=OC,∴∠OCB=∠OBC=45°.
∵CH⊥对称轴于点H,∴CH∥x轴,∴∠BCH=45°,∴∠BCH=∠OCB,∴∠NCK=∠MCH,∴△MCH≌△NCK(AAS),∴NK=MH,CK=CH.∵抛物线的表达式为y=-x2+4x+5=-(x-2)2+9,∴对称轴为直线x=2,M(2,9),∴MH=9-5=4,CH=2,∴NK=MH=4,CK=CH=2,∴N(-4,3).
探究特殊四边形的存在性问题
平行四边形的存在性问题:(1)①已知平行四边形的三个顶点,利用平行四边形对边平行且相等或对角线互相平分的性质可以确定第四个顶点.具体做法是:利用三点中任意两点的横、纵坐标之和减去第三点的横、纵坐标,得出第四点的横、纵坐标;再根据第四点满足的条件(在某个函数图象上)解方程即可.②已知平面内两个点A,B的坐标,求两点P,Q,使得A,B,P,Q四个点组成平行四边形(题目中点P,Q的位置一般有具体的限制),分两种情况讨论:一是若AB为平行四边形的边,将AB上下左右平移,确定点P,Q的位置;二是若AB为平行四边形的对角线,取AB中点,旋转经过中点的直线确定点P,Q的位置.求点的坐标时,可通过点的平移,构造全等三角形来求坐标.
该类问题常用“对点法”简捷求解:平行四边形的两组对角顶点的横、纵坐标的和分别相等.如图所示,由平行四边形的对边平行且相等,可知点B平移到点A与点C平移到点D的路径完全相同,故有xA-xB=xD-xC,yA-yB=yD-yC.故xA+xC=xD+xB,yA+yC=yD+yB.(2)矩形的存在性问题可转化为直角三角形的存在性问题来解决.(3)菱形的存在性问题可转化为等腰三角形的存在性问题来解决.(4)正方形的存在性问题可转化为等腰直角三角形的存在性问题来解决.
6.如图所示,二次函数y=ax2+bx+c的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为-1,点M(1,m)是其对称轴上一点,y轴上有一点B(0,1).(1)求二次函数的表达式.
(2)二次函数在第四象限的图象上有一点P,连接PA,PB,设点P的横坐标为t,△PAB的面积为S,求S与t的函数关系式.
(3)在二次函数图象上是否存在点N,使得以A,B,M,N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标;若不存在,请说明理由.
解:(3)存在.点N的坐标为(1,-1)或(3,3)或(-1,3).提示:设N(n,n2-2n),由A(2,0),B(0,1)及点M的横坐标为1,利用平移性质及“对点法”可知:当AB为对角线时,有2+0=1+n,∴n=1,∴N(1,-1);当AM为对角线时,有2+1=n+0,∴n=3,∴N(3,3);当AN为对角线时,有2+n=0+1,∴n=-1,∴N(-1,3).综上可知,点N的坐标为(1,-1)或(3,3)或(-1,3).
(2)D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时点D的坐标.
(3)若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
8.如图所示,某一次函数与二次函数y=x2+mx+n的图象交点为A(-1,0),B(4,5).(1)求抛物线的表达式;
(2)点C为抛物线对称轴上一动点,当AC与BC的和最小时,点C的坐标为 ; (3)点D为位于线段AB下方抛物线上一动点,过点D作DE⊥x轴,交线段AB于点E,求线段DE长度的最大值;
(4)在(2)的条件下,点M为y轴上一点,点F为直线AB上一点,点N为平面直角坐标系内一点,若以点C,M,F,N为顶点的四边形是正方形,请直接写出点N的坐标.
解:(4)当CF为对角线时,如图①所示.
此时四边形CMFN是正方形,∴N(1,1).
如图②所示,当CF为边时,当点F在点C的上方时,
此时∠MFC=45°,∴MF∥x轴.∵△MCF是等腰直角三角形,∴MF=CN=2,∴N(1,4).
当点F在点C的下方时,如图③所示,四边形CFNM是正方形,
同理可得N(-1,2).
当CM为对角线时,如图④所示,四边形CFMN是正方形,
探究全等或相似三角形的存在性问题
解答三角形相似的存在性问题时,要运用分类讨论的思想及数形结合的思想,具体方法步骤如下:(1)假设结论成立,分情况讨论.探究三角形相似时,往往没有明确指出两个三角形的对应角(尤其是以文字形式出现要证明两个三角形相似的题目),或者涉及动点问题,因动点问题中点的位置不确定,此时应考虑不同的对应关系,分情况讨论.(2)确定分类标准:在分类时,先要找出分类的标准,看两个相似三角形是否有对应相等的角.若有,找出对应相等的角后,再根据其他角进行分类讨论来确定相似三角形成立的条件;若没有,则分别按三对角对应来分类讨论.
(3)建立关系式,并计算.由相似三角形列出相应的比例式,将比例式中的线段用所设点的坐标表示出来(其长度多借助勾股定理计算),整理可得一元一次方程或者一元二次方程,解方程可得字母的值,再通过计算得出相应的点的坐标.
(2)点M是抛物线y1上一点,且位于x轴上方,横坐标为m,连接MC.若∠MCB=∠DAC,求m的值.
(3)如图②所示,将抛物线y1平移后得到顶点为B的抛物线y2.点P为抛物线y1上的一个动点,过点P作y轴的平行线,交抛物线y2于点Q,过点Q作x轴的平行线,交抛物线y2于点R.当以点P,Q,R为顶点的三角形与△ACD全等时,请直接写出点P的坐标.
10.(2023烟台一模)如图所示,抛物线y=ax2+bx+c经过点A(-2,0),点B(4,0),交y轴于点C(0,4).连接AC,BC.D为OB上的动点,过点D作ED⊥x轴,交抛物线于点E,交BC于点G.(1)求这条抛物线的表达式.
(2)过点E作EF⊥BC,垂足为点F,设点D的坐标为(m,0),请用含m的代数式表示线段EF的长,并求出当m为何值时EF有最大值,最大值是多少.
中考数学二轮复习 专题突破课件 专题七 反比例函数综合: 这是一份中考数学二轮复习 专题突破课件 专题七 反比例函数综合,共60页。PPT课件主要包含了-2x0或x1,题型讲练,解x1,答图1,分两种情况讨论,答图5,1求a和b的值,答图7,图10,图11等内容,欢迎下载使用。
中考数学二轮专题复习课件 专题三 二次函数综合: 这是一份中考数学二轮专题复习课件 专题三 二次函数综合,共54页。
中考数学二轮复习 专题突破 课件 二次函数综合(二): 这是一份中考数学二轮复习 专题突破 课件 二次函数综合(二),共60页。PPT课件主要包含了题型讲练,S△ACG,答图2,答图3,答图4,答图5,答图6,答图7,答图1,强化训练等内容,欢迎下载使用。












