中考数学二轮专题复习课件 专题五　圆的综合题

这是一份中考数学二轮专题复习课件 专题五　圆的综合题，共30页。PPT课件主要包含了圆与全等三角形的综合，圆与相似三角形的综合，圆与特殊三角形的综合，圆与特殊四边形的综合，与圆有关的动态综合题等内容，欢迎下载使用。

圆的综合题是中考数学的热门考题与重要内容,主要考查圆的切线的判定与性质,常与全等三角形、相似三角形、锐角三角函数、特殊三角形或四边形等知识相融合,证直线与圆的位置关系与乘积式,证线段或角相等,求线段长或角度大小,计算阴影面积等,凸显了数学的化归思想与逻辑推理,为几何图形的证明与计算提供了良好的载体.
1.如图所示,AB为☉O的直径,过圆上一点D作☉O的切线CD交BA的延长线于点C,过点O作OE∥AD交CD于点E,连接BE.(1)直线BE与☉O相切吗?请说明理由.
解:(1)直线BE与☉O相切.理由如下:连接OD,如图所示.∵CD与☉O相切于点D,∴∠ODE=90°.∵AD∥OE,∴∠ADO=∠DOE,∠DAO=∠EOB.∵OD=OA,∴∠ADO=∠DAO,∴∠DOE=∠EOB.又∵OD=OB,OE=OE,∴△DOE≌△BOE(SAS),∴∠OBE=∠ODE=90°.∵OB是☉O的半径,∴直线BE与☉O相切.
(2)若CA=2,CD=4,求DE的长.
解:(2)设☉O的半径为r.在Rt△ODC中,OD2+DC2=OC2,∴r2+42=(r+2)2,∴r=3,∴AB=2r=6,∴BC=AC+AB=2+6=8.由(1)得△DOE≌△BOE,∴DE=BE.在Rt△BCE中,BC2+BE2=CE2,∴82+BE2=(4+DE)2,∴64+DE2=(4+DE)2,解得DE=6,∴DE的长为6.
2.(2023威海)已知:射线OP平分∠MON,A为OP上一点,☉A交射线OM于点B,C,交射线ON于点D,E,连接AB,AC,AD.(1)如图①所示,若AD∥OM,试判断四边形OBAD的形状,并说明理由.
(1)解:四边形OBAD是菱形.理由如下:过点A作AF⊥ON于点F,AG⊥OM于点G,如图①所示.∵OP平分∠MON,AF⊥ON,AG⊥OM,∴AF=AG.又∵AD=AB,∴Rt△AFD≌Rt△AGB(HL),∴FD=GB.
∵OA=OA,AF=AG,∴Rt△AFO≌Rt△AGO(HL),∴OF=OG,∴OF-FD=OG-GB,即OD=OB.∵OP平分∠MON,∴∠AOD=∠AOB.∵AD∥OM,∴∠AOB=∠OAD,∴∠AOD=∠OAD,∴OD=AD,∴OD=AD=AB=OB,∴四边形OBAD是菱形.
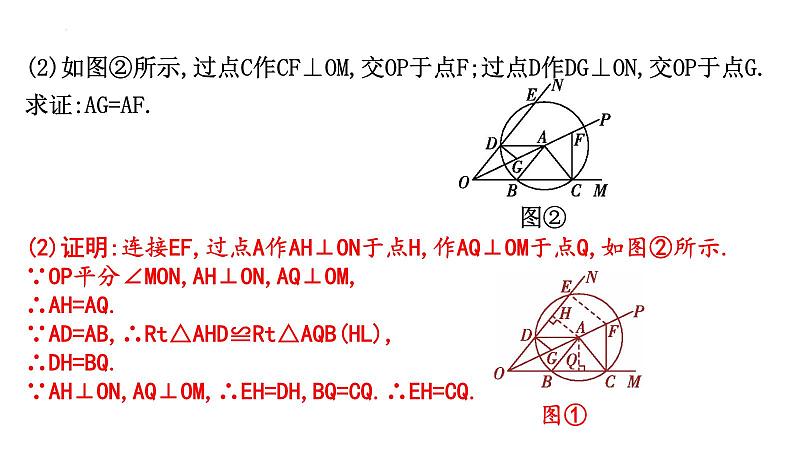
(2)如图②所示,过点C作CF⊥OM,交OP于点F;过点D作DG⊥ON,交OP于点G.求证:AG=AF.
(2)证明:连接EF,过点A作AH⊥ON于点H,作AQ⊥OM于点Q,如图②所示.∵OP平分∠MON,AH⊥ON,AQ⊥OM,∴AH=AQ.∵AD=AB,∴Rt△AHD≌Rt△AQB(HL),∴DH=BQ.∵AH⊥ON,AQ⊥OM,∴EH=DH,BQ=CQ.∴EH=CQ.
∵OA=OA,AH=AQ,∴Rt△AHO≌Rt△AQO(HL),∴OH=OQ,∴OH+EH=OQ+CQ,即OE=OC.又∵∠EOF=∠COF,OF=OF,∴△OEF≌△OCF(SAS),∴∠OEF=∠OCF=90°,∴EF⊥ON.∵DG⊥ON,AH⊥ON,∴DG∥AH∥EF.∵DH=EH,∴AG=AF.
3.(2022滨州)如图所示,已知AC为☉O的直径,直线PA与☉O相切于点A,直线PD经过☉O上的点B且∠CBD=∠CAB,连接OP交AB于点M.求证:(1)PD是☉O的切线;
证明:(1)如图所示,连接OB.∵AC是☉O的直径,∴∠ABC=90°,∴∠CAB+∠OCB=90°.∵OB=OC,∴∠OCB=∠OBC.又∵∠CBD=∠CAB,∴∠CBD+∠OBC=90°,即∠OBD=90°.又∵OB是☉O的半径,∴PD是☉O的切线.
(2)AM2=OM·PM.
4.(2023陕西)如图所示,△ABC内接于☉O,∠BAC=45°,过点B作BC的垂线,交☉O于点D,并与CA的延长线交于点E,作BF⊥AC,垂足为M,交☉O于点F.(1)求证:BD=BC;
(1)证明:如图所示,连接DC,则∠BDC=∠BAC=45°.∵BD⊥BC,∴∠BCD=90°-∠BDC=45°,∴∠BCD=∠BDC,∴BD=BC.
(2)若☉O的半径r=3,BE=6,求线段BF的长.
圆与锐角三角函数的综合
5.如图所示,在△ABC中,以AB为直径作☉O分别交AC,BC于点D,E,且D是AC的中点,过点D作DG⊥BC于点G,交BA的延长线于点H.(1)求证:直线HG是☉O的切线;
(1)证明:连接OD,如图所示.∵AD=DC,AO=OB,∴OD是△ABC的中位线,∴OD∥BC.∵DG⊥BC,∴OD⊥HG.又∵OD是☉O的半径,∴直线HG是☉O的切线.
(3)在(2)的条件下,当CP是∠ACB的平分线时,求CP的长.
8.(2023临沂)如图所示,☉O是△ABC的外接圆,BD是☉O的直径,AB=AC,AE∥BC,E为BD的延长线与AE的交点.(1)求证:AE是☉O的切线;
9.(2023东营一模)如图所示,在Rt△ABC中,∠ACB=90°,O是BC边上一点,以O为圆心,OB为半径的圆与AB相交于点D,连接CD,且CD=AC.(1)求证:CD是☉O的切线;
(2)如果AB=10,BF=6,求矩形ABCD的面积.
11.(2023烟台)如图所示,在菱形ABCD中,对角线AC,BD相交于点E,☉O经过A,D两点,交对角线AC于点F,连接OF交AD于点G,且AG=GD.(1)求证:AB是☉O的切线;
(1)证明:如图所示,连接OA,则OF=OA,∴∠OAF=∠OFA.∵AG=GD,∴OF⊥AD,∴∠AGF=90°.∵四边形ABCD是菱形,∴AB=AD,AC⊥BD,∴∠BAE=∠DAE,∴∠OAB=∠OAF+∠BAE=∠OFA+∠DAE=90°.∵OA是☉O的半径,∴AB是☉O的切线.
(2)已知☉O的半径与菱形的边长之比为5∶8,求tan∠ADB的值.
12.(2023娄底)如图①所示,点G为等边三角形ABC的重心,点D为BC边的中点,连接GD并延长至点O,使得DO=DG,连接GB,GC,OB,OC.(1)求证:四边形BOCG为菱形.
(1)证明:∵△ABC是等边三角形,G是重心,点D为BC边的中点,∴点A,G,D,O在BC的垂直平分线上,∴GO⊥BC,BD=DC.∵DO=DG,∴GO与BC互相垂直且平分,∴四边形BOCG是菱形.
(2)如图②所示,以O点为圆心,OG为半径作☉O.①判断直线AB与☉O的位置关系,并予以证明.
(2)①解:直线AB与☉O的位置关系是相切.证明:∵在等边三角形ABC中,∠ABC=60°,G是重心,∴∠ABG=∠GBC=30°.∵四边形BOCG是菱形,∴∠CBO=∠GBC=30°.∵∠ABO=∠ABG+∠GBC+∠CBO=90°,∴AB⊥OB.又∵OB为☉O的半径,∴AB与☉O相切.