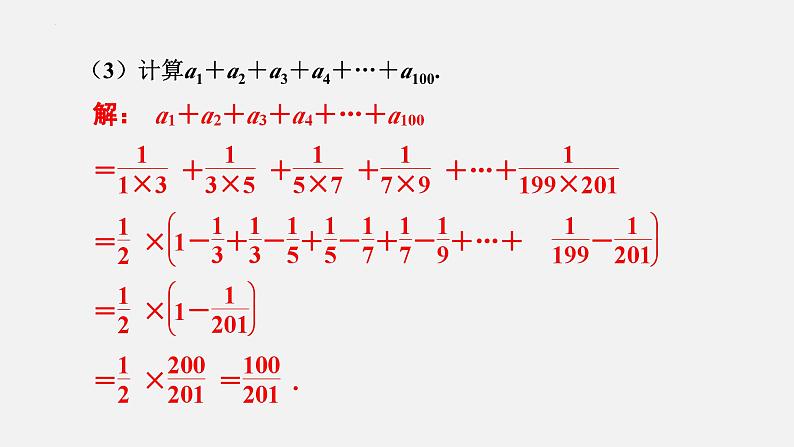
中考数学二轮复习专题突破课件 专题一　规律探究

这是一份中考数学二轮复习专题突破课件 专题一　规律探究，共29页。PPT课件主要包含了题型讲练，n＋6，n＋1－2，强化训练，n2－n等内容，欢迎下载使用。

类型 数式类规律例1　观察下列等式：
请解答下列问题：（1）按以上规律列出第5个等式：a5＝_______________________；（2）用含有n的代数式表示第n个等式：an＝_____________________＝____________________（n为正整数）；
（3）计算a1＋a2＋a3＋a4＋…＋a100.
1. 按一定规律排列的单项式：x2，2x4，4x6，8x8，16x10，32x12，…，则第n个单项式是（　　）A．2nx2n B．2n－1x2n C．（2n－2）x2n D．n2x2n
2．（2023恩施州）观察下列两行数，探究第②行数与第①行数的关系：－2，4，－8，16，－32，64，…①　0，7，－4，21，－26，71，…②根据你的发现，完成填空：第①行数的第10个数为________；取每行数的第2 023个数，则这两个数的和为________________．
－22 024＋2 024
3．将从1开始的连续自然数按以下规律排列：若有序数对（n，m）表示第n行，从左到右第m个数，如（3，2）表示6，则表示99的有序数对是___________．
4．（2023嘉兴）观察下面的等式：32－12＝8×1，52－32＝8×2， 72－52＝8×3，92－72＝8×4，…（1）写出192－172的结果；（2）按上面的规律归纳出一个一般的结论；（用含n的等式表示，n为正整数）解：（1）192－172＝8×9＝72.（2）（2n＋1）2－（2n－1）2＝8n.
（3）请运用有关知识，推理说明这个结论是正确的．解：∵（2n＋1）2－（2n－1）2 ＝[（2n＋1）＋（2n－1）][（2n＋1）－（2n－1）] ＝（2n＋1＋2n－1）（2n＋1－2n＋1） ＝4n×2 ＝8n，∴（2n＋1）2－（2n－1）2＝8n正确．
类型 图形类规律例2　（2023十堰）用火柴棍拼成如图1所示的图案，其中第①个图案由4个小等边三角形围成1个小菱形，第②个图案由6个小等边三角形围成2个小菱形……若按此规律拼下去，则第n个图案需要火柴棍的根数为________．（用含n的式子表示）图1
5.如图2，用相同的圆点按照一定的规律拼出图形，其中第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按此规律，第一百幅图中圆点的个数是（　　）图2A．297 B．301 C．303 D．400
6．如图3，在等腰直角三角形ABC中，∠ACB＝90°，AC＝BC＝1，AC边在直线l上，将△ABC绕点A顺时针旋转到位置①可得到点P1（点P1在直线l上），此时AP1＝ ；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2（点P2在直线l上），此时AP2＝1＋ ；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3（点P3在直线l上），此时AP3＝2＋ ……按此规律进行下去，则AP8＝____________．图3
7．如图4，已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1的各边延长一倍得到正方形A2B2C2D2；以此进行下去……则正方形A4B4C4D4的面积为________．图4
类型 坐标类规律例3　如图5，在平面直角坐标系中，A（－2，0），A1（0，2），点A，A1，A2，A3，…在直线l上，点B1，B2，B3，…在x轴的正半轴上，若△A1OB1，△A2B1B2，△A3B2B3，…依次均为等腰直角三角形，且直角顶点都在x轴上，则第n个等腰直角三角形AnBn－1Bn顶点Bn的横坐标为____________．图5
8.（2023泰安）已知△OA1A2，△A3A4A5，△A6A7A8，…都是边长为2的等边三角形，按如图6所示摆放．点A2，A3，A5，…都在x轴正半轴上，且A2A3＝A5A6＝A8A9＝…＝1，则点A2 023的坐标是_______________．图6
9．如图7，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O重合，AB∥x轴，交y轴于点P.将△OAP绕点O顺时针旋转，每次旋转90°，则第2 024次旋转结束时，点A的坐标为（　　）
10．如图8，已知等边三角形OA1B1，顶点A1在双曲线y＝ （x＞0）上，点B1的坐标为（2，0）.过B1作B1A2∥OA1交双曲线于点A2，过A2作A2B2∥A1B1交x轴于点B2，得到第二个等边三角形B1A2B2；过B2作B2A3∥B1A2交双曲线于点A3，过A3作A3B3∥A2B2交x轴于点B3，得到第三个等边三角形B2A3B3；以此类推……则点B6的坐标为______________．图8
2．将字母“C”，“H”按照如图1所示的规律摆放，依此规律，则第④个图形中字母“H”的个数是(　　)A．9 B．10 C．11 D．12
3．(2023牡丹江)观察下面两行数：1，5，11，19，29，…；1，3，6，10，15，….取每行数的第7个数，计算这两个数的和是(　　)A．92 B．87 C．83 D．78
4．如图2，在平面直角坐标系中，半径均为1个单位长度的半圆O1，O2，O3，…组成一条平滑的曲线，将一枚棋子放在原点O.第一步，棋子从点O跳到点A1(1，1)；第二步，从点A1跳到点A2(2，0)；第三步，从点A2跳到点A3(3，－1)；按此规律依次在曲线上向右跳动一步，则棋子跳到点A2 023时的坐标为(　　)A．(2 022，0) B．(2 023，1) C．(2 023，0) D．(2 023，－1)
5．(2023岳阳)观察下列式子：12－1＝1×0；22－2＝2×1；32－3＝3×2；42－4＝4×3；52－5＝5×4；…依此规律，则第n(n为正整数)个等式是____________________．
n2－n＝n(n－1)
6．如图3，用火柴棒按如下方式拼成一排由三角形组成的图形．若拼成的第n个图形恰好用了2 023根火柴棒，则n＝________．
7．如图4，已知矩形ABCD的长和宽分别为a，b，进行如下操作：第一次，顺次连接矩形ABCD各边的中点，得到四边形A1B1C1D1；第二次，顺次连接四边形A1B1C1D1各边的中点，得到四边形A2B2C2D2；如此反复操作下去，……，则第n次操作后，得到四边形AnBnCnDn的面积是__________．
8．如图5，在平面直角坐标系中，点A1的坐标为(1，0)，以OA1为直角边作Rt△OA1A2，使∠A1OA2＝60°；再以OA2为直角边作Rt△OA2A3，使∠A2OA3＝60°；再以OA3为直角边作Rt△OA3A4，使∠A3OA4＝60°；按此规律进行下去，……，则点A6的坐标为______________．
9．(2023绥化)在求1＋2＋3＋…＋100的值时，发现：1＋100＝101，2＋99＝101，…，从而得到1＋2＋3＋…＋100＝101×50＝5 050，按此方法可解决下面问题．如图6，图(1)有1个三角形，记作a1＝1；分别连接这个三角形三边中点得到图(2)，有5个三角形，记作a2＝5；再分别连接图(2)中间的小三角形三边中点得到图(3)，有9个三角形，记作a3＝9；按此方法继续下去，则a1＋a2＋a3＋…＋an＝________．(结果用含n的代数式表示)
10．阅读材料：求1＋2＋22＋23＋24＋…＋22 022的值．解：设S＝1＋2＋22＋23＋24＋…＋22 022，将等式两边同时乘2，得2S＝2＋22＋23＋24＋…＋22 022＋22 023.下式减去上式，得2S－S＝22 023－1，即S＝22 023－1.所以1＋2＋22＋23＋24＋…＋22 022＝22 023－1.请你仿照此法计算：
(1)1＋2＋22＋23＋24＋…＋210；
解：设S＝1＋2＋22＋23＋24＋…＋210.将等式两边同时乘2，得2S＝2＋22＋23＋24＋…＋211.下式减去上式，得S＝211－1.所以1＋2＋22＋23＋24＋…＋210＝211－1.