中考数学二轮复习 专题突破课件 二次函数综合（一）

这是一份中考数学二轮复习 专题突破课件 二次函数综合（一），共60页。PPT课件主要包含了－10，题型讲练，答图3，∠DBC＝2∠A，∠AOC＝2∠B，∠BAC＝2∠BAD，答图1，答图2，答图4，答图5等内容，欢迎下载使用。
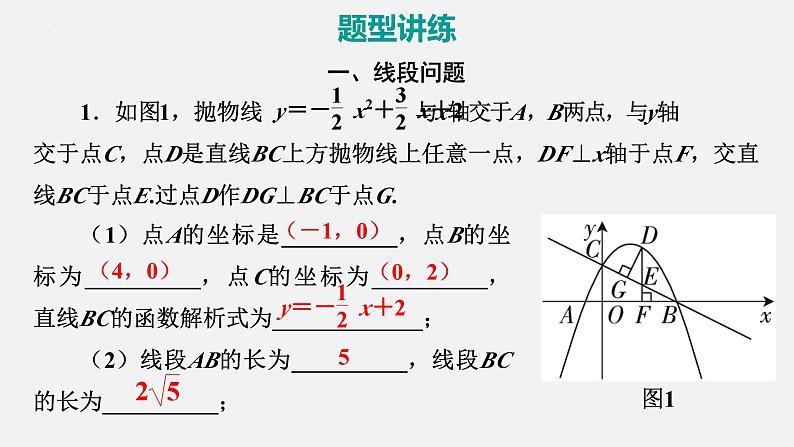
一、线段问题1．如图1，抛物线 与x轴交于A，B两点，与y轴交于点C，点D是直线BC上方抛物线上任意一点，DF⊥x轴于点F，交直线BC于点E.过点D作DG⊥BC于点G.
（1）点A的坐标是__________，点B的坐标为__________，点C的坐标为__________，直线BC的函数解析式为_____________；（2）线段AB的长为__________，线段BC的长为__________；
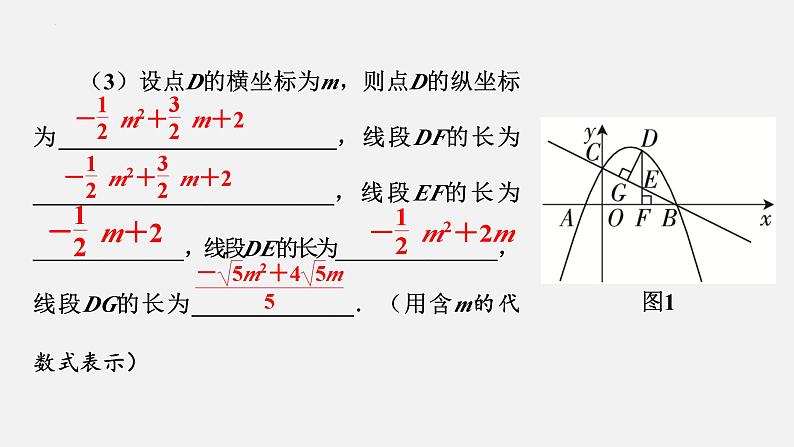
（3）设点D的横坐标为m，则点D的纵坐标为________________________，线段DF的长为__________________________，线段EF的长为_____________，线段DE的长为______________，线段DG的长为______________．（用含m的代数式表示）
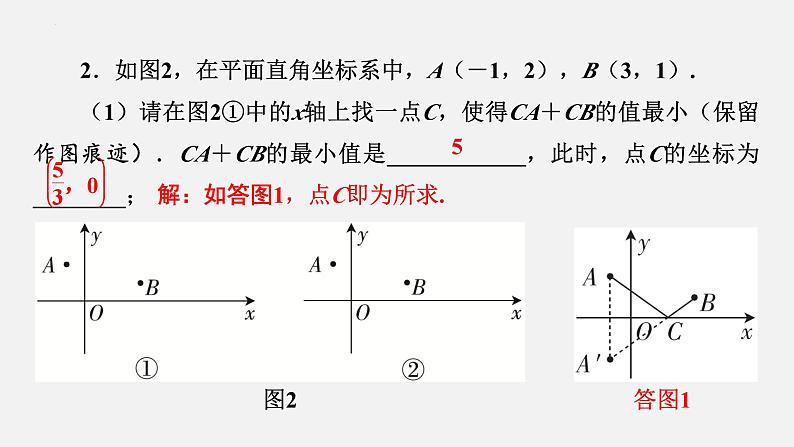
2．如图2，在平面直角坐标系中，A（－1，2），B（3，1）.（1）请在图2①中的x轴上找一点C，使得CA＋CB的值最小（保留作图痕迹）．CA＋CB的最小值是____________，此时，点C的坐标为________；
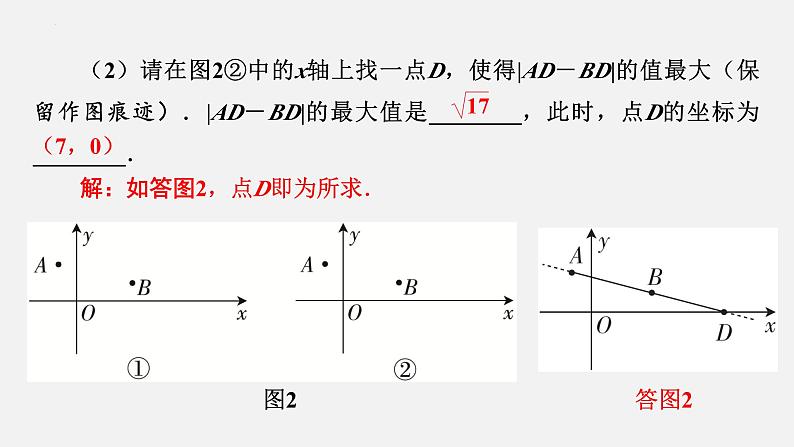
（2）请在图2②中的x轴上找一点D，使得|AD－BD|的值最大（保留作图痕迹）．|AD－BD|的最大值是________，此时，点D的坐标为________．
例1　已知抛物线y＝x2＋2x－3与x轴交于A，B两点（点B在点A的左侧），与y轴交于点C，连接BC，点P是抛物线上一点，过点P作PQ⊥x轴于点Q，交直线BC于点R.设点P的横坐标为m.
（1）如图3，当点P在直线BC下方时，请解答下列与线段PQ，QR，RP 相关的问题：
①点的坐标问题：请求出点P，R，Q的坐标；（用含m的代数式表示）
解：∵点P的横坐标为m，PQ⊥x轴于点Q，∴P（m，m2＋2m－3），Q（m，0）.把x＝0代入y＝x2＋2x－3，得y＝－3.∴C（0，－3）.把y＝0代入y＝x2＋2x－3，得x2＋2x－3＝0.解得x1＝－3，x2＝1.∴B（－3，0）.
②线段的表示问题：请用含m的代数式表示线段PR，QR的长度；
解：由（1）①，得P（m，m2＋2m－3），Q（m，0）， R（m，－m－3），∴PR＝（－m－3）－（m2＋2m－3）＝－m2－3m，QR＝0－（－m－3）＝m＋3.
③线段长度是定值问题：若PR＝2，求点P的坐标；
解：由（1）②，得PR＝－m2－3m.当PR＝2时，－m2－3m＝2.解得m1＝－2，m2＝－1.∴P1（－2，－3），P2（－1，－4）.
④线段数量关系问题：若PR＝QR，求点P的坐标；
解：由（1）②，得PR＝－m2－3m，QR＝m＋3.∵PR＝QR，∴－m2－3m＝m＋3.解得m3＝－3（不合题意，舍去），m4＝－1.∴P（－1，－4）.
⑤线段长度最值问题：当线段PR长度取得最大值时，求点P的坐标．
（2）当P，Q，R三个点中的一个点为另外两点所连线段的中点时，求m的值．
解：ⅰ.当Q为PR的中点时，yP＋yR＝2yQ.即m2＋2m－3＋（－m－3）＝0.解得m5＝－3（舍去），m6＝2.ⅱ.当R为PQ的中点时，yP＋yQ＝2yR.即m2＋2m－3＋0＝2（－m－3）.解得m7＝－3（舍去），m8＝－1.
（3）如图4，若点P在直线BC下方，过点P作PM⊥BC于点M.①当PM的值最大时，求点P的坐标；
解：易得－3＜m＜0.由（1），得当－3＜m＜0时，PR＝－m2－3m.在Rt△BOC中，OB＝OC＝3，∴∠OBC＝45°.∴∠QRB＝45°.∴∠PRM＝∠QRB＝45°.∵PM⊥BC，∴∠PMR＝90°.
②求△PRM的周长的最大值，并求出此时点P的坐标．
　 1.如图5，在平面直角坐标系中，已知抛物线y＝ax2＋bx＋c与x轴交于点A（－3，0），B（1，0）两点，与y轴交于点C（0，3），点P是抛物线上的一个动点．（1）求抛物线的解析式；
（2）当点P在直线AC上方时，连接BP交AC于点D，求 的最大值及此时点P的坐标．
2．如图6①，抛物线y＝－x2＋bx＋c经过A（－1，0），C（0，3）两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与y轴交于 点D.
（1）求该抛物线的解析式；
（2）若点H是x轴上一动点，连接MH，DH，求MH＋DH的最小值；
（3）如图6②，点P是直线AM上方抛物线上一动点，过点P作x轴的平行线交直线AM于点E，过点P作y轴的平行线交x轴于点F，求PE＋PF的最大值及此时点P的坐标．
二、角度问题1．（原创）如图1，A（－1，0），B（3，0），C（0，－3）.点P是直线x＝2上一点．（1）若∠PAB＝30°，则点P的坐标是_______________________；
（2）若∠PAB＝60°，则点P的坐标是________________________；（3）若∠PAB＝45°，则点P的坐标是_______________________；（4）若∠PCB＝15°，则点P的坐标是________________________________________．
（2，3）或（2，－3）
2．（1）如图2，AB＝BC，延长AB到点D，连接DC，则∠DBC与∠A的数量关系是_______________；（2）如图3，在⊙O中，∠AOC与∠B的数量关系是_____________；（3）如图4，AD所在的直线是△ABC的对称轴，则∠BAC与∠BAD的数量关系是_________________． 图2 图3 图4
例1　如图5，抛物线y＝x2＋2x－3与x轴交于A，B两点（点B在点A左侧），与y轴交于点C，连接AC，BC.点P是抛物线上一动点．（1）若∠PAB＝∠ACO，求点P的坐标；
解：把y＝0代入y＝x2＋2x－3，得x2＋2x－3＝0.解得x1＝1，x2＝－3.∴B（－3，0），A（1，0）.把x＝0代入y＝x2＋2x－3，得y＝－3.∴C（0，－3）.∴OA＝1，OC＝3.
（2）若点P是位于第二象限的抛物线上一点，且满足∠PCB＝∠ACO，求点P的坐标；
（3）若点P是位于第二象限的抛物线上一点，且满足∠PAB＝2∠ACO，求点P的坐标．
例2　如图6，抛物线y＝x2－2x－3与x轴交于点A，B（点A在点B左侧），与y轴负半轴交于点C，连接AC，点P是抛物线上一点．（1）若直线CP交x轴负半轴于点D且∠ACD＝45°，求点P的坐标；
把y＝0代入y＝x2－2x－3，得x2－2x－3＝0.解得x1＝－1，x2＝3.∴A（－1，0），B（3，0）.∴OA＝1.把x＝0代入y＝x2－2x－3，得y＝－3.∴C（0，－3）.∴OC＝3.∵AE⊥AC，∠ACD＝45°，∴∠FAE＋∠OAC＝90°，△ACE为等腰直角三角形．∴AC＝AE.
又EF⊥x轴，∴∠FEA＋∠FAE＝90°，∠EFA＝∠AOC＝90°.∴∠FEA＋∠FAE＝∠FAE＋∠OAC.∴∠FEA＝∠OAC.
（2）若直线CP交x轴于点D且∠ACD＝45°，求点P的坐标；
②当点D在点A的右侧时，如答图4，过A作AM⊥AC交CP于点M，过M作MN⊥x轴于点N.当∠ACP＝45°时，同（1）可证△AMN≌△CAO.∴MN＝AO＝1，AN＝CO＝3.∴ON＝AN－AO＝2.∴M（2，1）.
（3）如图7，若动点P满足∠OBP的度数不大于30°，求点P的横坐标的取值范围；
（4）如图8，连接BC，若动点P满足∠BCP＝15°，求点P的坐标．
解：由（1），得OC＝OB＝3.∴∠OCB＝∠OBC＝45°.
设P（a，a2－2a－3）.如答图6，当∠PCB＝15°时，分两种情况讨论：
①当点P1在x轴上方时，过点P1作P1H1⊥y轴于点H1，则∠P1CH1＝∠BCO－∠P1CB＝30°.
　 1.（原创）如图9，抛物线y＝－ x2＋x＋4与x轴交于 A（－2，0），B（4，0）两点，与y轴交于点C（0，4），点D是抛物线的顶点，点C关于抛物线的对称轴对称的点为C1.
（1）抛物线的顶点D的坐标为__________，点C1的坐标为__________．（2）若点P为y轴负半轴上一点，满足∠BCO＝∠APO，则点P的坐标为___________．（3）若点P为抛物线对称轴上的一点，满足∠ACO＝∠BPD，则 点P的坐标为______________________.　
（1，－6）或（1，6）
（4）若点P为x轴上的一点，满足∠ACO＝∠CPO，则点P的坐标为____________________．（5）若点P为抛物线上的一点，点P的横坐标为m，则点P到x轴的距离为________________；点P到y轴的距离为_________；点P到直线CC1的距离为__________________．（用含m的式子表示）
（－8，0）或（8，0）
（6）若点P为位于直线CC1下方的抛物线上一点，且满足∠ACO＝∠PCC1，则点P的坐标为________.　
（7）若点P为位于x轴下方的抛物线上一点，且满足∠PAB＝∠CBC1，则点P的坐标为________________．
（8）若点P为抛物线对称轴上一点，满足∠PAC1＝∠PC1A，则点P的坐标为__________．（9）若点P为抛物线上的一点，满足∠PC1O＝∠C1OB，则点P的坐标为___________________．
一、线段问题1.如图1，抛物线y＝－x2＋bx＋c与x轴交于A(1，0)，B(－3，0)两点．(1)求该抛物线的函数解析式．
解：将A(1，0)，B(－3，0)分别代入y＝－x2＋bx＋c，
(2)设该抛物线交y轴于点C，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出点Q的坐标；若不存在，请说明理由.
解：存在点Q，使得△QAC的周长最小．如答图1，连接BC，与对称轴交于点Q.此时QB＋QC的值最小．∵A，B两点关于抛物线的对称轴对称，∴QA＝QB.∴QB＋QC的值最小时，QA＋QC的值最小，即△QAC的周长最小．
在y＝－x2－2x＋3中，当x＝0时，y＝3.∴点C的坐标是(0，3).设直线BC的解析式为y＝kx＋t.
2．如图2，已知抛物线y＝ax2＋bx－3与x轴交于A(－2，0)，B(6，0)两点，与y轴交于点C.(1)求该抛物线的函数解析式；
解：如答图2，过点A作AE∥y轴交BC于点E，过点P作PF∥y轴交BC于点F.∴PF∥AE.
1．综合与探究：如图1，抛物线y＝－ x2＋x＋4与x轴交于A，B两点(点A在点B的左侧)，与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴交x轴于点E，点P是位于第一象限内且在对称轴右侧抛物线上的一个动点,设点P的横坐标为m，点F的坐标为(0，－3)，连接FP，FP分别与x轴、抛物线的对称轴交于点G，H. 
(1)求A，B，C三点的坐标并直接写出顶点D的坐标．
(2)试探究:在点P运动过程中,是否存在点P,使得∠FHE＝135°？若存在，请直接写出m的值；若不存在，请说明理由．
【提示】由∠FHE＝135°可得△OFG是等腰直角三角形．∴OG＝OF＝3，即G(3，0).∴直线FG的解析式为y＝x－3.
(1)求抛物线的函数解析式．
(2)在直线BC上方的抛物线上是否存在一点D，使得∠DCB＝2∠ABC？若存在，求出点D的坐标；若没有，请说明理由．
解：存在．如答图1，作点B关于y轴的对称点B′，作射线B′C交抛物线于点D.
解得x＝－1或x＝4.∴B(4，0).∴B′(－4，0).设直线B′C的解析式为y＝kx＋t.把B′(－4，0)，C(0，3)代入，