山东省日照市东港区日照港中学2023-2024学年八年级下学期3月月考数学试题（原卷版+解析版）

这是一份山东省日照市东港区日照港中学2023-2024学年八年级下学期3月月考数学试题（原卷版+解析版），文件包含山东省日照市东港区日照港中学2023-2024学年八年级下学期3月月考数学试题原卷版docx、山东省日照市东港区日照港中学2023-2024学年八年级下学期3月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。

一、单选题（每小题3分，满分30分）
1. 若代数式有意义，则实数x的取值范围是（ ）
A. B. 且C. D. 且
2. 下列各式计算正确的是（ ）
A. B. C. D.
3. 下列条件中，不能判定是直角三角形的是（ ）
A. B.
C. D.
4. 下列根式中，能与合并的二次根式是（ ）
A B. C. D.
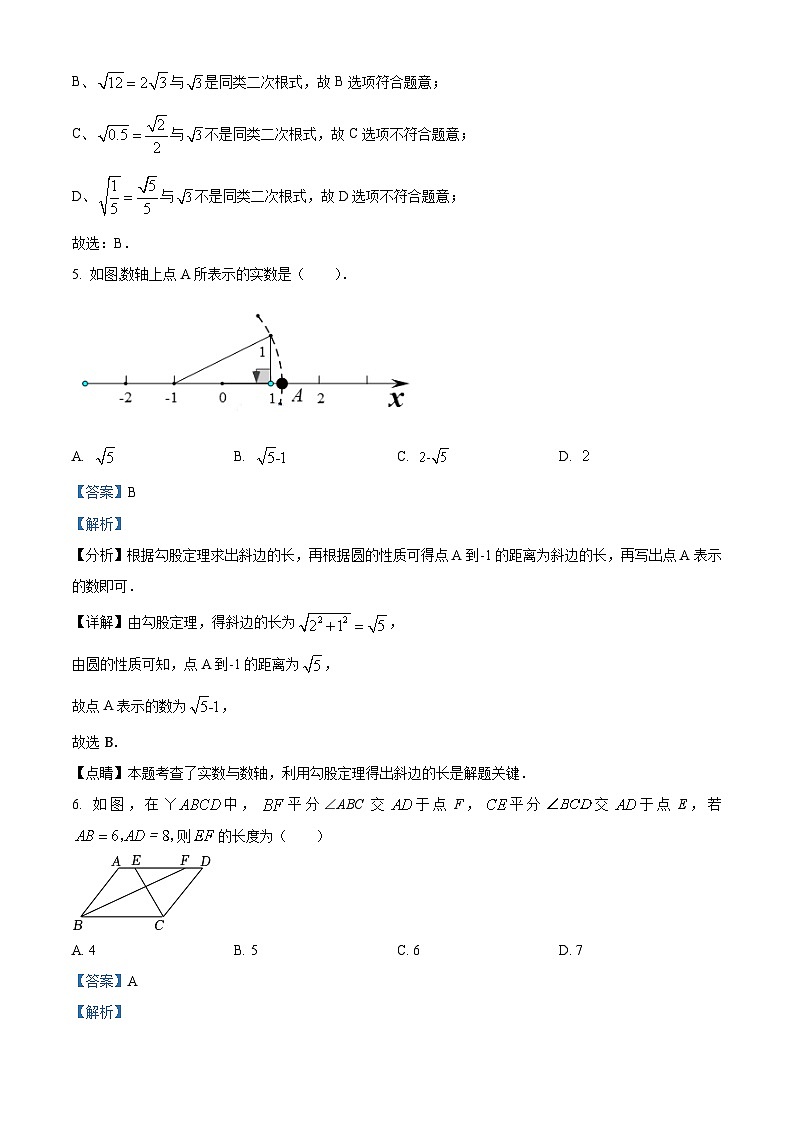
5. 如图,数轴上点A所表示的实数是（ ）．
A. B. C. D.
6. 如图，在中，平分∠ABC交于点F，平分交于点E，若则的长度为（ ）
A. 4B. 5C. 6D. 7
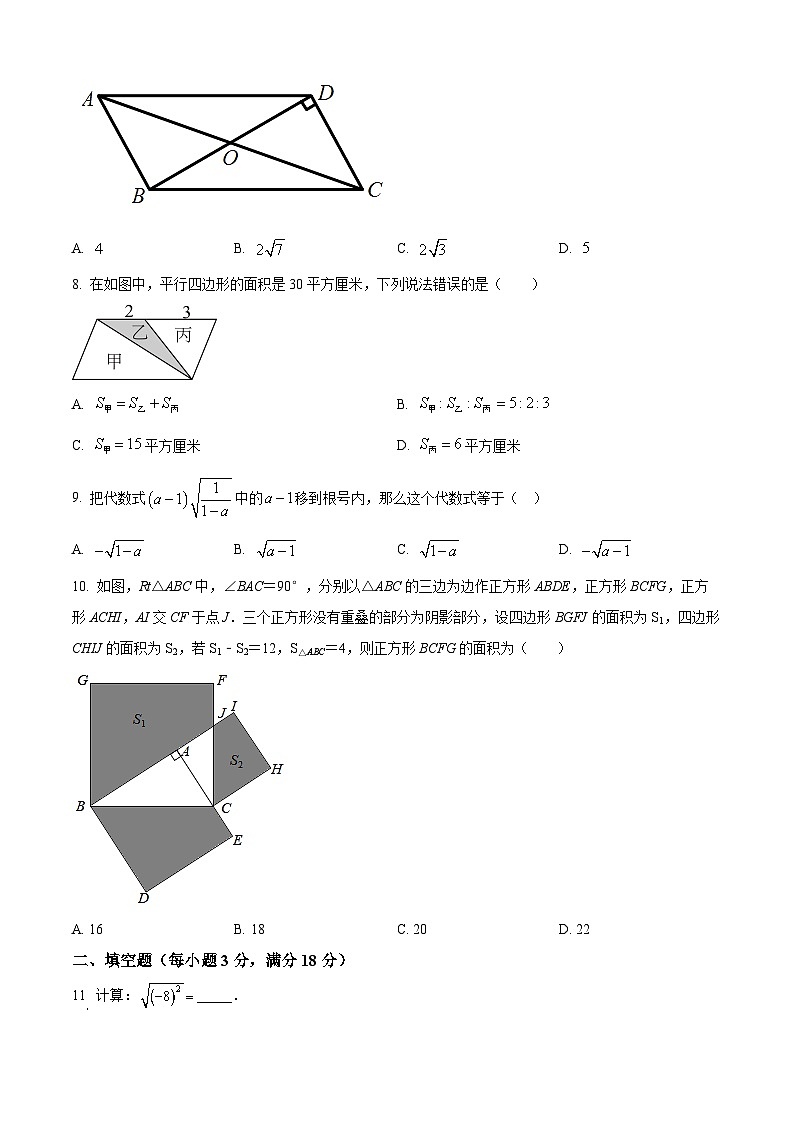
7. 如图，在中，交于点，则的长是（ ）
A. B. C. D.
8. 在如图中，平行四边形的面积是30平方厘米，下列说法错误的是（ ）

A. B.
C. 平方厘米D. 平方厘米
9. 把代数式中的移到根号内，那么这个代数式等于（ ）
A. B. C. D.
10. 如图，Rt△ABC中，∠BAC＝90°，分别以△ABC的三边为边作正方形ABDE，正方形BCFG，正方形ACHI，AI交CF于点J．三个正方形没有重叠的部分为阴影部分，设四边形BGFJ的面积为S1，四边形CHIJ的面积为S2，若S1﹣S2＝12，S△ABC＝4，则正方形BCFG的面积为（ ）
A. 16B. 18C. 20D. 22
二、填空题（每小题3分，满分18分）
11 计算：_____．
12. 如图，两条射线，点C，D分别在射线BN，AM上，只需添加一个条件，即可证明四边形ABCD是平行四边形，这个条件可以是____________（写出一个即可）．
13. 已知有理数满足，则的值为______．
14. 如图，在平面直角坐标系中，已知点A（0，8），B（﹣6，0），连接AB．将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则点C的坐标为 ___．
15. 如图，长方体的长为，宽为，高为，点在棱上，点离点的距离为，一只蚂蚁如果要沿着长方体的表面从点爬到点，需要爬行的最短路程是______．
16. 如图，和都是等腰直角三角形，若，，，则______．
三、解答题（满分72分）
17. 计算：
（1）；
（2）；
（3），为实数，且满足，求的算术平方根．
18. 直角三角形的三边长分别是6，8，，求这个三角形的周长．
19. 已知：如图，四边形中，，，，，，求四边形的面积．

20. 如图，E、F是平行四边形ABCD的对角线AC上的两点，且BE⊥AC，DF⊥AC，连接BE、ED、DF、FB．
（1）求证：四边形BEDF为平行四边形；
（2）若BE＝3，EF＝2，求BD的长．
21. 图1是超市购物车，图2为超市购物车侧面示意图，测得∠ACB=90°，支架AC=4.8dm，CB=3.6dm．
（1）两轮中心之间的距离为______dm；
（2）若的长度为dm，支点到底部的距离为5dm，试求的度数．
22. 阅读理解题：
像，，，两个含有二次根式的代数式相乘，积不含有二次根式，我们称这两个代数式互为有理化因式，例如：和，和，和等都是互为有理化因式，进行二次根式计算时，利用有理化因式，可以化去分母中的根号，请回答下列问题：
（1）化简：①______，②______；
（2）计算：；
（3）已知，，试比较，，的大小．
23. 如图，平面直角坐标系中，点在轴正半轴上，点在轴正半轴上，且，．
（1）的长为______；
（2）在轴上存在一点，使得最小，则最小值为______；
（3）在轴上否存在一点，使是直角三角形？若存在，求出点坐标．
24. 阅读下面材料：
小明遇到这样一个问题：如图1，在中，，平分，试判断和、之间的数量关系．
小明发现，利用轴对称做一个变化，在上截取，连接，得到一对全等的三角形，从而将问题解决（如图2）．
请回答：
（1）在图2中，小明得到的全等三角形是 ；
（2）和、之间的数量关系是 ．
参考小明思考问题的方法，解决问题：
如图3，在四边形中，平分，．求的长．