2024九年级数学下册第5章二次函数5.2二次函数的图像和性质2二次函数y=ax2＋ky=ax＋h2y=ax＋h2＋ka≠0的图像和性质课件新版苏科版

这是一份2024九年级数学下册第5章二次函数5.2二次函数的图像和性质2二次函数y=ax2＋ky=ax＋h2y=ax＋h2＋ka≠0的图像和性质课件新版苏科版，共34页。
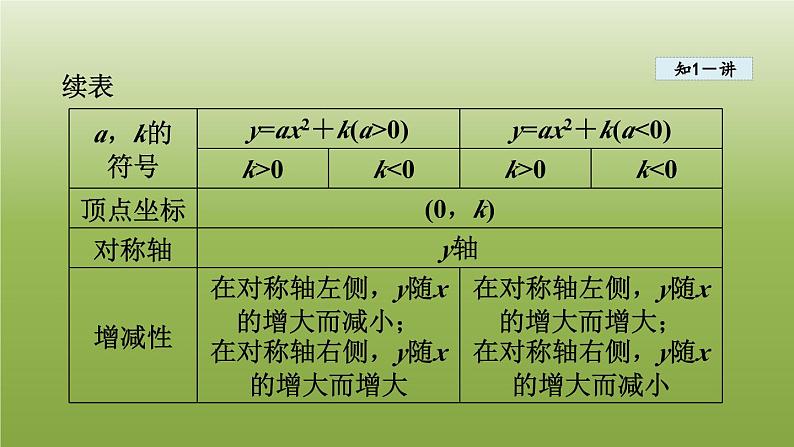
5.2 二次函数的图像和性质第5章 二次函数5.2.2 二次函数y=ax2＋k，y=a(x＋ h)2，y=a(x＋h)2＋k(a≠0)的 图像和性质逐点导讲练课堂小结作业提升课时讲解1课时流程2二次函数y=ax2＋k的图像和性质二次函数y=a(x＋h)2的图像和性质二次函数y=a(x＋h)2＋k的图像和性质二次函数y=ax2，y=ax2＋k，y=a(x＋h)2，y=a(x＋h)2＋k之间的关系知识点二次函数y=ax2＋k的图像和性质知1－讲11. 二次函数y=ax2＋k的图像与二次函数y=ax2的图像的关系它们的形状(开口大小、方向)相同，只是上、下位置不同，二次函数y=ax2＋k的图像可由二次函数y=ax2的图像上下平移|k|个单位长度得到.知1－讲2. 二次函数y=ax2＋k的图像与性质知1－讲续表知1－讲平移规律口诀上加下减，纵变横不变，“上加下减”表示抛物线的位置上下平移规律，即：抛物线y=ax2＋k是由抛物线y=ax2上下平移｜k｜个单位长度得到的，“上加”表示当k为正数时，向上平移；“下减”表示当k为负数时，向下平移；“纵变横不变”表示坐标的平移规律，即：抛物线平移时其对应点的纵坐标改变而横坐标不变.知1－练例 1(1)抛物线y=－2x2－5 的开口_______，对称轴是_______ ，顶点坐标是_________.解题秘方：紧扣抛物线的性质和平移规律求解.解：∵ y=－2x2－5 中a=－2 < 0，c=－5，∴抛物线开口向下，对称轴为y 轴，顶点坐标为 (0，－5).向下y轴(0，－5)知1－练(2)说出抛物线y=－2x2－5 与抛物线y=－2x2有什么关系？解题秘方：紧扣抛物线的性质和平移规律求解.解：抛物线y=－2x2－5 可由抛物线y=－2x2 向下平移5 个单位长度得到.知1－练技巧点拨本题可先画出抛物线的草图，如图5.2-4所示，然后根据图像的位置特征求解.知2－讲知识点二次函数y=a(x＋h)2的图像和性质21. 二次函数y=a(x＋h)2 的图像与二次函数y=ax2 的图像的关系它们的形状(开口大小、方向)相同，只是左、右位置不同，二次函数y=a(x＋h)2的图像可由二次函数y=ax2 的图像左右平移|h|个单位长度得到.知2－讲2. 二次函数y=a(x＋h)2 的图像与性质知2－讲续表知2－讲方法点拨平移规律：左加右减，横变纵不变.1. “左加”表示当h＞0时，函数y=a(x＋h)2的图像可以由函数y=ax2的图像向左平移h个单位长度得到.2. “右减”表示当h＜0时，函数y=a(x＋h)2的图像可以由函数y=ax2的图像向右平移|h|个单位长度得到.3. “横变纵不变”表示坐标的平移规律，即抛物线平移时对应点的横坐标改变而纵坐标不变.知2－练[模拟·南京] 抛物线y=－3(x－1)2的开口________，对称轴是________ ，顶点坐标是________.例2解题秘方：根据顶点式求抛物线的开口方向，对称轴及顶点坐标.解：由y=－3(x－1)2 可知，抛物线开口向下，对称轴为直线x=1，顶点坐标为(1，0).向下直线x=1(1，0)知2－练方法点拨当a>0时，抛物线开口向上，图像有最低点，当x=－h 时，y最小值=0；当a