初中学业水平考试数学模拟卷(一)含答案

这是一份初中学业水平考试数学模拟卷(一)含答案，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
★ 祝 考 试 顺 利 ★
一、选择题(共10题，每题3分，共30分．在每题给出的四个选项中，只有一项符合题目要求)
1．在我国古代著名的数学专著《九章算术》中，首次引入负数，如果一个物体向右移动10 m记作＋10，则－20表示（D）
A．向右移动10 m B．向左移动10 m
C．向右移动20 m D．向左移动20 m
2．下列图形是杭州亚运会部分比赛项目的图标，其中是轴对称图形的是（C）
A. B. C. D.
3．下列计算中正确的是（A）
A．x10·x＝x11 B．x8÷x2＝x4
C．3x＋5y＝8xy D．(x＋y)2＝x2＋y2
4．如图所示的立体图形，从上面看到的平面图形是（C）
A. B. C. D.
5．如图，直线a∥b，直角三角形的直角顶点在直线b上，已知∠1＝35°，则∠2的度数是（C）
A．35° B．45° C．55° D．65°
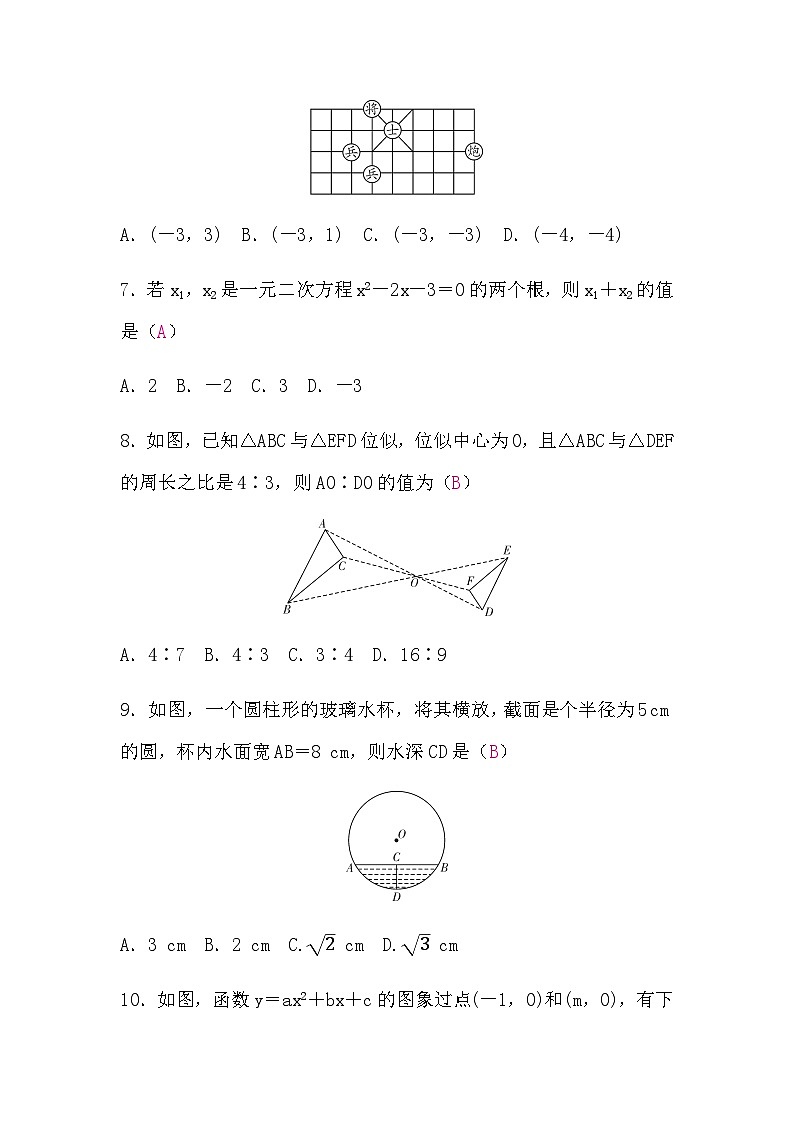
6．中国象棋具有悠久的历史，战国时期，就有了关于象棋的正式记载，如图是中国象棋棋局的一部分，如果用有序数对(2，1)表示“炮”的位置，(－2，2)表示“士”的位置，那么“将”的位置应表示为（A）
A．(－3，3) B．(－3，1) C．(－3，－3) D．(－4，－4)
7．若x1，x2是一元二次方程x2－2x－3＝0的两个根，则x1＋x2的值是（A）
A．2 B．－2 C．3 D．－3
8．如图，已知△ABC与△EFD位似，位似中心为O，且△ABC与△DEF的周长之比是4∶3，则AO∶DO的值为（B）
A．4∶7 B．4∶3 C．3∶4 D．16∶9
9．如图，一个圆柱形的玻璃水杯，将其横放，截面是个半径为5 cm的圆，杯内水面宽AB＝8 cm，则水深CD是（B）
A．3 cm B．2 cm C.eq \r(2) cm D.eq \r(3) cm
10．如图，函数y＝ax2＋bx＋c的图象过点(－1，0)和(m，0)，有下列结论：①abc1.
12．在一次函数y＝(k－1)x＋2的图象中，y随x的增大而增大，则k的值可以是2(答案不唯一)．(写出一个答案即可)
13．数学家斐波那契编写的《算经》中有如下问题：一组人平分10元钱，每人分得若干，若再加上6人，平分40元钱，则第二次每人所得与第一次相同，求这两次分钱的人数．答：(1)第一次分钱有2人；(2)第二次分钱有8人．
14．如图，电路图上有1个电源，4个开关和1个完好的小灯泡，随机闭合2个开关，则小灯泡发光的概率为eq \f(2,3).

15．如图，将矩形ABCD沿EM，FN折叠，点A，D分别与A′，D′对应，B，C两点对应点落在AD上的点G处，且GM⊥GN，如果S△A′EG＝8，S△D′GF＝2，那么AB的长为2eq \r(2).
【解析】由折叠的性质得出AB＝A′G＝D′G＝DC，证明△A′EG∽△D′GF，由相似三角形的性质得出eq \f(A′E,D′G)＝eq \f(A′G,D′F)，eq \f(S△A′EG,S△D′GF)＝eq \f(1,4)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(D′F,A′G)))eq \s\up12(2)，设D′F＝x，则D′G＝A′G＝2x，A′E＝4x，则可得出答案．
三、解答题(共9题，共75分，解答应写出文字说明、证明过程或演算步骤)
16．(6分)计算：eq \r(3,8)－eq \r(（－2）2)－(π－2)0＋|1－eq \r(3)|.
解：原式＝2－2－1＋eq \r(3)－1(4分)
＝eq \r(3)－2.(6分)
17．(6分)如图，已知CD是线段AB的垂直平分线，求证：∠CAD＝∠CBD.
证明：∵CD是线段AB的垂直平分线．
∴AD＝BD，AC＝BC，(2分)
在△ACD和△BCD中，eq \b\lc\{(\a\vs4\al\c1(AD＝BD，,AC＝BC，,CD＝CD，))
∴△ACD≌△BCD(SSS)，(4分)
∴∠CAD＝∠CBD.(6分)
18．(6分)某校拟派一名跳高运动员参加一项校际比赛，对甲、乙两名跳高运动员进行了 8次选拔比赛，他们的成绩(单位：m)如下：
甲：1.71，1.65，1.68，1.68，1.72，1.73，1.68，1.67；
乙：1.60，1.74，1.72，1.69，1.62，1.71，1.69，1.75.
【整理与分析】
(1)填空：a＝________，b＝________；
(2)这两人中，________的成绩更为稳定；
【判断与决策】
(3)经预测，跳高1.69 m就很可能获得冠军，该校为了获取跳高比赛冠军，可能选哪位运动员参赛？请说明理由．
解：(1)1.68(1分) 1.70(2分)
(2)甲(3分)
(3)应该选择乙，
理由：若1.69 m才能获得冠军，那么成绩在1.69 m 及1.69 m以上的次数乙多，
∴选择乙．(6分)
19．(8分)在一次数学综合实践活动中，某数学小组的同学们一起测量一座小山的高度．如图，在点A处测得山顶E的仰角为22.5°，向山的方向前进20 m，在点C处测得山顶E的仰角为45°，已知观测点A，C到地面的距离AB＝1.7 m，CD＝1.7 m．求小山EG的高度．(精确到0.1 m，参考数据：eq \r(2)≈1.414，sin 22.5°≈0.384，cs 22.5°≈0.925，tan 22.5°≈0.414)
解：延长AC交EG于点H，由题意得AH⊥EG，(2分)
∵EG⊥BG，CD⊥BG，∴四边形HGDC为矩形，
∴HG＝CD＝1.7 m，HC＝GD，(4分)
∵∠ECH＝45°，∠EAH＝22.5°，
∴∠CEA＝∠ECH－∠EAH＝22.5°，∴∠CEA＝∠EAH，∴EC＝AC＝20 m，(6分)
∵∠ECH＝45°，∴EH＝EC·sin∠ECH＝20×eq \f(\r(2),2)＝10eq \r(2)(m)，(7分)
∴EG＝EH＋HG＝10eq \r(2)＋1.7≈15.8(m)．
答：小山EG的高度约为15.8 m．(8分)
20．(8分)如图，一次函数y＝x＋3的图象与反比例函数y＝eq \f(k,x)(k≠0)的图象交于点A与点B(a，－1)．
(1)求反比例函数的解析式；
(2)若点P是第一象限内双曲线上的点(不与点A重合)，连接OP，且过点P作y轴的平行线，与直线AB相交于点C，连接OC，若△POC的面积为3，求点P的坐标．
解：(1)将B(a，－1)代入一次函数y＝x＋3中，得a＝－4，
∴B(－4，－1)，(1分)
将B(－4，－1)代入反比例函数y＝eq \f(k,x)(k≠0)中，得k＝4，
∴反比例函数的解析式为y＝eq \f(4,x).(2分)
(2)设点P的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(m，\f(4,m)))(m>0)，则C(m，m＋3)，(3分)
∴PC＝|eq \f(4,m)－(m＋3)|，点O到直线PC的距离为m，(5分)
∴S△POC＝eq \f(1,2)m×|eq \f(4,m)－(m＋3)|＝3，(6分)
解得m＝－1或－2或－5或2，
又∵m>0，∴m＝2.
∴点P的坐标为(2，2)．(8分)
21．(8分)如图，AB是⊙O的直径，C，D是⊙O上两点，∠ABD＝2∠A，过C作CE⊥DB交DB的延长线于点E.
(1)求证：CE是⊙O的切线；
(2)若tan A＝eq \f(1,2)，⊙O的半径为eq \r(5)，求CD的长．
(1)证明：连接OC，∴∠COB＝2∠A，(1分)
∵∠ABD＝2∠A，∴∠ABD＝∠COB，∴DB∥OC，
∵CE⊥DB，∴OC⊥CE，(2分)
∵OC为⊙O的半径，∴CE是⊙O的切线．(3分)
(2)解：连接BC，∵AB为⊙O的直径，
∴∠ACB＝90°，∴tan A＝eq \f(BC,AC)，
∵tan A＝eq \f(1,2)，∴eq \f(BC,AC)＝eq \f(1,2)，∴AC＝2BC，(4分)
∵⊙O的半径为eq \r(5)，∴AB＝2eq \r(5)，
在Rt△ABC中，AB2＝AC2＋BC2，∴(2eq \r(5))2＝4BC2＋BC2，
∵BC>0，∴BC＝2，AC＝4，(5分)
∵∠OCE＝90°，∴∠BCE＋∠OCB＝90°，∠A＋∠OBC＝90°，
又∵OC＝OB，∴∠OCB＝∠OBC，∴∠BCE＝∠A，(6分)
在Rt△BCE中，tan∠BCE＝eq \f(BE,EC)＝tan A＝eq \f(1,2)，
∴EC＝2BE，BC2＝BE2＋CE2，22＝BE2＋4BE2，
∵BE>0，∴BE＝eq \f(2\r(5),5)，CE＝eq \f(4\r(5),5).(7分)
又∵∠A＝∠D，∴tan D＝eq \f(CE,DE)＝tan A＝eq \f(1,2)，∴DE＝eq \f(8\r(5),5)，
∴CD＝4.(8分)
22.(10分)杭州亚运会期间，某网店经营亚运会吉祥物“宸宸、琮琮和莲莲”钥匙扣礼盒装，每盒进价为25元，出于营销考虑，要求每盒商品的售价不低于25元且不高于38元，在销售过程中发现该商品每周的销售量y(单位：件)与销售单价x(单位：元)之间满足一次函数关系：当销售单价为33元时，销售量为34件；当销售单价为35元时，销售量为30件．
(1)请求出y与x的函数关系式；
(2)设该网店每周销售这种商品所获得的利润为w元，
①写出w与x的函数关系式；
②将该商品销售单价定为多少元时，才能使网店每周销售该商品所获利润最大？最大利润是多少？
解：(1)y与x的函数关系式为y＝－2x＋100.(2分)
(2)①由题意可得w＝(x－25)(－2x＋100)＝－2x2＋150x－2 500.
∴w与x的函数关系式为w＝－2x2＋150x－2 500.(4分)
②w＝－2x2＋150x－2 500，
∵－2