


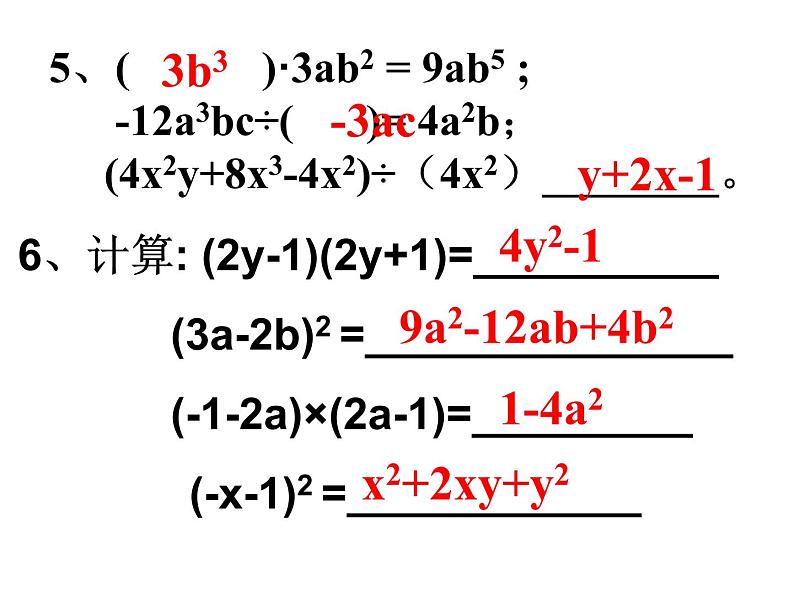



还剩7页未读,
继续阅读
第3章 整式的乘除复习 浙教版七年级数学下册课件
展开
这是一份第3章 整式的乘除复习 浙教版七年级数学下册课件,共14页。
第三章整式的乘除复习主要知识点:1、整数指数幂及其运算的法则:① am·an=am+n③ (am)n=amn④ (ab)n=anbn ⑤ a0=1 (a≠0)2、计算: a·a2+a3 =__________.3、计算:a2·(ab)3 =_____.1、计算: 3a+2a = ____; 3a·2a =____; 3a÷(2a )=____; a2·a2 =______; a3 ÷a2 =___; (-3ab2)2 =______.5a6a21.5a4a9a2b44、x3 · x-3 = ___;a6÷a2 · a3 =___; 20 + 2-1 =______1a73/26、计算: (2y-1)(2y+1)=__________ (3a-2b)2 =_______________ (-1-2a)×(2a-1)=_________ (-x-1)2 =____________5、( )·3ab2 = 9ab5 ; -12a3bc÷( )= 4a2b; (4x2y+8x3-4x2)÷(4x2)________。3b3-3acy+2x-14y2-19a2-12ab+4b21-4a2x2+2xy+y27、若a2+b2=5,ab=2,则 (a+b)2 =____, (a-b)2 =_____.8、已知x2+y2=25,x+y=7,则(x-y)2的值等于_________.91110.若x2 -6x+m2是一个完全平方式,则m =( ) A.-3 B.3 C.±3 D.9变式:若x2 +mx+9是一个完全平方式,则m = 若x2 -mx+9是一个完全平方式,则m =11.如果(x+3)(x+m)中不含的x的一次项,那么 m 的值为( )A.-3 B.3 C.0 D.1 CA12、已知a=0.05x+19,b=0.05x+20, c =0.05x+21,则代数式 a2+b2+c2-ab-bc-ca的值是( ) A. 4 B.3 C.2 D.113.若a,b都是有理数且 a2+b2+4a-9b+13=0,则2ab的值等于( )A. -6 B. 6 C.-12 D.12CB14、用科学记数法表示0.00000320得( ) A 3.20×10-5 B 3.2×10-6 C 3.2×10-7 D 3.20×10-6 D15、小数表示: 1.27×10-7=_________;0.00000012716、一个单项式与-3x3y3的积是12x5y4,则这个单项式为______;17、要使(x-2)0有意义,则x应满足的条件是_______;18、圆的半径增加到原来的2倍,那么它的面积增加到原来的___倍;-4x2yx≠2419、已知四个数:3-2,-32,30,-3-3其中最大的数是( ) A 3-2 B -32 C 30 D -3-3 C20、用简便方法计算: 20192-2018×2020能力挑战 你能用简便的方法计算下列各题:若Xa=2, yb=3, 求(x3a+2b)2的值.注意幂的运算法则逆用 能力挑战:已知10m=4,10n=5.求103m+2n+1的值. 已知162×43×26=22a+1,(102)b=1012,求a+b的值。比较750与4825的大小.
第三章整式的乘除复习主要知识点:1、整数指数幂及其运算的法则:① am·an=am+n③ (am)n=amn④ (ab)n=anbn ⑤ a0=1 (a≠0)2、计算: a·a2+a3 =__________.3、计算:a2·(ab)3 =_____.1、计算: 3a+2a = ____; 3a·2a =____; 3a÷(2a )=____; a2·a2 =______; a3 ÷a2 =___; (-3ab2)2 =______.5a6a21.5a4a9a2b44、x3 · x-3 = ___;a6÷a2 · a3 =___; 20 + 2-1 =______1a73/26、计算: (2y-1)(2y+1)=__________ (3a-2b)2 =_______________ (-1-2a)×(2a-1)=_________ (-x-1)2 =____________5、( )·3ab2 = 9ab5 ; -12a3bc÷( )= 4a2b; (4x2y+8x3-4x2)÷(4x2)________。3b3-3acy+2x-14y2-19a2-12ab+4b21-4a2x2+2xy+y27、若a2+b2=5,ab=2,则 (a+b)2 =____, (a-b)2 =_____.8、已知x2+y2=25,x+y=7,则(x-y)2的值等于_________.91110.若x2 -6x+m2是一个完全平方式,则m =( ) A.-3 B.3 C.±3 D.9变式:若x2 +mx+9是一个完全平方式,则m = 若x2 -mx+9是一个完全平方式,则m =11.如果(x+3)(x+m)中不含的x的一次项,那么 m 的值为( )A.-3 B.3 C.0 D.1 CA12、已知a=0.05x+19,b=0.05x+20, c =0.05x+21,则代数式 a2+b2+c2-ab-bc-ca的值是( ) A. 4 B.3 C.2 D.113.若a,b都是有理数且 a2+b2+4a-9b+13=0,则2ab的值等于( )A. -6 B. 6 C.-12 D.12CB14、用科学记数法表示0.00000320得( ) A 3.20×10-5 B 3.2×10-6 C 3.2×10-7 D 3.20×10-6 D15、小数表示: 1.27×10-7=_________;0.00000012716、一个单项式与-3x3y3的积是12x5y4,则这个单项式为______;17、要使(x-2)0有意义,则x应满足的条件是_______;18、圆的半径增加到原来的2倍,那么它的面积增加到原来的___倍;-4x2yx≠2419、已知四个数:3-2,-32,30,-3-3其中最大的数是( ) A 3-2 B -32 C 30 D -3-3 C20、用简便方法计算: 20192-2018×2020能力挑战 你能用简便的方法计算下列各题:若Xa=2, yb=3, 求(x3a+2b)2的值.注意幂的运算法则逆用 能力挑战:已知10m=4,10n=5.求103m+2n+1的值. 已知162×43×26=22a+1,(102)b=1012,求a+b的值。比较750与4825的大小.
相关资料
更多









