






还剩15页未读,
继续阅读
第4章 因式分解复习课 北师大版八年级数学下册课件
展开
这是一份第4章 因式分解复习课 北师大版八年级数学下册课件,共23页。
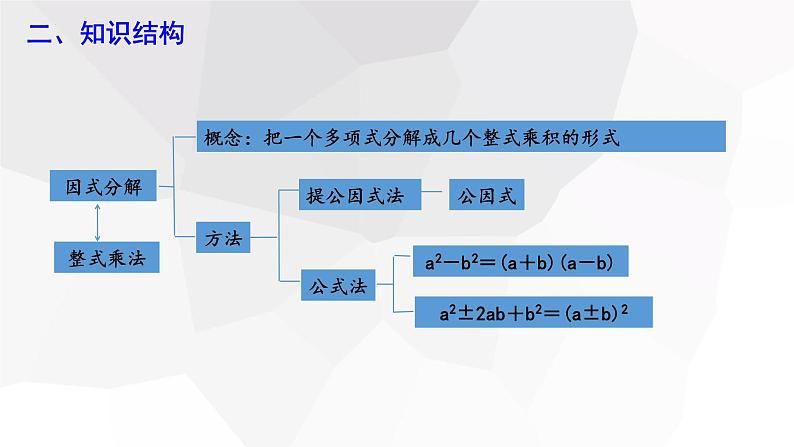
第四章 因式分解复习课1.理解因式分解的概念,并能根据因式分解与整式乘法的关系解题2.知道因式分解的方法、步骤,并能熟练应用因式分解的各种方法进行因式分解3.能利用因式分解的方法解决实际问题一、学习目标二、知识结构三、知识回顾知识点一 因式分解的概念1.把一个多项式分解成几个整式乘积的形式,叫做多项式的因式分解.3.多项式的因式分解是一个恒等变形.2.因式分解的结果必须是几个整式乘积的形式;注意:1.等号的左边必须是一个多项式;2.多项式的因式分解与乘法运算是相反的变形过程.例1.下列式子中,从左往右的变形是因式分解且正确的有哪些.(1)x2-xy2=x(x-y)2 ;(2)(x+2)2=x2+4x+4;(3)4x2+2xy+y2=(2x+y)2 ;(4)4xy2=2xy·2y;(5)ax2-bx=x(ax-b).(4)的对象为单项式分析:因式分解的对象:多项式;因式分解的结果:几个整式的乘积;因式分解的正确性可根据整式乘法来验证.(2)结果为多项式(1)(3)等式左右两边不相等解:因式分解且正确的有(5)典型例题【当堂检测】1.下列从左边到右边的变形,是正确的因式分解的是( ) A.(x+1)(x-1)=x2-1 B.x2-4y2 =(x+4y)(x-4y) C.x2-6x+9=(x-3)2 D.x2-2x+1=x(x-2)+1C知识点二 因式分解的方法三、知识回顾1.提公因式法分解因式(1)确定公因式:当多项式的各项系数都是整数时,公因式的系数应取各项系数的最大公约数,字母应取各项相同的字母,且相同字母的指数取次数最低的.(2)把公因式写在括号外面,将多项式写成整式乘积的形式.三、知识回顾2.公式法分解因式(1)因式分解中的平方差公式:a2-b2=(a+b)(a-b);平方差式的特征:①可化为两个整式;②两项符号相反;③每一项都是整式的平方.(2)因式分解中的完全平方公式:a2±2ab+b2=(a±b)2;完全平方式的特征:①可化成三项式;②有两项符号相同,能写成两个整式的平方的形式;③另一项是这两整式乘积的±2倍.解:例2.分解因式:(1)8ax2-18ay (2)x2-9y2 (3)4x2-12xy+9y2分析:根据数据特征选择合适方法进行因式分解.=2a(4x2-9y)(3)原式=(2x)2-2×2x·3y+(3y)2=(2x-3y)2(1)原式=2a·4x2-2a·9y(2)原式=x2-(3y)2=(x+3y)(x-3y)典型例题例3.分解因式: (1)2m(a+b)2-2m(a-1)2 (2)a(x+y)2-2a(x+y)+a =2m[(a+b)+(a-1)][(a+b)-(a-1)](2)原式=a[(x+y)2-2(x+y)+1]=a(x+y-1)2解:(1)原式=2m[(a+b)2-(a-1)2]=2m(2a+b-1)(b+1)典型例题因式分解过程中:有公因式,先提公因式例3.分解因式: (3)(y2-1)2+6(1-y2)+9 (4)(a2+b2)2-4a2b2 =(y2-1-3)2(4)原式=(a2+b2)2-(2ab)2=(a2+b2+2ab)(a2+b2-2ab)解:(3)原式=(y2-1)2-6(y2-1)+9=(y2-4)2典型例题=(a+b)2(a-b)2=(y+2)2(y-2)2因式分解要分解彻底【当堂检测】2.分解因式:(1)a(x-y)-b(x-y)-c(y-x)= ;(2)(m-n)2-(n-m)(m-2n)= ;(3)3x3-27xy2= ;(4)3x2y+12xy2+12y3= .(x-y)(a-b+c)(m-n)(2m-3n)3x(x+3y)(x-3y)3y(x+2y)2【当堂检测】3.分解因式.(1) 2a(x-y)+4b(x-y) (2)a2+2ab+b2-c2=(a+b+c)(a+b-c)解:(1)原式=2(x-y)(a+2b)(2)原式=(a+b)2-c2(3)18xy2 -27x2y-3y3 (4)3x3y-3xy3=-3y(3x-y)2=3xy(x+y)(x-y)(3)原式=-3y(9x2-6xy+y2)(4)原式=3xy(x2-y2)4.计算:(1)5752×6-4252×6; (2)20192-2018×2020-9992【当堂检测】解:(1)原式=6×(5752-4252)=(1+999)×(1-999)=6×1000×150=6×(575+425)×(575-425)(2)原式=20192-(2019-1)×(2019+1)-9992=20192-(20192-1)-9992=1-9992=1000×(-998)=-998000=9000005.若a-b=-7,ab=-2,求下列各式的值:(1)a2b3-a3b2; (2)a3b-2a2b2+ab3.【当堂检测】解:(1)a2b3-a3b2=a2b2(b-a)=ab(a-b)2(2)a3b-2a2b2+ab3=ab(a2-2ab+b2)∵a-b=-7,ab=-2∴原式=(-2)2×7=28∵a-b=-7,ab=-2∴原式=(-2)×(-7)2=-98归纳总结:在代数式求值问题中,解题的基本思路是先化简代数式,把代数式化简至最简后再代入求值.但在不同问题中,化简的方法也不同,如:利用整式的加减、整式的乘法、分解因式等,因此,应根据具体的题目特点,灵活选用化简代数式的方法.【当堂检测】典型例题例4.小戴同学动手剪了若干张如图所示的正方形与长方形纸片.①拼成如图(b)所示的正方形,根据四张小纸片的面积之和等于大纸片(正方形)的面积,有a2+2ab+b2=(a+b)2,验证了完全平方公式(分解因式);典型例题②拼成如图(c)所示的长方形,可得a2+3ab+2b2=(a+2b)(a+b),多项式a2+3ab+2b2分解因式的结果表示长方形长、宽的两个整式a+2b与a+b的积.问题:(1)自己动手试一试,利用拼图分解因式2a2+3ab+b2= .(2)猜想面积为2a2+5ab+2b2的长方形的长、宽可能分别为: .(2a+b)(a+b)a+2b,2a+b或2a+b,a+2b典型例题归纳总结:本章中数形结合思想主要体现在用长方形纸片的图形面积来解释因式分解.利用几何图形的面积可以把整式乘法与因式分解有机地联系起来.拓展:由整式的乘法得(x+p)(x+q)=x2+(p+q)x+pq;那么反过来x2+(p+q)x+pq=(x+p)(x+q)也成立,在拼图过程中也验证了该式.那么除了利用拼图将a2+5ab+6b2分解因式,也可以用如下方法:a2+5ab+6b2=a2+(2b+3b)a+2b·3b=(a+2b)(a+3b).【当堂检测】(1)x2-3x-10; (2)x2﹣8x+12.解:(1)原式=x2+[2+(-5)]x+2×(-5)(2)原式=x2+[(-2)+(-6)]+(-2)×(-6)6.因式分解.=(x+2)(x-5)=(x-2)(x-6)典型例题例5.如图,100个正方形由小到大套在一起,从外向里相间画上阴影,最里面一个小正方形没有画阴影,最外面一层画阴影,最外面的正方形的边长为100cm,向里依次为99cm,98cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?分析:每一块阴影的面积可以表示成相邻正方形的面积的差解:S阴影 =(1002-992)+(982-972)+…+(22-12) =(100-99)(100+99)+(98-97)(98+97)+…+(2-1)(2+1) =100+99+98+97+…+2+1 =5050答:所有阴影部分的面积和是5050cm2.7.如图所示的圆形工件,大圆的半径R为65.4mm,四个小圆的半径r为17.3mm,求图中阴影部分的面积.解:S阴影=S大圆-4S小圆=π(R+2r)(R-2r)=π(65.4+2×17.3)(65.4-2×17.3)=π×100×30.8答:图中阴影部分的面积为3080πmm2.=πR2-4πr2=π(R2-4r2)【当堂检测】=3080π四、课堂总结
第四章 因式分解复习课1.理解因式分解的概念,并能根据因式分解与整式乘法的关系解题2.知道因式分解的方法、步骤,并能熟练应用因式分解的各种方法进行因式分解3.能利用因式分解的方法解决实际问题一、学习目标二、知识结构三、知识回顾知识点一 因式分解的概念1.把一个多项式分解成几个整式乘积的形式,叫做多项式的因式分解.3.多项式的因式分解是一个恒等变形.2.因式分解的结果必须是几个整式乘积的形式;注意:1.等号的左边必须是一个多项式;2.多项式的因式分解与乘法运算是相反的变形过程.例1.下列式子中,从左往右的变形是因式分解且正确的有哪些.(1)x2-xy2=x(x-y)2 ;(2)(x+2)2=x2+4x+4;(3)4x2+2xy+y2=(2x+y)2 ;(4)4xy2=2xy·2y;(5)ax2-bx=x(ax-b).(4)的对象为单项式分析:因式分解的对象:多项式;因式分解的结果:几个整式的乘积;因式分解的正确性可根据整式乘法来验证.(2)结果为多项式(1)(3)等式左右两边不相等解:因式分解且正确的有(5)典型例题【当堂检测】1.下列从左边到右边的变形,是正确的因式分解的是( ) A.(x+1)(x-1)=x2-1 B.x2-4y2 =(x+4y)(x-4y) C.x2-6x+9=(x-3)2 D.x2-2x+1=x(x-2)+1C知识点二 因式分解的方法三、知识回顾1.提公因式法分解因式(1)确定公因式:当多项式的各项系数都是整数时,公因式的系数应取各项系数的最大公约数,字母应取各项相同的字母,且相同字母的指数取次数最低的.(2)把公因式写在括号外面,将多项式写成整式乘积的形式.三、知识回顾2.公式法分解因式(1)因式分解中的平方差公式:a2-b2=(a+b)(a-b);平方差式的特征:①可化为两个整式;②两项符号相反;③每一项都是整式的平方.(2)因式分解中的完全平方公式:a2±2ab+b2=(a±b)2;完全平方式的特征:①可化成三项式;②有两项符号相同,能写成两个整式的平方的形式;③另一项是这两整式乘积的±2倍.解:例2.分解因式:(1)8ax2-18ay (2)x2-9y2 (3)4x2-12xy+9y2分析:根据数据特征选择合适方法进行因式分解.=2a(4x2-9y)(3)原式=(2x)2-2×2x·3y+(3y)2=(2x-3y)2(1)原式=2a·4x2-2a·9y(2)原式=x2-(3y)2=(x+3y)(x-3y)典型例题例3.分解因式: (1)2m(a+b)2-2m(a-1)2 (2)a(x+y)2-2a(x+y)+a =2m[(a+b)+(a-1)][(a+b)-(a-1)](2)原式=a[(x+y)2-2(x+y)+1]=a(x+y-1)2解:(1)原式=2m[(a+b)2-(a-1)2]=2m(2a+b-1)(b+1)典型例题因式分解过程中:有公因式,先提公因式例3.分解因式: (3)(y2-1)2+6(1-y2)+9 (4)(a2+b2)2-4a2b2 =(y2-1-3)2(4)原式=(a2+b2)2-(2ab)2=(a2+b2+2ab)(a2+b2-2ab)解:(3)原式=(y2-1)2-6(y2-1)+9=(y2-4)2典型例题=(a+b)2(a-b)2=(y+2)2(y-2)2因式分解要分解彻底【当堂检测】2.分解因式:(1)a(x-y)-b(x-y)-c(y-x)= ;(2)(m-n)2-(n-m)(m-2n)= ;(3)3x3-27xy2= ;(4)3x2y+12xy2+12y3= .(x-y)(a-b+c)(m-n)(2m-3n)3x(x+3y)(x-3y)3y(x+2y)2【当堂检测】3.分解因式.(1) 2a(x-y)+4b(x-y) (2)a2+2ab+b2-c2=(a+b+c)(a+b-c)解:(1)原式=2(x-y)(a+2b)(2)原式=(a+b)2-c2(3)18xy2 -27x2y-3y3 (4)3x3y-3xy3=-3y(3x-y)2=3xy(x+y)(x-y)(3)原式=-3y(9x2-6xy+y2)(4)原式=3xy(x2-y2)4.计算:(1)5752×6-4252×6; (2)20192-2018×2020-9992【当堂检测】解:(1)原式=6×(5752-4252)=(1+999)×(1-999)=6×1000×150=6×(575+425)×(575-425)(2)原式=20192-(2019-1)×(2019+1)-9992=20192-(20192-1)-9992=1-9992=1000×(-998)=-998000=9000005.若a-b=-7,ab=-2,求下列各式的值:(1)a2b3-a3b2; (2)a3b-2a2b2+ab3.【当堂检测】解:(1)a2b3-a3b2=a2b2(b-a)=ab(a-b)2(2)a3b-2a2b2+ab3=ab(a2-2ab+b2)∵a-b=-7,ab=-2∴原式=(-2)2×7=28∵a-b=-7,ab=-2∴原式=(-2)×(-7)2=-98归纳总结:在代数式求值问题中,解题的基本思路是先化简代数式,把代数式化简至最简后再代入求值.但在不同问题中,化简的方法也不同,如:利用整式的加减、整式的乘法、分解因式等,因此,应根据具体的题目特点,灵活选用化简代数式的方法.【当堂检测】典型例题例4.小戴同学动手剪了若干张如图所示的正方形与长方形纸片.①拼成如图(b)所示的正方形,根据四张小纸片的面积之和等于大纸片(正方形)的面积,有a2+2ab+b2=(a+b)2,验证了完全平方公式(分解因式);典型例题②拼成如图(c)所示的长方形,可得a2+3ab+2b2=(a+2b)(a+b),多项式a2+3ab+2b2分解因式的结果表示长方形长、宽的两个整式a+2b与a+b的积.问题:(1)自己动手试一试,利用拼图分解因式2a2+3ab+b2= .(2)猜想面积为2a2+5ab+2b2的长方形的长、宽可能分别为: .(2a+b)(a+b)a+2b,2a+b或2a+b,a+2b典型例题归纳总结:本章中数形结合思想主要体现在用长方形纸片的图形面积来解释因式分解.利用几何图形的面积可以把整式乘法与因式分解有机地联系起来.拓展:由整式的乘法得(x+p)(x+q)=x2+(p+q)x+pq;那么反过来x2+(p+q)x+pq=(x+p)(x+q)也成立,在拼图过程中也验证了该式.那么除了利用拼图将a2+5ab+6b2分解因式,也可以用如下方法:a2+5ab+6b2=a2+(2b+3b)a+2b·3b=(a+2b)(a+3b).【当堂检测】(1)x2-3x-10; (2)x2﹣8x+12.解:(1)原式=x2+[2+(-5)]x+2×(-5)(2)原式=x2+[(-2)+(-6)]+(-2)×(-6)6.因式分解.=(x+2)(x-5)=(x-2)(x-6)典型例题例5.如图,100个正方形由小到大套在一起,从外向里相间画上阴影,最里面一个小正方形没有画阴影,最外面一层画阴影,最外面的正方形的边长为100cm,向里依次为99cm,98cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?分析:每一块阴影的面积可以表示成相邻正方形的面积的差解:S阴影 =(1002-992)+(982-972)+…+(22-12) =(100-99)(100+99)+(98-97)(98+97)+…+(2-1)(2+1) =100+99+98+97+…+2+1 =5050答:所有阴影部分的面积和是5050cm2.7.如图所示的圆形工件,大圆的半径R为65.4mm,四个小圆的半径r为17.3mm,求图中阴影部分的面积.解:S阴影=S大圆-4S小圆=π(R+2r)(R-2r)=π(65.4+2×17.3)(65.4-2×17.3)=π×100×30.8答:图中阴影部分的面积为3080πmm2.=πR2-4πr2=π(R2-4r2)【当堂检测】=3080π四、课堂总结
相关资料
更多









