2024年甘肃省金昌市永昌六中九年级中考第一次仿真模拟考试 数学模拟预测题（原卷版+解析版）

这是一份2024年甘肃省金昌市永昌六中九年级中考第一次仿真模拟考试 数学模拟预测题（原卷版+解析版），文件包含2024年甘肃省金昌市永昌六中九年级中考第一次仿真模拟考试数学模拟预测题原卷版docx、2024年甘肃省金昌市永昌六中九年级中考第一次仿真模拟考试数学模拟预测题解析版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

考生注意：本试卷共120分，考试时间120分钟．
一、选择题：本大题共10小题，每小题3分，共30分．
1. 与2024互为相反数是（ ）
A. 2024B. C. D.
【答案】B
【解析】
【分析】本题考查了相反数的定义，解答本题的关键是熟练掌握相反数的定义，根据只有符号不同的两个数是互为相反数解答即可．
【详解】解：2024互为相反数是．
故选B．
2. 据国家统计局数据，2023年中国国内生产总值约1260000亿元．将1260000用科学记数法表示为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查科学记数法．科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值时，n是正数；当原数的绝对值时，n是负数．
【详解】解：将1260000用科学记数法表示为．
故选：D．
3. 如图，三角板的直角顶点在直尺的一边上．若，，则的度数是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】如图所示，根据，先算出的度数，根据邻补角再算出的度数，根据三角形内角和即可求解．
【详解】解：如图所示，
直尺中，，
∴，
∵，
∴，
∵，，
∴，
故选：．
【点睛】本题主要考查平行线，邻补角，三角形内角和的综合，掌握平行线的性质，三角形的内角和定理是解题的关键．
4. 下列运算正确的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】本题考查整式的运算，根据合并同类项法则、幂的运算法则、完全平方公式和同底数幂的除法运算法则逐项判断即可解答．
【详解】解：A、和不是同类项，不能加减，故原计算错误，不符合题意；
B、，计算正确，符合题意；
C、，故原计算错误，不符合题意；
D、，故原计算错误，不符合题意；
故选：B．
5. 如图所示，该几何体的俯视图为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据从上边看得到的图形是俯视图，可得答案．
【详解】解：从上边看是一些等宽的矩形，其中有两条宽是虚线，
故选：C．
【点睛】本题考查了简单组合体的三视图，从上边看得到的图形是俯视图．
6. 不等式组的解在数轴上表示为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】先解每一个不等式，再根据结果判断数轴表示的正确方法．
【详解】解：由不等式①，得3x＞5-2，解得x＞1，
由不等式②，得-2x≥1-5，解得x≤2，
∴数轴表示的正确方法为C．
故选：C．
【点睛】考核知识点：解不等式组.
7. 《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响．该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元．问有多少人?该物品价几何?设有x人．物品价值y元，则列方程组为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据题意找到等量关系：人数×8−3＝物品价值；人数×7＋4＝物品价值，把等量关系用方程组表示出来即可．
【详解】解：设有人，物品价值元，由题意得：
，
故选：D．
【点睛】此题主要考查二元一次方程组解决实际应用题，关键是正确理解题意，找出题目中的等量关系．
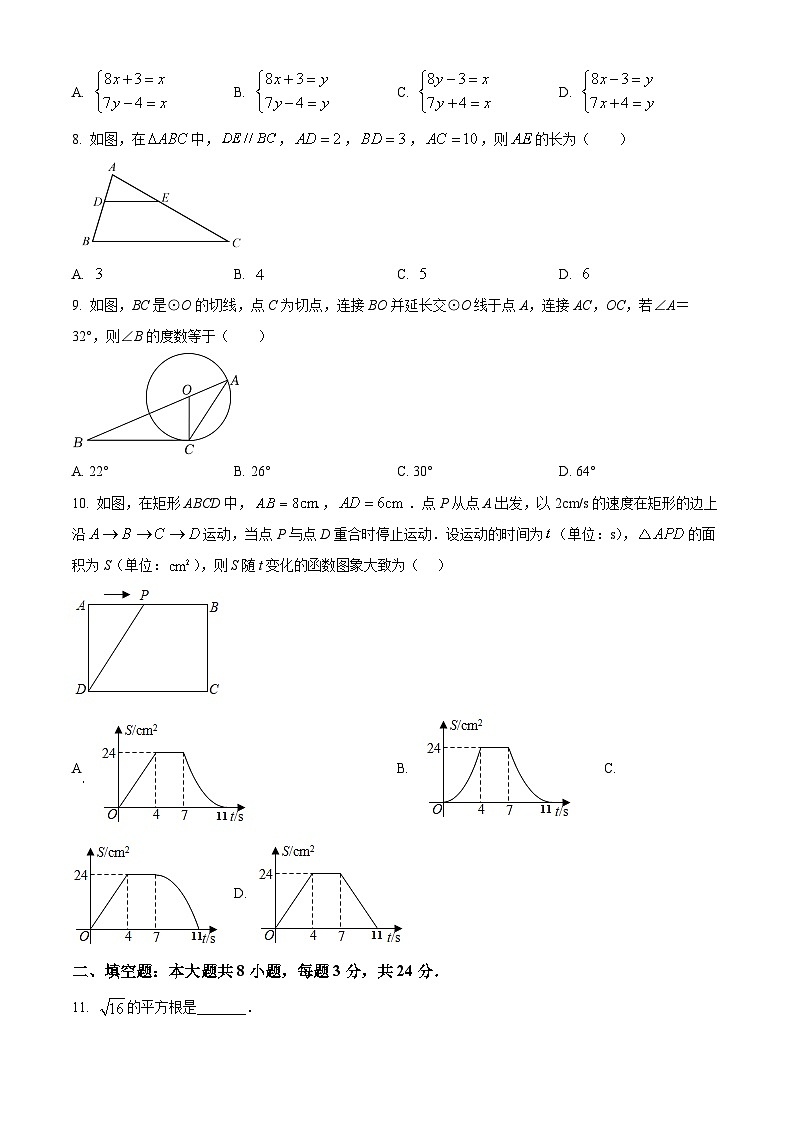
8. 如图，在中，，，，，则的长为（ ）
A. B. C. D.
【答案】B
【解析】
【分析】由，得，进而即可求解．
【详解】解：∵在中，，，，，
∴，即：，
∴AE=4，
故选B．
【点睛】本题主要考查平行线分线段成比例定理，列出比例式，是解题的关键．
9. 如图，BC是⊙O的切线，点C为切点，连接BO并延长交⊙O线于点A，连接AC，OC，若∠A＝32°，则∠B的度数等于（ ）
A. 22°B. 26°C. 30°D. 64°
【答案】B
【解析】
【分析】先根据圆周角定理求出，再根据切线的性质得到，然后根据直角三角形的两锐角互余即可得．
详解】解：由圆周角定理得：，
是的切线，
，
，
故选：B．
【点睛】本题考查了圆周角定理、圆的切线的性质等知识点，熟练掌握圆周角定理和圆的切线的性质是解题关键．
10. 如图，在矩形ABCD中，，．点P从点A出发，以2cm/s的速度在矩形的边上沿运动，当点P与点D重合时停止运动．设运动的时间为（单位：s），的面积为S（单位：），则S随t变化的函数图象大致为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】分点P在AB上运动, 0≤t≤4；点P在BC上运动, 4＜t≤7；点P在CD上运动, 7＜t≤11，分别计算即可
【详解】当点P在AB上运动时, S==6t，0≤t≤4；
当点P在BC上运动时, S==24，4＜t≤7；
点P在CD上运动, S=， 7＜t≤11，
故选D．
【点睛】本题考查了矩形中的动点面积函数图像问题，正确进行分类，清楚函数图像的性质是解题的关键．
二、填空题：本大题共8小题，每题3分，共24分．
11. 的平方根是_______．
【答案】±2
【解析】
【详解】解：∵
∴的平方根是±2．
故答案为±2．
12. 因式分解： ________________．
【答案】
【解析】
【分析】此题主要考查了提取公因式法与公式法的综合运用，正确运用平方差公式是解题关键．首先提取公因式3，再利用平方差公式分解因式即可．
【详解】解：原式
．
故答案为：．
13. 若关于x一元二次方程有实数根，则k的取值范围是_______．
【答案】且
【解析】
【分析】先根据一元二次方程定义和根的判别式的意义得到且，然后求出两不等式的公共部分即可．
【详解】解：∵关于x的一元二次方程有实数根，
∴且，
解得且．
故答案为：且．
【点睛】本题考查了根的判别式：一元二次方程的根与有如下关系：当时，方程有两个不相等的实数根；当时，方程有两个相等的实数根；当时，方程无实数根．上面的结论反过来也成立．
14. 若二次函数的图象经过点，则________．
【答案】2025
【解析】
【分析】本题考查了二次函数的图象及性质，将点代入可得，进而可求解，熟练掌握基础知识是解题的关键．
【详解】解：依题意得：，
即：，
，
故答案为：2025．
15. 如图，正六边形ABCDEF的边长为2，以顶点A为圆心，AB的长为半径画圆，则图中阴影部分的面积为______．
【答案】##
【解析】
【分析】延长FA交⊙A于G，如图所示：根据六边形ABCDEF是正六边形，AB=2，利用外角和求得∠GAB=，再求出正六边形内角∠FAB=180°-∠GAB=180°-60°=120°， 利用扇形面积公式代入数值计算即可．
【详解】解：延长FA交⊙A于G，如图所示：
∵六边形ABCDEF是正六边形，AB=2，
∴∠GAB=，
∠FAB=180°-∠GAB=180°-60°=120°，
∴，
故答案为．
【点睛】本题主要考查扇形面积计算及正多边形的性质，熟练掌握扇形面积计算及正多边形的性质是解题的关键．
16. 如图是某风景区的一个圆拱形门，路面宽为，净高，则圆形拱门所在圆的半径为_____．
【答案】
【解析】
【分析】如图所示，连接，设⊙O的半径为r，则，利用垂径定理得到，再利用勾股定理建立方程，解方程即可得到答案．
【详解】解：如图所示，连接，设⊙O的半径为r，则，
∵，
∴，
由勾股定理，得：，即：，
解得，
∴圆拱形门所在圆的半径为，
故答案为：．
【点睛】本题主要考查了垂径定理，勾股定理，正确作出辅助线构造直角三角形是解题的关键．
17. 如图，在矩形中，点在边上，沿折叠矩形，使点落在边上的点处，若，，则的值为___.
【答案】##0.75
【解析】
【分析】此题考查了折叠的性质，矩形的性质以及三角函数的定义．解此题的关键是转化思想的应用．由四边形是矩形，可得：，，，由折叠的性质可得：，，由同角的余角相等，即可得，然后在中，即可求得答案．
【详解】解：∵四边形是矩形，
∴，，，
由题意得：，，
∴，，
∴，
∵在中，，，
∴，
∴．
故答案为．
18. 已知，当分别取，，，……，时，所对应值的总和是_____________.
【答案】
【解析】
【分析】本题考查了二次根式的化简求值、绝对值运算等知识点，掌握二次根式的化简方法是解题关键．先化简二次根式求出的表达式，再将的取值依次代入，然后求和即可得．
【详解】解：，
当时，，
当时，，
则所求的总和为：
故答案为：．
三、解答题：本大题共5小题，共26分．解答时，应写出必要的文字说明，证明过程或演算步骤．
19. 计算：．
【答案】
【解析】
【分析】原式根据算术平方根的意义，负整数指数幂，特殊角三角函数值以及绝对值的代数意义进行化简各项后，再进行加减运算即可得到答案．
【详解】解：
【点睛】此题主要考查了实数混合运算，熟练掌握运算法则是解答此题的关键．
20 先化简，再求值：，其中．
【答案】，
【解析】
【分析】本题主要考查了分式的化简求值，括号内先通分，再将除法转化为乘法，约分即可化简，再代入计算即可，熟练掌握分式的混合运算法则是解此题的关键．
【详解】解：
，
将代入得，原式．
21. 如图，已知锐角三角形，．
（1）尺规作图：
①作的垂直平分线l；
②作的平分线，且交于点M．
（2）若l与交于点P，，求的度数．
【答案】（1）①作图见解析，②作图见解析，（2）
【解析】
【分析】（1）①根据尺规作图作BC的垂直平分线l即可；②根据尺规作图作∠B的平分线BM即可；
（2）根据垂直平分线和角平分线的性质即可求解．
【详解】解：（1）①如图直线l为所求作的图形；②射线为所求作图形．
（2）∵BC的垂直平分线为l，
∴PB＝PC，
∴∠PBC＝∠PCB＝32°，
∵BM平分∠ABC，
∠ABP＝∠CBP＝32°，
∵∠A＝60°，
∴．
【点睛】本题考查了尺规作图、线段垂直平分线的性质、角平分线的性质，解决本题的关键是掌握尺规作图的方法和线段垂直平分线、角平分线的性质．
22. 永昌钟鼓楼位于甘肃省金昌市永昌县城中心．它是永昌历史文化的象征，是永昌的标志性建筑．整个建筑结构严谨、雄伟壮观，是河西走廊重要的古建筑之一．金昌市某校学生开展测量鼓楼高度的“数学综合与实践”活动，测量实践报告如下表：
根据上表中的测量方案及其数据，计算鼓楼的高度（结果保留整数）．
【答案】鼓楼的高度约为24米
【解析】
【分析】本题考查解直角三角形的应用-仰角俯角问题，利用正切定义分别求得，，然后利用列方程求解即可．
【详解】解：由题意，，
在中，，则，
在中，，则，
∴，
解得（米），
答：鼓楼的高度约为24米．
23. 为大力弘扬“奉献、友爱、互助、进步”的志愿精神，我市某社区开展了“文明新风进社区”系列志愿服务活动，参加活动的每位志愿者必须从A．“垃圾分类入户宣传”、B．“消防安全知识宣传”、C．“走访慰问孤寡老人”、D．“社区环境整治活动”四个活动主题中随机选取一个主题中随机选取一个主题．
（1）志愿者小李选取A．“垃圾分类入户宣传”这个主题的概率是 ．
（2）志愿者小张和小李从A、B、C、D四个主题中分别随机选取一个主题，请用列表或画树状图的方法，求他们选取相同主题的概率．
【答案】（1）；
（2）作图见解析，
【解析】
【分析】（1）直接根据概率公式求解即可；
（2）画树状图，共有16种等可能的结果，小张和小李选择相同主题的结果有4种，由概率公式求解即可．
【小问1详解】
解：由题意知志愿者小李选取A．“垃圾分类入户宣传”这个主题的概率是
故答案为：．
【小问2详解】
解：画树状图如图：
由图可知，共有16种等可能的结果，小张和小李选择相同主题的结果有共4种，可知小张和小李选择相同主题的概率为
∴小张和小李选择相同主题的概率为．
【点睛】本题考查了树状图求概率．解题的关键在于正确的列出所有情况．
四、解答题：本大题共5小题，共40分．解答时，应写出必要的文字说明，证明过程或演算步骤．
24. 为了落实“双减”政策，学校组织各种社团活动，丰富孩子们的课余生活．为了解该校全体学生参加该学校五个社团的意愿，随机抽取了名学生进行问卷调查，每人只能从中选择一个社团，现将问卷调查结果绘制成不完整的统计图表．

请你根据以上信息结合统计图解答下列问题：
（1）填空：______；______；扇形统计图中扇形B的圆心角是 度；
（2）请补全条形统计图；
（3）若该校有名学生，估计全校约有多少名学生愿意参加手工制作社团？
【答案】（1）12，10，108
（2）见解析 （3）960名
【解析】
【分析】本题考查扇形统计图和条形统计图的关联、用样本估计总体，看懂统计图并获取有用信息是解答的关键．
（1）先由乒乓球社团人数乘以其所占的百分比求得调查人数，再由调查人数乘以架子鼓社团的百分比可求得m值；由扇形统计图中其他社团的百分比可求得p值，由乘以架子鼓社团所占的百分比可求解圆心角的度数；
（2）先求得播音主持社团的人数，再补全条形统计图即可；
（3）用该校总人数乘以样本中参加手工制作社团的百分比即可求解．
【小问1详解】
解：调查人数为（名），（名），
，则，
扇形B的圆心角是，
故答案为：12，10，108；
【小问2详解】
解：（名），
补全条形统计图如图：
【小问3详解】
解：（名），
答：估计全校约有960名学生愿意参加手工制作社团．
25. 如图，一次函数的图象与反比例函数的图象交于，两点，与x轴交于点C，与y轴交于点D．
（1）求反比例函数与一次函数的表达式；
（2）若点P是y轴正半轴上一点，连接PA，PB，的面积是的面积的5倍，求点P的坐标．
【答案】（1）反比例函数的解析式为；一次函数的解析式为
（2）
【解析】
【分析】（1）把代入，求得，把代入，求得，得，把代入，求出的值即可；
（2）求出点的坐标，得出，根据列出关于的方程，求出的值即可
【小问1详解】
把代入，得，
∴
∴反比例函数的解析式为
把代入，得，
∴
把代入，得，
解得，
∴一次函数的解析式为
【小问2详解】
对于，令，则；，则
∴
∴
设，如图，
∵
∴
解得，
∴
【点睛】本题考查一次函数和反比例函数的交点问题，用待定系数法求一次函数的解析式，三角形的面积等知识点的综合运用，主要考查学生的计算能力和观察图形的能力，以及数形结合思想的运用．
26. 如图，在△ABC中，AB＝AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线EF，交AB和AC的延长线于E、F．
（1）求证：FE⊥AB；
（2）当AE＝6，sin∠CFD＝时，求EB的长．
【答案】（1）见解析；（2）.
【解析】
【分析】（1）先证明OD∥AB，得出∠ODF＝∠AEF，再由切线的性质得出∠ODF＝90°，证出∠AEF＝90°，即可得出结论；
（2）设OA＝OD＝OC＝r，先由三角函数求出AF，再证明△ODF∽△AEF，得出对应边成比例求出半径，得出AB，即可求出EB．
【详解】（1）证明：连接OD，如图所示：
∵OC＝OD，
∴∠OCD＝∠ODC，
∵AB＝AC，
∴∠ACB＝∠B，
∴∠ODC＝∠B，
∴OD∥AB，
∴∠ODF＝∠AEF，
∵EF与⊙O相切，
∴OD⊥EF，
∴∠ODF＝90°，
∴∠AEF＝∠ODF＝90°，
∴EF⊥AB；
（2）解：设OA＝OD＝OC＝r，
由（1）知：OD∥AB，OD⊥EF，
在Rt△AEF中，sin∠CFD＝，AE＝6，
∴AF＝10，
∵OD∥AB，
∴△ODF∽△AEF，
∴
∴
解得r＝，
∴AB＝AC＝2r＝，
∴EB＝AB﹣AE＝﹣6＝．
【点睛】本题考查了切线的性质、相似三角形的判定与性质以及解直角三角形；熟练掌握切线的性质，并能进行有关推理计算是解决问题的关键．
27. 【问题情境】
小睿遇到这样一个问题：如图1，在中，点D在线段上，，，，，求的长．
【问题探究】
小睿发现，过点C作，交的延长线于点E，经过推理和计算能够使问题得到解决，如图2．
（1）①的度数为______；②求的长；
【问题拓展】
（2）如图3，在四边形中，，，，与交于点E，，，求的长．
【答案】（1）①；②6；（2）
【解析】
【分析】本题主要考查了平行线的性质、相似三角形的判定和性质、解直角三角形等知识点，正确画出辅助线、构造直角三角形求解是解题的关键．
（1）①根据“两直线平行，同旁内角互补”即可解答；②通过证明得出，然后代入数据进行计算，再可得出，即可解答；
（2）过点D作于点F，先证明，得出，再证明，根据在中解直角三角形即可解答．
【详解】解：（1）①∵，，
∴，
∵，
∴，则；
故答案为：；
②∵，
∴，
∴，
∵，，
∴．
∴．
∵，
∴，
∴．
（2）解：过点D作于点F．
∵，
∴，
∴，
∴，
∵，，
∴．
在中，，
∴，
∴，
∴．
∵，
∴，
在中，，
∴，，
∴．
28. 如图，抛物线与轴交于A、B两点，与轴交于点C，直线过B、C两点，连接AC．
（1）求抛物线的解析式；
（2）求证：；
（3）点是抛物线上的一点，点D为抛物线上位于直线BC上方的一点，过点D作轴交直线BC于点E，点P为抛物线对称轴上一动点，当线段DE的长度最大时，求的最小值．
【答案】（1）；（2）见解析；（3）
【解析】
【分析】（1）先利用直线得到点B和点C的坐标，利用待定系数法求解；
（2）根据解析式求得点A的坐标，求出两个三角形的边长，根据两组对应边成比例夹角相等求证；
（3）设点D的坐标为，将线段DE的长用函数关系式表示为顶点式形式，利用函数的性质得到当时，线段DE的长度最大，得到点D的坐标，再利用轴对称及勾股定理求出答案即可．
【详解】（1）解：∵直线分别与轴和轴交于点B和点C，
∴点B的坐标为（4，0），点C的坐标为（0，2），
把，分别代入，
得，
解得，
∴抛物线的解析式为．
（2）∵抛物线与x轴交于点A，
∴，
解得，，
∴点A的坐标为，
∴，，
在中，，，
∴，
∴，
∵，
∴，
又∵，
∴．
（3）设点D的坐标为
则点E的坐标为
∴
=
∵，
∴当时，线段DE的长度最大．
此时，点D的坐标为，
∵，
∴点C和点M关于对称轴对称，
连接CD交对称轴于点P，此时最小．
连接CM交直线DE于点F，则，点F的坐标为，
∴，
∵
∴的最小值．
．
【点睛】此题考查的是二次函数的综合知识，利用待定系数法求函数解析式，函数图象与坐标轴的交点问题，函数的最值问题，轴对称的性质，勾股定理，证明两个三角形相似，熟练掌握各知识点是解题的关键．
活动课题
测量鼓楼高度
活动目的
运用三角函数知识解决实际问题
活动工具
测角仪、皮尺等测量工具
方案示意图
测量步骤
（1）利用测角仪站在B处测得城门楼最高点P的仰角为；
（2）前进了14米到达A处（点A，B，O在同一水平线上，测角仪高度忽略不计），在A处测得P点的仰角为．
测量数据
，，米
参考数据
，，，，，．
社团名称
A（乒乓球）
B（架子鼓）
C（手工制作）
D（播音主持）
E（舞蹈）
人数/人
4
m
16
n
4