2022-2023学年湖北省天门市九校八年级（下）期中数学试卷（含解析）

这是一份2022-2023学年湖北省天门市九校八年级（下）期中数学试卷（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.使二次根式 x+1有意义的x的取值范围是( )
A. x≠1B. x≥−1C. x≥1D. x≠−1
2.下列二次根式中，属于最简二次根式的是( )
A. 12B. 0.3C. 8D. 5
3.下列各式中，运算正确的是( )
A. 8− 3= 5B. 13× 27=9C. 3 2− 2=3D. 3× 5= 15
4.下列四组线段中，可以构成直角三角形的是( )
A. 1. 2, 3B. 4，5，6C. 6，8，11D. 5，12，23
5.等腰三角形的腰长为10，底长为12，则其底边上的高为( )
A. 13B. 8C. 25D. 64
6.下列四组条件中，不能判定四边形ABCD是平行四边形的是( )
A. AD=BC，AD//BCB. AD//BC，AB=DC
C. AD=BC，AB=DCD. AD//BC，AB//DC
7.菱形具有而一般平行四边形不具有的性质是( )
A. 两组对边分别相等B. 两组对角分别相等
C. 两条对角线互相平分D. 每一条对角线平分一组对角
8.如图，矩形ABCD的对角线AC，BD交于点O，AC=4cm，∠AOD=120°，则BC的长为cm．( )
A. 4 3B. 4C. 2 3D. 2
9.“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若ab=8，小正方形的面积为9，则大正方形的边长为( )
A. 9B. 6C. 5D. 4
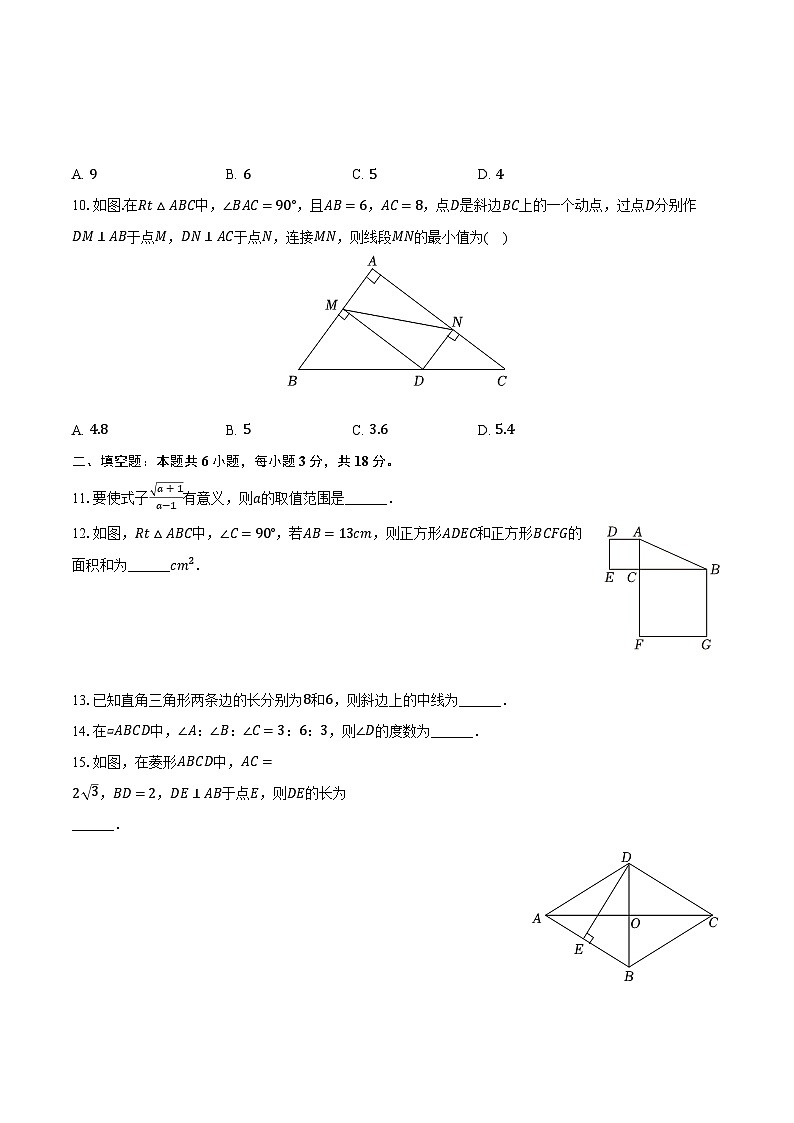
10.如图.在Rt△ABC中，∠BAC=90°，且AB=6，AC=8，点D是斜边BC上的一个动点，过点D分别作DM⊥AB于点M，DN⊥AC于点N，连接MN，则线段MN的最小值为( )
A. 4.8B. 5C. 3.6D. 5.4
二、填空题：本题共6小题，每小题3分，共18分。
11.要使式子 a+1a−1有意义，则a的取值范围是______．
12.如图，Rt△ABC中，∠C=90°，若AB=13cm，则正方形ADEC和正方形BCFG的面积和为______cm2．
13.已知直角三角形两条边的长分别为8和6，则斜边上的中线为______．
14.在▱ABCD中，∠A：∠B：∠C=3：6：3，则∠D的度数为______．
15.如图，在菱形ABCD中，AC=
2 3，BD=2，DE⊥AB于点E，则DE的长为
______．
16.如图，平行四边形ABCD中，对角线AC，BD相交于O，BD=2AD，E，F，G分别是OC，OD，AB的中点，下列结论：①BE⊥AC；②四边形BEFG是平行四边形；③EG=GF；④EA平分∠GEF.其中正确的是______．
三、解答题：本题共8小题，共60分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
(1)3 12−6 13+ 48；(2)2 27×53 23÷ 2．
18.(本小题6分)
在▱ABCD中，点E是AB的中点，请仅用无刻度的直尺分别在图1、图2中按要求作图(保留作图痕迹，不写作法)．

(1)在图1中，画出CD的中点F；
(2)在图2中，画出AD的中点G．
19.(本小题6分)
如图，在△ABC中，D为BC边上的一点，已知AB=13，AD=12，AC=15，BD=5，求CD的长．
20.(本小题6分)
如图，在▱ABCD中，E，F为对角线AC上的两点，且AE=CF，连接DE，BF，求证：DE/​/BF．
21.(本小题8分)
已知a=2+ 3，b=2− 3，求下列各式的值．
(1)a2−3ab+b2，(2)ba+ab．
22.(本小题8分)
如图，矩形ABCD中，AB=8，BC=4，过BD中点O的直线分别交AB、CD于点E、F．
(1)求证：四边形BEDF是平行四边形；
(2)当四边形BEDF是菱形时，求EB的长．
23.(本小题8分)
如图，在四边形ABCD中，AD//BC，AB=BC，对角线AC、BD交于点O，BD平分∠ABC，过点D作DE⊥BC，交BC的延长线于点E，连接OE．
(1)求证：四边形ABCD是菱形；
(2)若DC=2 5，AC=4，求OE的长．
24.(本小题10分)
矩形ABCD中，AB=6，AD=8，E是BC边上一点，EF⊥AE且EF=AE．

(1)如图1，当F在CD边上时，求BE的长；
(2)如图2，过点F作FH⊥CD于H，若FH=1，求BE的长；
(3)如图3，若DF⊥EF，请直接写出BE的长．
答案和解析
1.【答案】B
【解析】解：由题意得，x+1≥0，
解得x≥−1．
故选：B．
根据被开方数大于等于0列式计算即可得解．
本题考查的知识点为：二次根式的被开方数是非负数．
2.【答案】D
【解析】解： 12= 22，被开方数含分母，不是最简二次根式；
0.3= 3010，被开方数含分母，不是最简二次根式；
8=2 2，被开方数中含能开得尽方的因数，不是最简二次根式；
5是最简二次根式，
故选：D．
根据最简二次根式的条件进行判断即可．
本题考查的是最简二次根式的概念，最简二次根式的条件：(1)被开方数的因数是整数或字母，因式是整式；(2)被开方数中不含有可化为平方数或平方式的因数或因式．
3.【答案】D
【解析】解：A． 8=2 2，与 3不是同类二次根式，不能进行加减运算，此选项错误；
B. 13× 27= 13×27= 9=3，此选项计算错误；
C.3 2− 2=2 2，此选项错误；
D. 3× 5= 3×5= 15，此选项计算正确；
故选：D．
根据二次根式的加减、乘法运算法则计算可得答案．
本题主要考查二次根式的混合运算，解题的关键是掌握二次根式的加减运算和乘法运算法则．
4.【答案】A
【解析】解：A、12+( 2)2=( 3)2，能构成直角三角形，故此选项符合题意；
B、42+52≠62，不能构成直角三角形，故此选项不合题意；
C、62+82≠112，不能构成直角三角形，故此选项不合题意；
D、52+122≠232，不能构成直角三角形，故此选项不符合题意；
故选：A．
利用勾股定理逆定理进行计算即可．
此题主要考查了勾股定理逆定理，关键是掌握勾股定理的逆定理将数转化为形，作用是判断一个三角形是不是直角三角形．必须满足较小两边平方的和等于最大边的平方才能做出判断．
5.【答案】B
【解析】解：作底边上的高并设此高的长度为x，根据勾股定理得：62+x2=102，
解得：x=8．
故选：B．
先作底边上的高，由等腰三角形的性质和勾股定理即可求出此高的长度．
本题考点：等腰三角形底边上高的性质和勾股定理，等腰三角形底边上的高所在直线为底边的中垂线．然后根据勾股定理即可求出底边上高的长度．
6.【答案】B
【解析】解：A、根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD为平行四边形，故此选项不合题意；
B、不能判定四边形ABCD是平行四边形，故此选项符合题意；
C、根据两组对边分别相等的四边形是平行四边形可判定四边形ABCD为平行四边形，故此选项不合题意；
D、根据两组对边分别平行的四边形是平行四边形可判定四边形ABCD为平行四边形，故此选项不合题意；
故选：B．
根据平行四边形的判定定理分别进行分析判断即可．
此题主要考查了平行四边形的判定，解题的关键是掌握(1)两组对边分别平行的四边形是平行四边形．(2)两组对边分别相等的四边形是平行四边形．(3)一组对边平行且相等的四边形是平行四边形．(4)两组对角分别相等的四边形是平行四边形．(5)对角线互相平分的四边形是平行四边形．
7.【答案】D
【解析】解：由菱形性质可知，每一条对角线平分一组对角；
而平行四边形不具备这样的性质；
其他A，B，C均是菱形和平行四边形共有的性质．
故选：D．
菱形的对角线垂直和每一条对角线平分一组对角是菱形的重要性质，而平行四边形不具备这样的性质．
本题主要考查菱形的性质，熟练掌握菱形的性质特点是解答本题的关键．
8.【答案】C
【解析】解：∵矩形ABCD的对角线AC，BD交于点O，AC=4cm，
∴OA=OB=12AC=2cm．
又∵∠AOD=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴AB=OA=OB=2cm．
∴在直角△ABC中，∠ABC=90°，AB=2cm，AC=4cm，
∴BC= AC2−AB2= 42−22=2 3(cm)．
故选：C．
利用矩形对角线的性质得到OA=OB.结合∠AOD=120°知道∠AOB=60°，则△AOB是等边三角形；最后在直角△ABC中，利用勾股定理来求BC的长度即可．
本题考查了矩形的性质和等边三角形的性质和判定的应用，勾股定理，解此题的关键是求出OA、OB的长，题目比较典型，是一道比较好的题目．
9.【答案】C
【解析】解：由题意可知：中间小正方形的边长为：a−b，
∵每一个直角三角形的面积为：12ab=12×8=4，
∴大正方形的面积为：4×12ab+(a−b)2=16+9=25，
∴大正方形的边长为5．
故选：C．
由题意可知：中间小正方形的边长为：a−b，根据勾股定理以及题目给出的已知数据即可求出大正方形的边长．
本题考查勾股定理的证明，解题的关键是熟练运用勾股定理以及完全平方公式，本题属于基础题型．
10.【答案】A
【解析】解：∵∠BAC=90°，且AB=6，AC=8，
∴BC= BA2+AC2= 62+82=10，
∵DM⊥AB，DN⊥AC，
∴∠DMA=∠DNA=∠BAC=90°，
∴四边形DMAN是矩形，
∴MN=AD，
∴当AD⊥BC时，AD的值最小，
此时，S△ABC=12AB⋅AC=12BC⋅AD，
∴AD=AB⋅ACBC=6×810=4.8，
∴MN的最小值为4.8，
故选：A．
由勾股定理求出BC的长，再证明四边形DMAN是矩形，可得MN=AD，根据垂线段最短和三角形面积即可解决问题．
本题主要考查了矩形的判定和性质、勾股定理、三角形面积、垂线段最短等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
11.【答案】a≥−1且a≠1
【解析】解：由题意，得
a+1≥0，a−1≠0，
解得a≥−1且a≠1，
故答案为：a≥−1且a≠1．
根据分子的被开方数不能为负数，分母不能为零，可得答案．
本题考查了分式有意义的条件，利用分子的被开方数不能为负数，分母不能为零得出不等式是解题关键．
12.【答案】169
【解析】解：在Rt△ACB中，由勾股定理得：AC2+BC2=AB2=132=169(cm2)，
∴正方形ADEC和正方形BCFG的面积和=AC2+BC2=169cm2，
故答案为：169．
由勾股定理得AC2+BC2=AB2=132=169(cm2)，再由正方形的面积公式即可得出结论．
本题考查了勾股定理以及正方形的性质，熟练掌握勾股定理是解题的关键．
13.【答案】4或5
【解析】解：(1)若8为直角三角形的斜边时，根据直角三角形的性质斜边上的中线等于斜边的一半，斜边上的中线为12×8=4；
(2)若8为直角三角形的直角边时，根据勾股定理斜边= 82+62=10，根据直角三角形的性质斜边上的中线等于斜边的一半，斜边上的中线为12×10=5．
∴斜边上的中线为4或5．
本题利用直角三角形的性质及勾股定理解答即可．分两种情况．
解答此题时要注意分8为直角边和斜边两种情况讨论，不要漏解．
14.【答案】120°
【解析】解：如图，∵四边形ABCD是平行四边形，
∴∠A=∠C，∠B=∠D，∠A+∠B=180°，
∵∠A：∠B=3：6，
∴∠B=69×180°=120°，
∴∠D=∠B=120°．
故答案为：120°．
由平行四边形的对角相等、邻角互补，结合已知条件求出∠B=120°，即可得出答案．
此题考查了平行四边形的性质．熟记平行四边形的对角相等、邻角互补是解题的关键．
15.【答案】 3
【解析】解：∵四边形ABCD是菱形，AC=2 3，BD=2，
∴AO=CO=12AC= 3，BO=DO=12BD=1，AC⊥BD，
∴∠AOB=90°，
∴AB= AO2+BO2=2，
∴S菱形ABCD=DE·AB=12AC·BD，
∴DE=12×2 3×22= 3．
故答案为： 3．
由菱形的性质可得AO=CO=12AC= 3，BO=DO=12BD=1，AC⊥BD，由勾股定理可求AB的长，由菱形的面积公式可求解．
本题考查了菱形的性质，勾股定理，掌握菱形的面积公式是解题的关键．
16.【答案】①②④
【解析】解：∵四边形ABCD是平行四边形，
∴BO=DO=12BD，AD=BC，AB=CD，AB/​/BC，
又∵BD=2AD，
∴OB=BC=OD=DA，且点E是OC中点，
∴BE⊥AC，
故①正确，
∵E、F分别是OC、OD的中点，
∴EF/​/CD，EF=12CD，
∵点G是Rt△ABE斜边AB上的中点，
∴GE=12AB=AG=BG，
∴EG=EF=AG=BG，无法证明GE=GF，
故③错误，
∵BG=EF，BG//EF//CD，
∴四边形BEFG是平行四边形，
故②正确，
∵EF/​/CD/​/AB，
∴∠BAC=∠ACD=∠AEF，
∵AG=GE，
∴∠GAE=∠AEG，
∴∠AEG=∠AEF，
∴AE平分∠GEF，
故答案为：①②④．
由平行四边形的性质可得OB=BC，由等腰三角形的性质可判断①正确，由直角三角形的性质和三角形中位线定理可判断③错误，由BG=EF，BG//EF//CD可证四边形BEFG是平行四边形，可得②正确．由平行线的性质和等腰三角形的性质可判断④正确．
本题考查了菱形的判定，平行四边形的性质，全等三角形的判定和性质，三角形中位线定理等知识，灵活运用相关的性质定理、综合运用知识是解题的关键．
17.【答案】解：(1)3 12−6 13+ 48
=3×2 3−6× 33+4 3
=6 3−2 3+4 3
=8 3．
(2)2 27×53 23÷ 2
=2×3 3×53× 63× 22
=10．
【解析】(1)根据二次根式加减法的运算法则计算即可．
(2)根据二次根式乘除法的运算法则计算即可．
本题考查二次根式的混合运算，熟练掌握运算法则是解答本题的关键．
18.【答案】解：(1)如图1，点F为所作；
(2)如图2，点G为所作．

【解析】(1)连接AC、BD，它们相交于点O，连接EO并延长EO交CD于F点，则利用平行四边形的中心对称性得到F点为CD的中点；
(2)由(1)得到F点，连接BF、CE，它们相交于点Q，延长QO交AD于G点．
本题考查了作图−复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了平行四边形的性质．
19.【答案】解：∵AB=13，AD=12，BD=5，
∴AB2=AD2+BD2，
∴△ADB是直角三角形，∠ADB=90°，
∴△ADC是直角三角形，
在Rt△ADC中，CD= AC2−AD2= 152−122=9．
【解析】本题考查了勾股定理及勾股定理的逆定理，属于基础题，解答本题的关键是判断出∠ADB=90°．
根据勾股定理的逆定理可判断出△ADB为直角三角形，即∠ADB=90°，在Rt△ADC中利用勾股定理可得出CD的长度．
20.【答案】证明：∵四边形ABCD是平行四边形，
∴DC=AB，DC/​/AB，
∴∠CAB=∠DCA，
∵AE=CD，
∴AF=CE，
在△DEC和△BFA中
DC=AB∠DCA=∠CABAF=CE，
∴△DEC≌△BFA(SAS)，
∴∠DEF=∠BFA，
∴DE/​/BF．
【解析】直接利用平行四边形的性质可得DC=AB，DC/​/AB，进而可证出∠CAB=∠DCA，然后再证明△DEC≌△BFA(SAS)，可得∠DEF=∠BFA，然后可根据内错角相等两直线平行得到结论．
此题主要考查了平行四边形的性质，关键是正确证明△DEC≌△BFA，此题难度不大．
21.【答案】解：∵a=2+ 3，b=2− 3，
∴a+b=4，a−b=2 3，ab=4−3=1
(1)a2−3ab+b2
=(a−b)2−ab
=4×3−1
=11；
(2)ba+ab
=(a+b)2ab−2
=421−2
=14．
【解析】(1)根据完全平方公式列出等式，即a2−3ab+b2=(a−b)2−ab，再整体代入计算即可；
(2)根据完全平方公式列出等式，即ba+ab=(a+b)2ab−2，再整体代入计算即可；
本题考查的是二次根式的化简求值和分式的加减法，熟练掌握其运算法则是解题的关键．
22.【答案】(1)证明：∵矩形ABCD
∴AB/​/CD
∴∠FDO=∠EBO，
在△DOF和△BOE中
∠FDO=∠EBOOD=OB∠DOF=∠BOE，
∴△DOF≌△BOE(ASA)
∴DF=BE，
又∵DF/​/BE
∴四边形BEDF是平行四边形；
(2)∵四边形BEDF是菱形
∴DE=BE，
∵矩形ABCD
∴∠A=90°，AD=BC=4
∴AD2+AE2=DE2
∴16+(8−BE)2=BE2，
∴BE=5．
【解析】(1)根据平行四边形ABCD的性质，判定△BOE≌△DOF(ASA)，得出四边形BEDF的对角线互相平分，进而得出结论；
(2)在Rt△ADE中，由勾股定理得出方程，解方程求出BE即可．
本题主要考查了矩形的性质，菱形的性质、勾股定理、全等三角形的判定与性质，熟练掌握矩形的性质和勾股定理，证明三角形全等是解决问的关键．
23.【答案】(1)证明：∵AD/​/BC，
∴∠ADB=∠CBD，
∵BD平分∠ABC，
∴∠ABD=∠CBD，
∴∠ADB=∠ABD，
∴AD=AB，
∵AB=BC，
∴AD=BC，
∵AD/​/BC，
∴四边形ABCD是平行四边形，
又∵AB=BC，
∴四边形ABCD是菱形；
(2)解：∵四边形ABCD是菱形，
∴AC⊥BD，OB=OD，OA=OC=12AC=2，
在Rt△OCD中，由勾股定理得：OD= CD2−OC2=4，
∴BD=2OD=8，
∵DE⊥BC，
∴∠DEB=90°，
∵OB=OD，
∴OE=12BD=4．
【解析】(1)由平行线的性质和角平分线得出∠ADB=∠ABD，证出AD=AB，由AB=BC得出AD=BC，即可得出结论；
(2)由菱形的性质得出AC⊥BD，OB=OD，OA=OC=12AC=2，在Rt△OCD中，由勾股定理得OD=4，得出BD=2OD=8，再由直角三角形斜边上的中线性质即可得出结果．
本题考查了菱形的判定与性质、平行四边形的判定、等腰三角形的判定、平行线的性质、勾股定理、直角三角形斜边上的中线性质；熟练掌握菱形的判定与性质是解题的关键．
24.【答案】解：(1)在矩形ABCD中，∠B=∠C=90°，BC=AD=8，CD=AB=6，
∴∠BAE+∠AEB=90°，
∴EF⊥AE，
∴∠AEF=90°
∴∠AEB+∠CEF=90°，
∴∠BAE=∠CEF，
在△ABE和△ECF中，
∠B=∠C∠BAE=∠CEFAE=EF，
∴△ABE≌△ECF(AAS)，
∴CE=AB=6，
∴BE=BC−CE=8−6=2；
(2)如图2，过点F作FM⊥BC于M，

∵四边形ABCD是矩形，
∴∠BCD=90°，
∴∠MCH=90°，
∵FH⊥CD，
∴∠CHF=90°，
∴∠M=∠CHF=∠MCH=90°，
∴四边形MCHF是矩形，
∴CM=FH=1，
由(1)同理得：△ABE≌△EMF(AAS)，
∴ME=AB=6，
∴CE=6−1=5，
∴BE=8−5=3；
(3)如图3，延长EC，DF交于点P，

∵DF⊥EF，EF⊥AE，
∴AE/​/DF，
在矩形ABCD中，AD//BC，
∴四边形AEPD是平行四边形，
∴PE=AD=8，
∴S▱AEPD=PE⋅CD=AE⋅EF，即8×6=AE2，
∴AE2=48，
在Rt△ABE中，BE= AE2−AB2= 48−36=2 3．
【解析】(1)通过AAS证明△ABE≌△ECF，可得CE=AB=6即可求出BE的长；
(2)如图2，过点F作FM⊥BC于M，先证明CM=FH=1，由(1)同理得：△ABE≌△EMF(AAS)，即可解决问题；
(3)延长EC，DF交于点P，先证得四边形AEPD是平行四边形，则有S▱AEPD=PE⋅CD=AE⋅EF，即8×6=AE2，在Rt△ABE中，勾股定理求出BE，即可解决问题．
本题是四边形的综合题，主要考查了矩形的性质，平行四边形的性质和判定，三角形全等的判定与性质，勾股定理等知识，作辅助线构造出全等三角形是解题的关键．