江苏省兴化市常青藤学校联盟2023-2024学年八年级下册第1次月考数学试题（含解析）

这是一份江苏省兴化市常青藤学校联盟2023-2024学年八年级下册第1次月考数学试题（含解析），共22页。试卷主要包含了若使分式有意义，则的取值范围是，我们都知道，四边形具有不稳定性，约分等内容，欢迎下载使用。

八年级数学试题
（考试时间：120分钟，满分：150分）
请注意：1．本试卷分选择题和非选择题两个部分
2．所有试题的答案均填写在答题卡上，答案写在试卷上无效．
3．作图必须用2B铅笔，并请加黑加粗．
第一部分 选择题（共18分）
一．选择题（本大题共有6小题，每小题3分，共18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）
1．下列图形中，属于中心对称图形的是（ ）
A． B．
C． D．
2．“数学课本共154页，某同学随手翻开，恰好翻到第88页”，这个事件是（ ）
A．必然事件B．不可能事件C．随机事件D．以上都不正确
3．为了调查某校学生中午是否在校就餐情况，在全校的2400名学生中随机抽取了100名学生，下列说法正确的是（ ）
A．此次调查属于全面调查 B．2400名学生是总体
C．样本容量是100 D．被抽取的每一名学生称为个体
4．若分式中的和都扩大为原来的3倍后，分式的值不变，则A可能是（ ）
A．B．C．D．3
5．若使分式有意义，则的取值范围是（ ）
A．B．C．D．
6．我们都知道，四边形具有不稳定性．老师制作了一个正方形教具用于课堂教学，数学课代表小亮在取道具时不小心使教具发生了形变（如图），若正方形道具边长为，，则四边形的面积减少了（ ）
A．B．C．D．
第二部分 非选择题部分（共132分）
二．填空题（本大题共10小题，每小题3分，满分30分．请把答案直接填写在答题卡相应位置上．）
7．要反映兰州市一周大气中的变化情况，宜采用 （填“条形”或“折线”或“扇形”） ．
8．某班在5名男生和3名女生中，随机选取1名学生作为学生代表，则选中 生的可能性较大．（填“男”或“女”）
9．约分： .
10．如图，在▱ABCD中，对角线AC，BD交于点O，若AO＝3，则AC＝ ．
11．用反证法证明“已知，．求证：”．第一步应先假设 ．
12．若菱形的两条对角线长分别是6cm，8cm，则该菱形的面积是 cm2．
13．如图，正方形ABCD的边长为1，点E在BC的延长线上．如果BE=BD，那么CE=
14．若，则的值为 ．
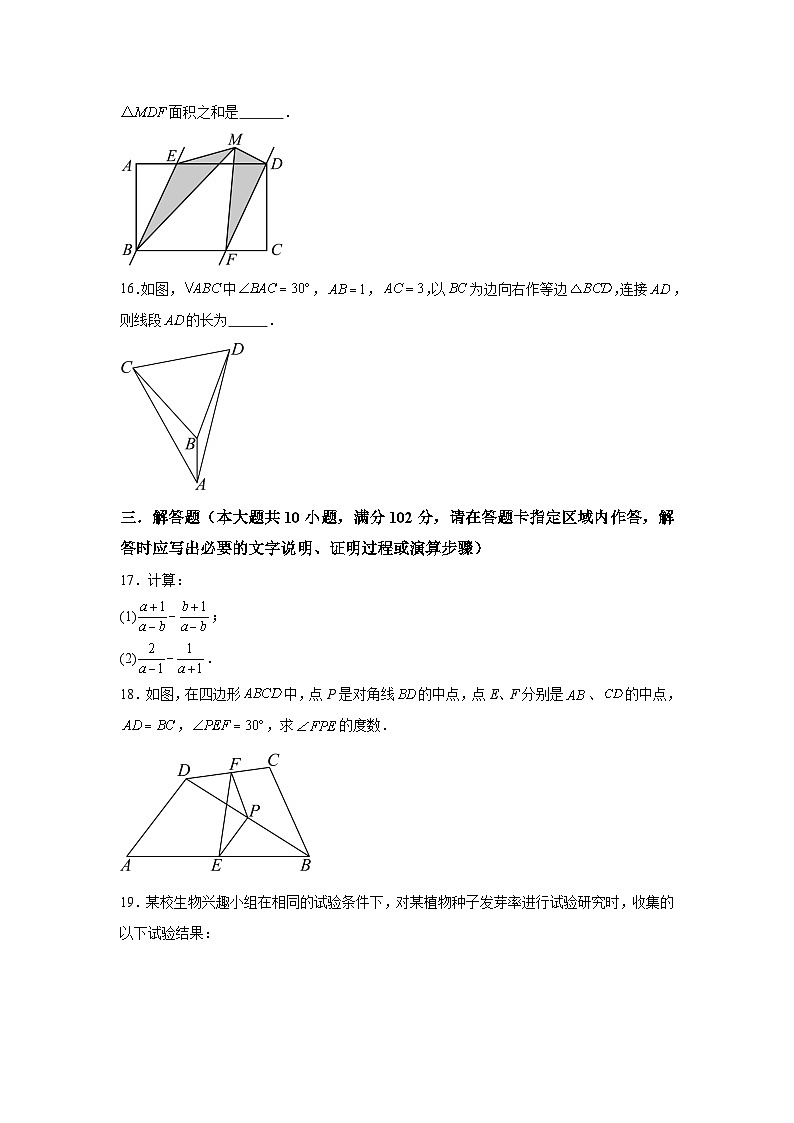
15．如图，在矩形中，，点E、F分别在边上，，点M为直线之间一点，连接，则与面积之和是 ．

16．如图，中，，，以为边向右作等边，连接，则线段的长为 ．
三．解答题（本大题共10小题，满分102分，请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）
17．计算：
(1)；
(2)．
18．如图，在四边形中，点P是对角线的中点，点E、F分别是、的中点，，，求的度数．

19．某校生物兴趣小组在相同的试验条件下，对某植物种子发芽率进行试验研究时，收集的以下试验结果：
(1)求表中的值；
(2)任取一粒这种植物的种子，请你估计它能发芽的概率（精确到）；
(3)若该学校劳动基地需要这种植物幼苗株，试估算该小组需要准备多少粒种子进行发芽培育．
20．我校为丰富课后托管服务，增设了“阅读广角”、“魅力足球”、“心动音乐”、“思维课堂”四个兴趣班，要求每名学生从中选择一个进行报名，经报名后，学校随机抽取了部分学生进行抽样调查，根据调查结果，绘制了如下两幅统计图：
根据以上信息回答下列问题：
(1)本次抽样调查的样本容量为 ，在扇形统计图中，“心动音乐”对应的圆心角的大小是 ．
(2)补全条形统计图．
(3)若我校有名学生，请估计全校选择“思维课堂”的学生人数，
21．如图，在中，对角线，交于点，．
(1)求证：四边形是矩形；
(2)若，，作的平分线交于点，求的长．
22．如图，已知菱形．请按要求在图中仅用无刻度的直尺画图．
(1)在图1中，点E是的中点，画出线段的中点M；

(2)在图2中，，垂足为E，过点C画出边上的高．

23．在边长为1个单位长度的小正方形组成的网格中，建立如图所示的平面直角坐标系是格点三角形（顶点在网格线的交点上）；
(1)作出关于原点O成中心对称的，并写出三个顶点坐标（_____），（______），（______）；
(2)把向上平移4个单位长度得到，画出；
(3)与成中心对称，请直接写出对称中心的坐标（________）．
24．【定理重现】如图是某数学教材中的部分内容．
（1）请根据教材中的分析和图①．写出“平行四边形的对角线互相平分”这一性质定理的证明过程：
【性质应用】
（2）如图②，的对角线相交于点，过点且与分别相交于点，连接．求证：四边形是平行四边形；
25．已知：，．
(1)当时，计算的值；
(2)当时，判断与的大小关系，并说明理由；
(3)设，若均为非零整数，求的值．
26．阅读下面材料：
我遇到这样一个问题：如图1，在正方形中，点E、F分别为、边上的点，，连接，求证：．我是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段集中到同一条线段上．他先后尝试了平移、翻折、旋转的方法，发现通过旋转可以解决此问题．他的方法是将绕点A顺时针旋转得到（如图2），此时即是．
请回答：在图2中，的度数是 ．
参考我得到的结论和思考问题的方法，解决下列问题：
（1）如图3，在直角梯形中，，，，E是上一点，若，，求的长度．
（2）如图4，中，，，以为边作正方形，连接．当 时，线段有最大值，并求出的最大值．
参考答案与解析
1．B
【分析】根据中心对称图形的定义进行逐一判断即可：把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．
【解答】解：把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．
由定义可判定A、C、D选项的图形不是中心对称图形，故不符合题意；
B选项的图形是中心对称图形，符合题意．
故选：B．
【点拨】本题主要考查了中心对称图形，熟知中心对称图形的定义是解题的关键．
2．C
【分析】本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
根据事件发生的可能性大小判断．
【解答】解：“数学课本共154页，某同学随手翻开，恰好翻到第88页”，这个事件是随机事件，
故选：C．
3．C
【分析】此题主要考查了总体、个体、样本．正确理解总体、个体、样本的概念是解决本题的关键．总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体．
【解答】解：A、此次调查属于抽样调查，故此选项不合题意；
B、2400名学生中午是否在校就餐情况是总体，故此选项不合题意；
C、样本容量是100，故此选项符合题意；
D、被抽取的每一名学生中午是否在校就餐情况称为个体，故此选项不合题意．
故选：C．
4．A
【分析】根据分式的性质即可求解．
【解答】解：和都扩大为原来的3倍得到：
因为分式的值不变
所以是同时含有和的一次二项式
故选：A
【点拨】本题考查分式的性质．掌握相关性质是解题的关键．
5．A
【分析】本题考查了分式有意义的条件．从以下三个方面透彻理解分式的概念：（1）分式无意义分母为零；（2）分式有意义分母不为零；（3）分式值为零分子为零且分母不为零．分母不为零，分式有意义可得，再解即可．
【解答】解：当分母，即时，分式有意义，
故选：A．
6．A
【分析】本题考查了正方形的性质，菱形的判定与性质，直角三角形的性质．
过点作交延长线于E，先证明四边形是菱形，得，则，利用直角三角形的性质得求得，然后用正方形的面积减去菱形的面积即可．
【解答】解：过点作交延长线于E，如图，
∵正方形，
∴
∴
∴四边形是菱形，
∴
∴
∵
∴
∴
∴四边形的面积减少了，
故选：A．
7．折线
【分析】根据统计图的特点进行分析可得：扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；折线统计图表示的是事物的变化情况；条形统计图能清楚地表示出每个项目的具体数目．
【解答】解：要反映某市一周大气中PM2.5的变化情况，宜采用 折线统计图，
故答案为：折线．
【点拨】本题考查了统计图的选择，掌握扇形统计图、折线统计图、条形统计图各自的特点是解题的关键．
8．男
【分析】根据题意，求出男生和女生当选的概率，再进行比较即可解答．
【解答】解：共有5名男生和3名女生，随机抽签，
抽到男生的概率是，抽到女生的概率是，
选中男生的可能性较大，
故答案为：男．
【点拨】此题考查了概率的应用，解题的关键是掌握概率的公式：有n种等可能的结果，事件A包含其中的k种结果，那么事件A发生的概率为．
9．
【分析】根据分式的约分解答本题即可．
【解答】解：=，
故答案为：．
【点拨】本题考查了约分，解答本题的关键是明确约分的方法．
10．6
【分析】根据平行四边形的性质，可得，结合题意即可求得．
【解答】四边形是平行四边形，
，
，
．
故答案为：．
【点拨】本题考查了平行四边形的性质，理解平行四边形的性质是解题的关键．
11．
【分析】用反证法证明问题的关键是清楚结论的反面是什么，写出与条件相反的假设即可
【解答】解： “已知，．求证：”．第一步应先假设．
故答案为：．
【点拨】本题考查的是反证法的应用，解题的关键是要懂得反证法的意义及步骤．在假设结论不成立时，要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．
12．24
【分析】已知对角线的长度，根据菱形的面积计算公式即可计算菱形的面积．
【解答】解：该菱形的面积是S=ab=×6×8=24cm2，
故答案为：24．
【点拨】本题考查了菱形的面积计算公式，解题的关键是牢记公式．
13．
【分析】由正方形的性质可知BC=CD=1，再由勾股定理求BD，从而可求解．
【解答】解：∵四边形ABCD为正方形，
∴BC=CD=1，
由勾股定理，得，
∴CE=BE-BC=BD-BC=．
故答案为：．
【点拨】本题考查了正方形的性质，及勾股定理的运用．关键是熟练掌握相关的性质是解题的关键．
14．1
【分析】将已知条件变形，然后整体代入求解即可．
【解答】解：∵，
∴，
∴，
故答案为：1．
【点拨】题目主要考查求代数式的值，利用整体法求解是解题关键．
15．8
【分析】先根据矩形的性质和已知条件证明四边形是平行四边形，则可求平行四边形的面积，再根据、的高的和等于点D直线距离，则与面积之和等于平行四边形的面积的一半，据此解答即可．
【解答】解：∵矩形中，，
∴,
∵
∴,
∴,
∴四边形是平行四边形，
∴平行四边形的面积为
∵、的高的和等于点D直线距离，
∴与面积之和等于平行四边形的面积的一半，
∴与面积之和是8．
故答案为8．
【点拨】本题主要考查了矩形的性质、平行四边形的判定与性质、三角形的面积等知识点，明确与面积之和等于平行四边形的面积的一半是解答本题的关键．
16．
【分析】本题考查了全等三角形的判定与性质，勾股定理，等边三角形的性质，以为边作等边三角形，连接，先证明，得，再在中，根据勾股定理即可．
【解答】解：如图以为边作等边三角形，连接，
，
，
在等边中，，，
，即，
，
，
在中，，
故答案为：．
17．(1)；
(2)．
【分析】本题考查了分式的加减，掌握运算法则是解题的关键．
（1）根据分式的加减运算法则进行计算即可；
（2）根据分式的加减运算法则进行计算即可．
【解答】（1）解：
．
（2）解：
．
18．
【分析】根据中位线的性质得出，，根据，得出，根据等腰三角形的性质得出，根据三角形内角和得出求出．
【解答】解：∵P是的中点，E，F分别是、的中点，
∴，分别是与的中位线，
∴，，
又∵，
∴，
∴，
∴．
【点拨】本题主要考查了中位线的性质，三角形内角和定理的应用，等腰三角形的性质，解题的关键是熟练掌握三角形的中位线等于第三边的一半．
19．(1)，；
(2)任取一粒这种植物的种子，估计它能发芽的概率是；
(3)估算至少需要准备粒种子进行发芽培育．
【分析】本题主要考查利用频率估计概率，大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．
（1）用发芽种子数除以试验的种子数即可得出的值；
（2）根据频率估计概率求解即可；
（3）用需要这种植物幼苗数量除以种子能发芽的概率可得答案．
【解答】（1）解：，
，
∴，．
（2）解：概率是大量重复试验的情况下，频率的稳定值可以作为概率的估计值，即次数越多的频率越接近于概率，
∴任取一粒这种植物的种子，估计它能发芽的概率是．
（3）解：
∴估算至少需要准备粒种子进行发芽培育．
20．(1)50，；
(2)补全图形见解析
(3)480人
【分析】本题考查了扇形统计图与条形统计图、用样本评估总体、求扇形统计图的圆心角及画条形统计图：
（1）利用“频数÷百分比=总体”可求得本次抽样调查的样本容量，再利用乘“心动音乐”对应的百分比即可求解；
（2）根据总体乘百分比等于频数可求得“阅读广角”的人数，再补全条形统计图即可；
（3）用样本评估总体的方法即可求解；
理解题意，能从统计图中获取相关信息是解题的关键．
【解答】（1）解：（人），
∴本次抽样调查的样本容量为50，
，
∴“心动音乐”对应的圆心角的大小是，
故答案为：50，．
（2）“阅读广角”的人数为：（人），
补全条形统计图如下：
（3）（人），
答：全校3000名学生中，选择“思维课堂”的学生大约有480人．
21．(1)见解析
(2)
【分析】本题考查了矩形的判定和性质，勾股定理，角平分线的定义，熟练掌握矩形的判定和性质定理是解题的关键．（1）根据平行四边形的性质得到，，根据矩形的判定定理即可得到结论；（2）如图，根据矩形的性质得到，，根据角平分线的定义得到，根据勾股定理得到，根据直角三角形的性质即可得到结论．
【解答】（1）证明：四边形是平行四边形，
，．
，
，
平行四边形为矩形；
（2）如图，
四边形是矩形，
，．
为的平分线，
．
，，，
，
，
，，
，
．
22．(1)见解析
(2)见解析
【分析】（1）如图，连接，则，的交点为三条中线的交点，连接并延长交于即可；
（2）如图，连接交于，连接并延长交于，连接即可．
【解答】（1）解：如图1，点M即为所求；
．
（2）如图2，即为所求．
．
【点拨】本题考查的是三角形的中线的性质，菱形的性质，直角三角形斜边上的中线等于斜边的一半，矩形的判定与性质，熟练的利用基本几何图形的性质进行作图是解本题的关键．
23．(1)作图见解析；；；
(2)见解析
(3)
【分析】此题考查中心对称图形的画法，平移图形的画法，中心对称的性质及平移的性质，对称中心的确定方法，正确掌握中心对称的性质及平移的性质是解题的关键.
（1）根据中心对称的性质作出点A、B、C的对应点，，，然后顺次连接即可；
（2）根据平移特点先作出点，，平移后的对应点，，，然后顺次连接即可；
（3）连接两组对称点的交点即为对称中心，然后根据中点坐标公式求出此点的坐标即可．
【解答】（1）解：如图，为所求作的三角形；
根据图可知，，，．
故答案为：；；．
（2）解：如图，为所求作的三角形；
（3）解：连接、，则、的交点即为对称中心，
∵，，
∴对称中心的坐标为，
即对称中心的坐标为．
故答案为：．
24．（1）见解析，（2）见解析．
【分析】此题考查了平行四边形的判定和性质，全等三角形的判定与性质，解题的关键是掌握平行四边形的判定和性质．
（1）先判断出，进而判断出，即可得出结论；
（2）根据平行四边形的性质和全等三角形的判定和性质解答即可．
【解答】证明：（1）∵四边形是平行四边形，
∴，
∴，，
∴，
∴；
（2）∵四边形是平行四边形，
∴，
∴，，
∴，
∴，
∴四边形是平行四边形．
25．(1)的值为；
(2)，理由见解析；
(3)的值为或．
【分析】本题考查分式运算和比较大小， 正确进行分式的加减运算是求解本题的关键．
（1）将代入计算的值即可；
（2）先求差，再比较差与的大小关系；
（3）先表示，再求的整数值，进而可以解决问题．
【解答】（1）解：当时，
，
∴的值为．
（2）解：当时，理由如下：
∵
或
∴当 且时，，
当时，，
∴当时，．
（3）解：∵，，
∴，
∵均为非零整数，
时，则；
时，则；
时，则；
时，则；
综上所述：的值为或．
26．阅读材料：；（1）；（2），
【分析】阅读材料：根据旋转的性质可得，再求出，然后根据计算即可得解；
（1）过点作交的延长线于点，可得四边形是正方形，再设，根据上面的结论表示出，再求出、，然后在中，利用勾股定理列式进行计算即可得解；
（2）过点作，取，连接，由勾股定理可求的长，再证出，则线段有最大值时，只需最大即可，从而可得当三点共线时，取最大值，由此求解即可得．
【解答】解：阅读材料：由旋转的性质可知，，
∴，，
∵四边形是正方形，
∴，
∵，
，即，
故答案为：；
（1）如图，点作交的延长线于点，
∵，，
∴，
∵，
∴四边形是正方形，
∴，
根据上面结论，可知，
设，
∵，
∴，，
∴，
在中，，即，
解得，
所以的长为；
（2）如图，过点作，取，连接，
∴，
∵四边形是正方形，
∴，
∴，
∴，
在和中，
，
，
∴，
∴线段有最大值时，只需最大即可，
在中，，当三点共线时，，
则的最大值为，
在等腰中，，
∴，
∵，
∴的最大值为，此时，
故答案为：，的最大值为．
【点拨】本题考查了正方形的性质、旋转的性质、三角形全等的判定与性质、勾股定理等知识，较难的是题（2），通过作辅助线，构造全等三角形是解题关键．
试验的种子数
发芽的种子粒数
发芽频率
平行四边形的性质定理3：平行四边形的对角线互相平分．
我们可以用演绎推理证明这个结论
已知：如图，的对角线和相交于点．求证：；．
观察图形，与，与分别属于哪两个三角形？