【赢在高考·黄金8卷】备战2024年高考数学模拟卷（新高考Ⅰ卷专用）黄金卷07及答案

这是一份【赢在高考·黄金8卷】备战2024年高考数学模拟卷（新高考Ⅰ卷专用）黄金卷07及答案，共21页。

黄金卷07
（考试时间：120分钟 试卷满分：150分）
第I卷（选择题）
一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合要求的.
1．已知全集，集合，则（ ）
A．B．C．D．
2．欧拉公式（e为自然对数的底数，为虚数单位）由瑞士数学家Euler（欧拉）首先发现.它将指数函数的定义域扩大到复数，建立了三角函数和指数函数的关系，被称为“数学中的天桥”，则（ ）
A． -1B．1C．-D．
3．若为奇函数，则的值为（ ）
A．-1B．0C．1D．-1或1
4．已知向量满足，且，则在上的投影向量为（ ）
A．B．C．D．
5．已知动点在直线上，过点作圆的一条切线，切点为，则的最小值为（ ）
A．1B．C．D．2
6．“绿水青山，就是金山银山”，随着我国的生态环境越来越好，外出旅游的人越来越多.现有两位游客慕名来江苏旅游，他们分别从“太湖鼋头渚、苏州拙政园、镇江金山寺、常州恐龙园、南京夫子庙、扬州瘦西湖”这6个景点中随机选择1个景点游玩.记事件A为“两位游客中至少有一人选择太湖鼋头渚”，事件B为“两位游客选择的景点不同”，则（ ）
A．B．C．D．
7．玉琮是中国古代玉器中重要的礼器，神人纹玉琮王是新石器时代良渚文化的典型玉器，年出土于浙江省余杭市反山文化遗址.玉琮王通高，孔径、外径.琮体四面各琢刻一完整的兽面神人图像.兽面的两侧各浅浮雕鸟纹.器形呈扁矮的方柱体，内圆外方，上下端为圆面的射，中心有一上下垂直相透的圆孔.试估计该神人纹玉琮王的体积约为（单位：）（ ）
A．B．C．D．
8．如图，已知抛物线（）的焦点为，点（）是抛物线上一点.以为圆心的圆与线段相交于点，与过焦点且垂直于对称轴的直线交于点，，，直线与抛物线的另一交点为，若，则（ ）
A．B．C．D．
二、多项选择题：本题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目的要求，全部选对的得5分，部分选对的得2分，有选错的得0分.
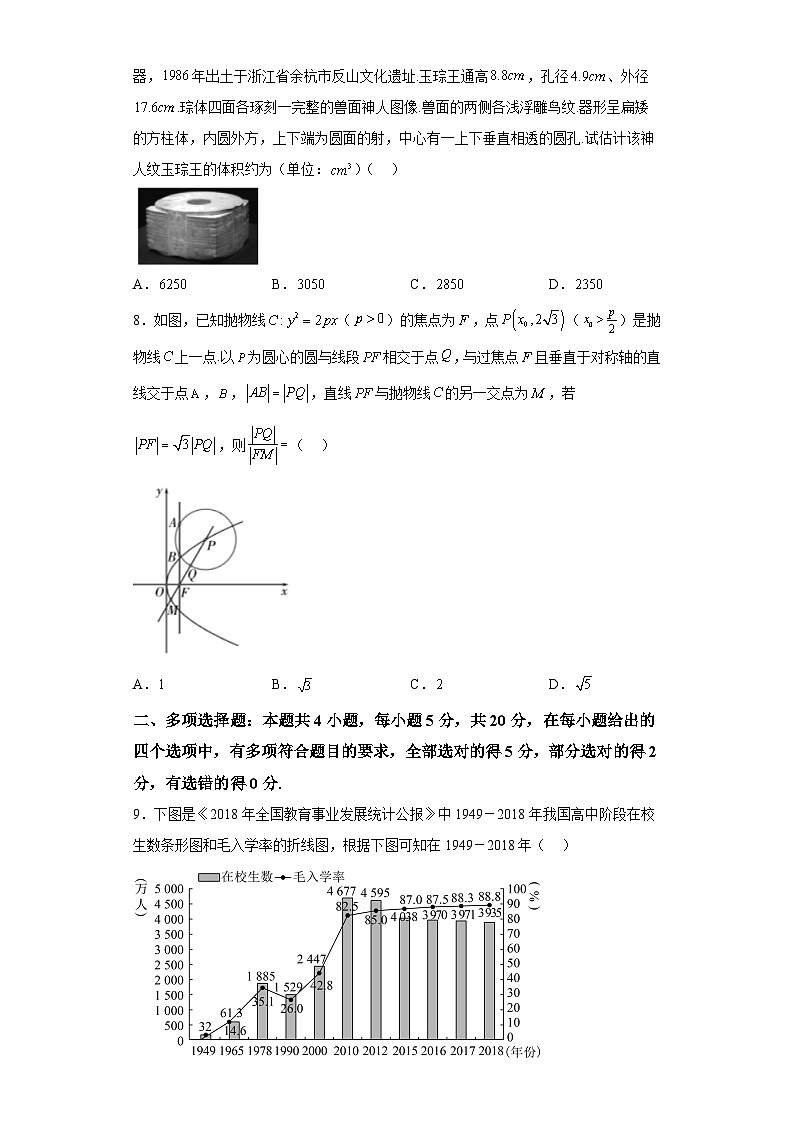
9．下图是《2018年全国教育事业发展统计公报》中1949－2018年我国高中阶段在校生数条形图和毛入学率的折线图，根据下图可知在1949－2018年（ ）
高中阶段在校生数和毛入学率
A．1978年我国高中阶段的在校生数和毛入学率比建国初期大幅度提高
B．从1990年开始，我国高中阶段的在校生数和毛入学率在逐年增高
C．2010年我国高中阶段在校生数和毛入学率均达到了最高峰
D．2018年高中阶段在校生数比2017年下降了约0.91%，而毛入学率提高了0.5个百分点
10．尽管目前人类还无法准确预报地震，但科学家经过研究，已经对地震有所了解，例如，地震时释放的能量E（单位：焦耳）与地震里氏震级M之间的关系为lgE=4.8+1.5M，则下列说法正确的是（ ）
A．地震释放的能量为1015.3焦耳时，地震里氏震级约为七级
B．八级地震释放的能量约为七级地震释放的能量的6.3倍
C．八级地震释放的能量约为六级地震释放的能量的1000倍
D．记地震里氏震级为n（n=1，2，···，9，10），地震释放的能量为an，则数列{an}是等比数列
11．已知双曲线的左、右焦点分别为，，点P在双曲线的右支上，现有四个条件：①；②；③PO平分；④点P关于原点对称的点为Q，且，能使双曲线Ｃ的离心率为的条件组合可以是（ ）
A．①②B．①③C．②③D．②④
12．如图，是底面直径为高为的圆柱的轴截面，四边形绕逆时针旋转到，则（ ）
A．圆柱的侧面积为
B．当时，
C．当时，异面直线与所成的角为
D．面积的最大值为
第II卷（非选择题）
三、填空题：本题共4小题，每小题5分，共20分.
13．编号为1，2，3，4的四位同学，分别就座于编号为1，2，3，4的四个座位上，每位座位恰好坐一位同学，则恰有两位同学编号和座位编号一致的坐法种数为 .
14．已知，则 .
15．已知 a>0，若，且，则a= .
16．已知函数是偶函数，将的图象沿轴向左平移个单位，再将图象上所有点的横坐标伸长到原来的倍（纵坐标不变），所得图象对应的函数为.已知的图象相邻对称中心之间的距离为，则 ，若的图象在其某对称轴处对应的函数值为，则在上的最大值为 .
四、解答题：本题共6小题，共70分，解答应写出必要的文字说明、证明过程及验算步骤.
17．在①；②；③是与的等比中项，三个条件中任选一个，补充在下面问题中，并给出解答.
问题：已知为公差不为零的等差数列，其前项和为为等比数列，其前项和为常数，，
（1）求数列的通项公式；
（2）令其中表示不超过的最大整数，求的值.
注：如果选择多个条件分别解答，按第一个解答计分.
18．如图，平面四边形，点，，均在半径为的圆上，且．
（1）求的长度；
（2）若，求的面积．
19．2021年春晚首次采用“云”传播，“云”互动形式，实现隔空连线心意相通，全球华人心连心“云团圆”，共享新春氛围，“云课堂”亦是一种真正完全突破时空限制的全方位互动性学习模式．某市随机抽取200人对“云课堂”倡议的了解情况进行了问卷调查，记表示了解，表示不了解，统计结果如下表所示：
（表一）
（表二）
（1）请根据所提供的数据，完成上面的列联表（表二），并判断是否有99％的把握认为对“云课堂”倡议的了解情况与性别有关系;
（2）用样本估计总体，将频率视为概率，在男性市民和女性市民中各随机抽取4人，记“4名男性中恰有3人了解云课堂倡议”的概率为，“4名女性中恰有3人了解云课堂倡议”的概率为．试求出与，并比较与的大小．
附：临界值参考表的参考公式
，其中）
20．如图，四棱锥P－ABCD中，PA平面ABCD，AD//BC，∠BAD＝120°，AB＝AD＝2，点M在线段PD上，且DM＝2MP，PB//平面MAC．
(1)求证：平面平面PAD；
(2)若PA＝3，求平面PAB和平面MAC所成锐二面角的余弦值．
21．已知分别是椭圆的左､右焦点， 为椭圆的上顶点，是面积为的直角三角形.
（1）求椭圆的方程；
（2）设圆上任意一点处的切线交椭圆于点，问：是否为定值？若是，求出此定值；若不是，说明理由.
22．已知函数，.
(1)若，讨论的单调性；
(2)若当时，恒成立，求的取值范围.
了解情况
人数
140
60
男
女
合计
80
40
合计
参考答案：
1．A
【解析】先化简集合A，再求得解.
【详解】由题得或，
所以.
故选：A
【点睛】本题主要考查集合的化简和并集运算，意在考查学生对这些知识的理解掌握水平，属于基础题.
2．A
【分析】根据题已知中欧拉公式，直接计算可得答案.
【详解】由题意得：，
故选：A
3．A
【分析】根据奇函数的定义，取特殊情况 ，可以快速求解出的值.
【详解】由题得： ，故.
故选:A.
4．C
【分析】向量在向量上的投影向量的定义计算即可.
【详解】解：因为向量，且，那么，
所以向量在向量上的投影向量为，
故选：C.
5．C
【分析】由题意求出切线长的表达式，结合二次函数的性质即可求解.
【详解】由题可知圆的圆心为，半径为，
设，则，有，
得，
当时，.
故选：C.
6．D
【分析】根据古典概型概率公式求出，然后利用条件概率公式即得.
【详解】由题可得，,
所以.
故选：D.
7．D
【解析】该神人纹玉琮王可看做是一个底面边长为，高为的正四棱柱中挖去一个底面直径为，高为的圆柱，利用圆柱的体积公式计算即可.
【详解】由题可知，该神人纹玉琮王可看做是一个底面边长为，高为的正四棱柱中挖去一个底面直径为，高为的圆柱，此时求得体积记为，
cm3，
记该神人纹玉琮王的实际体积为，
则，
且由题意可知， cm3，
故，
故选：D.
【点睛】本题考查了组合体体积的计算以及柱体体积的计算公式，考查了转化能力，属于中档题.
8．B
【解析】根据抛物线的定义得，直线方程为：，到直线距离为，利用圆的弦，可得，利用，结合抛物线方程，求出和，得到点坐标，联立直线与抛物线方程，求出点坐标，即可求出.
【详解】由题意得，直线方程为：，到直线距离为，
以为圆心的圆与线段相交于点，与过焦点且垂直于对称轴的直线交于点，，，
，
，
，
解得，
，又，故，
抛物线方程为，，，，
直线方程为，
与抛物线方程联立得，
消去整理得，，解得或，
，，
.
故选：B.
【点睛】本题考查了抛物线的方程与定义，考查了直线与圆的位置关系，考查了抛物线与直线的位置关系，考查了转化能力与计算能力，属于中档题.
9．AD
【分析】结合图中的信息对选项逐一分析即可.
【详解】由图可知，1978 年我国高中阶段在校生数和毛入学率比建国初期大幅度提高，选项A 正确；
2012年我国高中阶段在校生数降低，选项 B 错误；
2018年我国高中阶段毛入学率达到了最高峰，选项 C错误；
2018年我国高中阶段在校生数比 2017 年下降了，而毛入学率提高了 ( 个 ) 百分点，选项 D 正确.
故选：AD.
10．ACD
【分析】根据所给公式，结合指对互化原则，逐一分析各个选项，即可得答案.
【详解】对于A：当时，由题意得，
解得，即地震里氏震级约为七级，故A正确；
对于B：八级地震即时，，解得，
所以，
所以八级地震释放的能量约为七级地震释放的能量的倍，故B错误；
对于C：六级地震即时，，解得，
所以，
即八级地震释放的能量约为六级地震释放的能量的1000倍，故C正确；
对于D：由题意得（n=1，2，···，9，10），
所以，所以
所以，即数列{an}是等比数列，故D正确；
故选：ACD
11．AD
【分析】对各个选项进行分析，利用双曲线的定义找到a,c的等量关系，从而确定离心率.
【详解】③PO平分且PO为中线，可得，点P在双曲线的右支上，所以不成立；
若选①②：，，可得，，
所以，即离心率为，成立；
若选②④：，点P关于原点对称的点为Q，且，可得四边形为矩形，即，可得，，
所以，即离心率为，成立；
故选：AD
12．BC
【分析】对于A，由圆柱的侧面积公式可得；
对于B，由线面垂直的判定定理和性质定理可得；
对于C，由题知，为正三角形，根据异面直线所成的角的定义计算得解；
对于D，作，由线面垂直的判定定理和性质定理得.在中，，代三角形面积公式得解.
【详解】对于A，圆柱的侧面积为，A错误；
对于B，因为，所以，又，
所以平面，所以，B正确；
对于C，因为，所以就是异面直线与
所成的角，因为，所以为正三角形，
所以，因为，所以，C正确；
对于D，作，垂足为，连接，所以平面，所以.
在中，，
，所以，D错误.
故选：BC.
13．6
【分析】4人中选2人出来，他们的两编号一致，剩下2人编号不一致，只有一种坐法，由乘法原理可得．
【详解】由题意4人中选2人出来，他们的两编号一致，剩下2人编号不一致，只有一种坐法，方法数为．
故答案为：6.
14．##
【分析】对已知式子利用三角函数恒等变换公式化简变形可得答案.
【详解】由，得
，
，
所以，
所以，
故答案为：
15．2
【分析】依据题给条件列出关于a的方程，解之即可求得a的值.
【详解】因为，
又，展开式通项为，
对应的系数，故得到，解得，
其系数为或.
又a>0，故实数a的值为2.
故答案为：2.
16．
【解析】由题意，根据三角函数图象的对称性求出，根据函数图象的平移变换与拉伸变换，求出的解析式，由已知求出的最小正周期，即可得的值，再结合三角函数的性质，求出，得到的解析式，即可得在上的最大值.
【详解】函数是偶函数，
，，
又，
，
，
将的图象沿轴向左平移个单位，再将图象上所有点的横坐标伸长到原来的倍（纵坐标不变），所得图象对应的函数为，
，
的图象相邻对称中心之间的距离为，
，解得，
的图象在其某对称轴处对应的函数值为，
，
，
当时，，，
故，
在上的最大值为.
故答案为：；.
【点睛】本题考查了三角函数的图象变换以及型函数的性质，考查了转化能力，属于中档题.
17．答案见解析
【分析】若选
（1）先求，可得，进而得，由基本量运算可得；
（2）由，可得解.
若选
（1）先求，可得，进而得，由基本量运算可得；
（2）由，可得解.
若选
（1）先求，可得，进而得，由基本量运算可得；
（2）由，可得解.
【详解】若选：由已知，所以
通项，
故
不妨设的公差为.则
解得所以
由，则，
，
所以.
若选：由已知，，
通项
故.
不妨设的公差为，则，
解得所以.
由，则，
，
所以.
若选：由已知，所以
通项，
故
不妨设的公差为.则，
因为解得所以.
由
则
，
所以.
【点睛】关键点点睛：本题解题的关键一是利用基本量运算求解通项公式，二是根据判断的值.
18．（1）5（2）
【解析】（1）先求出的外接圆半径为，再利用正弦定理求出得解；（2）设，为锐角，则，先求出，再利用余弦定理求出
，即得的面积．
【详解】（1）由题意可知，的外接圆半径为，
由正弦定理，解得；
（2）在中，设，为锐角，则，
因为，
所以，
所以，
因为，
即，
所以，
则，
所以，
【点睛】本题主要考查正弦余弦定理解三角形，考查三角形面积的计算，意在考查学生对这些知识的理解掌握水平.
19．（1）表格见解析，有；（2），，.
【分析】（1）依据题中数据直接填写，然后根据公式计算即可.
（2）先计算男性了解“云课堂”倡议的概率，女性了解“云课堂”倡议的概率，然后可得，进行比较即可.
【详解】（1）
．
对照临界值表知，有99％的把握认为对“云课堂”倡议了解情况与性别有关系．
（2）用样本估计总体，将频率视为概率，根据列联表得出，
男性了解“云课堂”倡议的概率为，
女性了解“云课堂”倡议的概率为：，
故，，
显然．
20．(1)证明见解析；
(2)．
【分析】(1)连接BD交AC于点E，连接ME，由所给条件推理出CA⊥AD，进而得CA⊥平面PAD，证得结论．
(2)首先以A为原点，射线AC，AD，AP分别为x，y，z轴非负半轴建立空间直角坐标系，再利用向量法求解二面角即可．
【详解】(1) 连接BD交AC于点E，连接ME，如图所示：
∵PB//平面MAC，PB平面PBD，平面PBD平面MAC=ME，
∴PB//ME，，则BC=1，而AB=2，，
，
∴AC2+BC2=4=AB2，∠ACB=90º，∠CAD=90º，即CA⊥AD，
又PA⊥平面ABCD，CA平面ABCD，∴PA⊥CA，又PAAD=A，∴CA⊥平面PAD，而CA平面MAC，∴平面MAC⊥平面PAD．
(2)如图所示：
以A为原点，射线AC，AD，AP分别为x，y，z轴非负半轴建立空间直角坐标系，
则，
∴，
设平面PAB和平面MAC的一个法向量分别为，
平面PAB和平面MAC所成锐二面角为，
∴，，
∴.
【点睛】(1)证面面垂直，关键是在其中一个平面内找到一条直线，证它垂直于另一个平面；
(2)几何体中，有共点的三线两两垂直，涉及求距离、求角的问题，建立空间直角坐标系，转化为用空间向量求解.
21．（1）；（2）是定值，定值为.
【分析】（1）由题意可得，再由即可求解.
（2）当切线的斜率不存在时，其方程为，求出，当切线的斜率存在时，设方程为，利用点到直线的距离公式可得，再将直线与椭圆联立，利用韦达定理可得，再由即可求解.
【详解】解：（1）由为直角三角形，故，
又，
可得
解得
所以，
所以椭圆的方程为；
（2）当切线的斜率不存在时，其方程为
将代入，得，不妨设，，又
所以
同理当时，也有.
当切线的斜率存在时，设方程为，
因为与圆相切，
所以
即，
将代入，
得，
所以
又
，
又
，
将代入上式，得，
综上，.
【点睛】关键点点睛：本题考查了直线与椭圆的位置关系，解题的关键是根据直线与椭圆相切可得，再求证，考查了运算求解能力、分析能力以及分类讨论的思想.
22．(1)函数的单调递增区间为，无递减区间
(2)
【分析】（1）求出函数的定义域，利用函数的单调性与导数的关系可得出函数的增区间和减区间；
（2）设，可知对任意的恒成立，对实数的取值进行分类讨论，利用导数分析函数在上的单调性，验证对任意的能否恒成立，综合可得出实数的取值范围.
【详解】（1）解：的定义域为，当时，，
，
设，则，
令，解得，
当时，，单调递减，
当，，单调递增.
所以，，则对任意的恒成立，
所以，函数的单调递增区间为，无递减区间.
（2）解：当时，恒成立等价于在上恒成立，
设，
则，
设，
则图象为开口向上，对称轴为的抛物线的一部分，
当时，，在单调递增，且，
所以，，即，则函数在上单调递增，
又因为，所以在恒成立，满足题意；
当时，，，
所以方程有两相异实根，设为、，且，则，
当时，，，在上单调递减，
又因为，故当时，，
所以，在上不恒成立，不满足题意.
综上，的取值范围为.
【点睛】关键点点睛：本题考查利用函数不等式恒成立求参数的取值范围，注意到，由此将问题转化为考查函数在上的单调性来处理，只需对实数的取值进行分类讨论，结合单调性来求解.
男
女
合计
80
60
140
20
40
60
合计
100
100
200