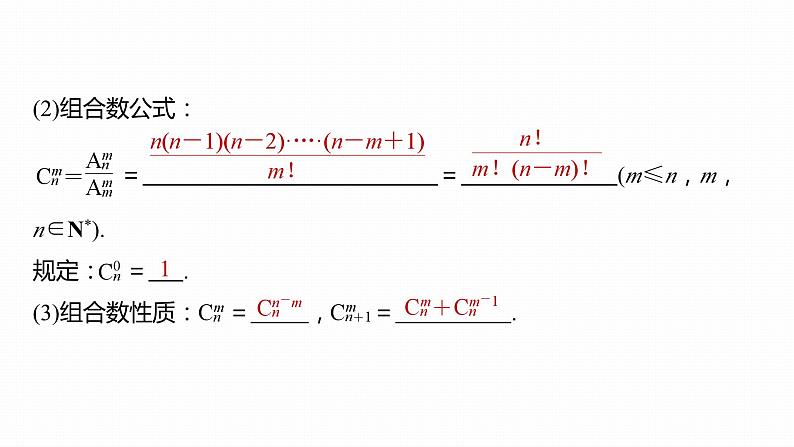
高考数学考前回顾复习《概率与统计》课件

这是一份高考数学考前回顾复习《概率与统计》课件，共56页。PPT课件主要包含了必考知识，常用结论，经典重温，n－1，PA＋PB，PAPB，aEX＋b，a2DX，p1－p，np1－p等内容，欢迎下载使用。
1.排列数、组合数公式，组合数的性质(1)排列数公式： ＝n(n－1)(n－2)·…·(n－m＋1)＝ (m≤n，m，n∈N*).规定：0！＝ .
(2)组合数公式： ＝ ＝ (m≤n，m，n∈N*).规定： ＝ .(3)组合数性质： ＝ ， ＝ .
2.二项式定理及二项展开式的通项公式二项式定理：(a＋b)n＝ .二项展开式的通项：Tk＋1＝ (k＝0,1，…，n).
(3)最值：n为偶数时，中间一项的二项式系数最大且二项式系数为 ；n为奇数时，中间两项的二项式系数最大.
4.随机事件之间的关系(1)必然事件Ω，P(Ω)＝1；不可能事件∅，P(∅)＝0.(2)包含关系：A⊆B，“如果事件A发生则事件B一定发生”称事件B包含事件A.(3)事件的和(并)：A＋B或A∪B，“事件A与事件B至少有一个发生”叫做事件A与事件B的和(并)事件.(4)事件的积(交)：AB或A∩B，“事件A与事件B同时发生”叫做事件A与事件B的积(交)事件.
5.概率的计算公式(1)古典概型的概率计算公式P(A)＝ .(2)若A，B互斥，则P(A＋B)＝ .(3)P(A)＝1－ .(4)若A，B相互独立，则P(AB)＝ .(5)如果在一次试验中A发生的概率是p(00，i＝1,2，…，n，则对任意的事件B⊆Ω，P(B)>0，有
6.离散型随机变量的均值和方差(1)公式：E(X)＝ ＝D(X)＝ ＝
x1p1＋x2p2＋…＋xnpn
(x1－E(X))2p1＋(x2－E(X))2p2＋…＋(xn－E(X))2pn
(2)均值、方差的性质：①E(k)＝k(k为常数)，D(k)＝0(k为常数).②E(aX＋b)＝ ，D(aX＋b)＝ .
(3)两点分布与二项分布的均值与方差①若随机变量X服从两点分布，则E(X)＝ ，D(X)＝ .②若随机变量X服从二项分布，即X～B(n，p)，则E(X)＝ ，D(X)＝ .
7.常用的抽样方法简单随机抽样、分层随机抽样.8.统计中的四个数据(1)众数：在样本数据中，出现次数最多的那个数据.(2)中位数：在样本数据中，将数据按大小依次排列，位于最中间的数据.如果数据的个数为偶数，就取中间两个数据的平均数作为中位数.
(4)方差与标准差方差：s2＝ .标准差：s＝ .
11.正态分布如果随机变量X服从正态分布，则记为X～N(μ，σ2).X落在三个特殊区间的概率为(1)P(μ－σ≤X≤μ＋σ)≈0.682 7；(2)P(μ－2σ≤X≤μ＋2σ)≈0.954 5；(3)P(μ－3σ≤X≤μ＋3σ)≈0.997 3.
1.求解排列问题常用的方法
2.古典概型中样本点个数的确定方法
3.频率分布直方图中的众数、中位数、平均数(1)最高的小长方形底边中点的横坐标为众数；(2)中位数左边和右边的小长方形的面积和是相等的；(3)平均数是频率分布直方图的“重心”，其估计值等于频率分布直方图中每个小长方形的面积乘以小长方形底边中点的横坐标之和.
4.样本相关系数r可以表示两个变量间的相关性当r>0时，表明两个变量正相关；当r