高考数学考前回顾复习《数　列》课件

这是一份高考数学考前回顾复习《数　列》课件，共32页。PPT课件主要包含了必考知识，常用结论，经典重温，a1＋n－1d，a1qn－1，na1，am＋an＝，ap＋aq，n－m，qn－m等内容，欢迎下载使用。
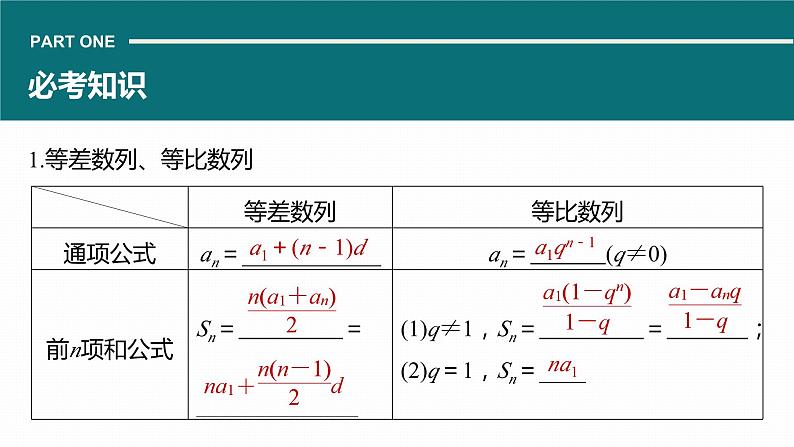
1.等差数列、等比数列
2.判断或证明一个数列是等差(等比)数列的方法判断一个数列为等差(等比)数列的方法有：定义法、中项公式法、通项公式法、前n项和公式法；证明一个数列为等差(等比)数列的方法只有定义法、中项公式法.
3.等差数列、等比数列{an}的常用性质
am·an＝as·at
4.数列求和的方法(1)公式法：等差数列或等比数列的求和，直接利用公式求和.(2)错位相减法：形如{an·bn}(其中{an}为等差数列，{bn}为等比数列)的数列，利用错位相减法求和.
(4)并项求和法：先将某些项放在一起求和，然后再求Sn.通项公式形如an＝(－1)n·n或an＝a·(－1)n(其中a为常数，n∈N*)等正负项交叉的数列求和一般用并项法.并项时应注意分n为奇数、偶数两种情况讨论.(5)分组求和法：分组求和法是解决通项公式可以写成cn＝an±bn形式的数列求和问题的方法，其中{an}与{bn}是等差(等比)数列或一些可以直接求和的数列.
1.等差数列的重要结论设Sn为等差数列{an}的前n项和，则(1)an能写成an＝dn＋a的形式，Sn能写成Sn＝An2＋Bn的形式，其中a≠0.
2.等比数列的重要结论(1)an＝kqn－1为指数型函数，Sn＝A·qn－A.(2){an}，{bn}成等比数列⇒{anbn}成等比数列.(3)连续m项的和(如Sm，S2m－Sm，S3m－S2m，…)仍然成等比数列(注意：这连续m项的和必须非零才能成立).(4)若等比数列有2n项，公比为q，奇数项之和为S奇，偶数项之和为S偶，则 ＝q.(5)等比数列前n项和有：①Sm＋n＝Sm＋qmSn；
由题意可知，若数列{an}为“梦想数列”，
即正项数列{bn}是公比为2的等比数列，因为b1＋b2＋b3＝1，所以b6＋b7＋b8＝25(b1＋b2＋b3)＝32.
2.在等差数列{an}中，a2＝4，且a1，a3，a9构成等比数列，则公差d等于A.0或2 B.2C.0 D.0或－2
因为在等差数列{an}中，a2＝4，且a1，a3，a9构成等比数列，
即(a2＋d)2＝(a2－d)(a2＋7d)，所以(4＋d)2＝(4－d)(4＋7d)，解得d＝0或d＝2.
3.如图是瑞典数学家科赫在1904年构造的能够描述雪花形状的图案.图形的作法是：从一个正三角形开始，把每条边分成三等份，然后以各边的中间一段为底边分别向外作正三角形，再去掉底边.反复进行这一过程，就得到一条“雪花”状的曲线.设原正三角形(图①)的边长为1，把图①，图②，图③，图④中图形的周长依次记为C1，C2，C3，C4，则C4等于
5.(多选)(2023·鞍山模拟)下列命题正确的有A.若等差数列{an}的前n项和为Sn，则S3，S6，S9成等差数列B.若{an}为等比数列，且a2a7＋a3a6＝6，则a1a2a3·…·a8＝81C.若等差数列{an}的前n项和为Sn，且S14>0，S15a2>…>a7>0>a8>a9>…，所以数列的前7项和最大，故C正确；对于D，因为bn＝(－1)n(4n－1)，所以数列{bn}的前2 024项和S2 024＝(－3＋7)＋(－11＋15)＋…＋[－(4×2 023－1)＋(4×2 024－1)]＝1 012×4＝4 048，故D正确.
6.已知数列{an}，{bn}都是等差数列，且a1＝5，b1＝15，a100＋b100＝100，则数列{an＋bn}的前100项和为________.
因为数列{an}，{bn}都是等差数列，所以{an＋bn}也是等差数列，又a1＝5，b1＝15，a100＋b100＝100，
7.(2023·广州模拟)若数列{an}对任意正整数n，有an＋m＝anq(其中m∈N*，q为常数，q≠0，q≠1)，则称数列{an}是以m为周期，q为周期公比的“类周期性等比数列”.若“类周期性等比数列”的前4项为1,1,2,3，周期为4，周期公比为3，则数列{an}的前21项和为_________.
由题意可知m＝4，q＝3，且an＋4＝3an，故S21＝(a1＋a5＋a9＋a13＋a17＋a21)＋(a2＋a6＋a10＋a14＋a18)＋(a3＋a7＋a11＋a15＋a19)＋(a4＋a8＋a12＋a16＋a20)
＝364＋121＋242＋363＝1 090.
因为Sn为数列{an}的前n项和，
所以当n＝1时，a1＝S1＝1，
因为当n＝1时也满足an＝n，所以an＝n，
9.已知等差数列{an}的前n项和为Sn，且S4＝4S2，a2n＝2an＋1(n∈N*).(1)求数列{an}的通项公式；
所以数列{an}的通项公式an＝1＋(n－1)×2＝2n－1.
(2)若bn＝3n－1，令cn＝anbn，求数列{cn}的前n项和Tn.
因为cn＝anbn＝(2n－1)3n－1，所以Tn＝1×30＋3×31＋5×32＋…＋(2n－1)×3n－1，①①×3得3Tn＝1×31＋3×32＋5×33＋…＋(2n－1)×3n，②①－②得－2Tn＝1×30＋2×31＋2×32＋…＋2×3n－1－(2n－1)×3n＝1＋2(31＋32＋…＋3n－1)－(2n－1)×3n
化简得Tn＝(n－1)3n＋1.
10.(2023·乌鲁木齐模拟)设数列{an}满足a1＝－3，an＋1＝2an＋3n－1，{an}的前n项和为Sn.(1)证明：{an＋3n＋2}为等比数列；
因为an＋1＝2an＋3n－1，所以an＋1＋3(n＋1)＋2＝2an＋3n－1＋3(n＋1)＋2＝2(an＋3n＋2).因为a1＝－3，所以{an＋3n＋2}是首项为2，公比为2的等比数列.
(2)求数列{Sn}中的最小项.