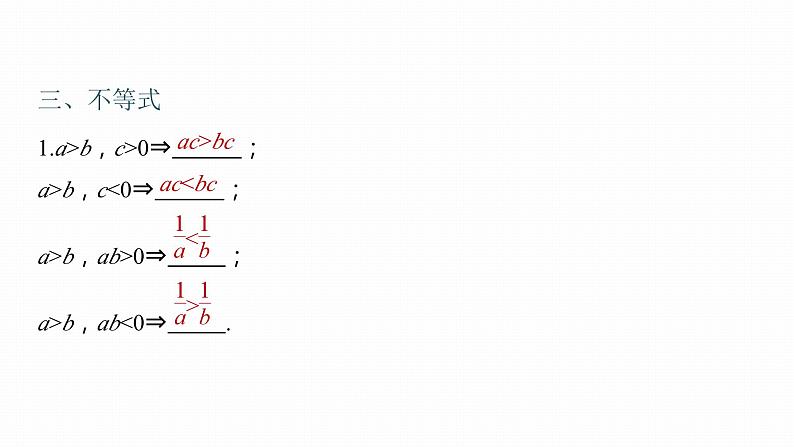
高考数学考前回顾复习《非主干内容》课件

这是一份高考数学考前回顾复习《非主干内容》课件，共33页。PPT课件主要包含了确定性，互异性，无序性，AB，BA，A＝B，平面向量，三个公式，不等式，acbc等内容，欢迎下载使用。

1.集合元素的特征： 、 、 .2.集合的运算性质(1)若A⊆B，则A∩B＝ ，A∪B＝ .(2)A∩∅＝ ，A∪∅＝ .(3)∁U(∁UA)＝ .
一、集合与常用逻辑用语
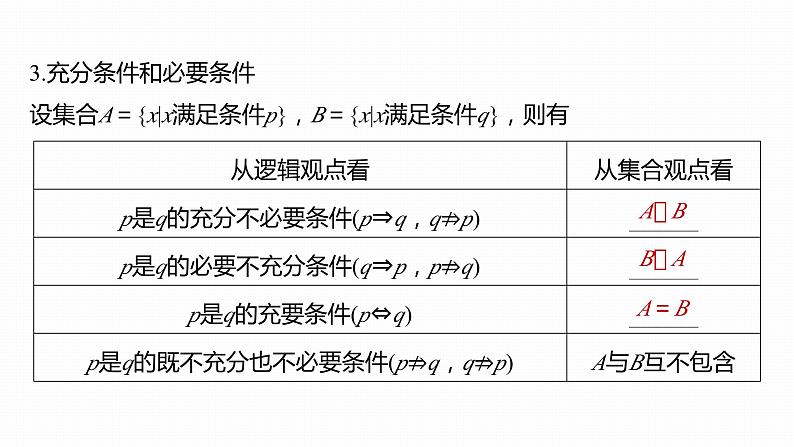
3.充分条件和必要条件设集合A＝{x|x满足条件p}，B＝{x|x满足条件q}，则有
1.两个向量两个非零向量平行、垂直的充要条件：若a＝(x1，y1)，b＝(x2，y2)，则(1)a∥b⇔a＝λb(b≠0)⇔x1y2－x2y1＝0.(2)a⊥b⇔a·b＝0⇔x1x2＋y1y2＝0.
1.a>b，c>0⇒ ；a>b，c<0⇒ ；a>b，ab>0⇒ ；a>b，ab<0⇒ .
1.两个复数相等a＋bi＝c＋di⇔ (a，b，c，d∈R).2.复数的运算法则(a＋bi)±(c＋di)＝ ；(a＋bi)(c＋di)＝ ；(a＋bi)÷(c＋di)＝ (c＋di≠0)(其中a，b，c，d∈R).
(a±c)＋(b±d)i
(ac－bd)＋(ad＋bc)i
3.复数的几何意义(1)复数z＝a＋bi(a，b∈R)的模|z|＝ .(2)若复数z满足|z－(1＋i)|＝1，则复数z在复平面上对应点的轨迹是 .
以点(1,1)为圆心，以1为半径的圆
1.若集合A有n个元素，则其子集个数为2n，真子集个数为2n－1，非空真子集个数为2n－2.
3.若a与b不共线，且λa＋μb＝0，则λ＝μ＝0.
5.三角形“四心”向量形式的充要条件设O为△ABC所在平面内一点，内角A，B，C所对的边分别为a，b，c，则
1.设全集U＝R，集合A＝{x||x－2|≤1}，B＝{x|2x－4≥0}，则集合A∩(∁UB)等于A.(1,2) B.(1,2]C.[1,2) D.[1,2]
解不等式|x－2|≤1得1≤x≤3，则A＝[1,3]，解不等式2x－4≥0，得x≥2，则B＝[2，＋∞)，∁UB＝(－∞，2)，所以A∩(∁UB)＝[1,2).
2.已知(1＋i)z＝2i，则复数z的共轭复数是A.1＋i B.－1＋iC.1－i D.－1－i
所以复数z的共轭复数是1－i.
3.若不等式|x－1|0 B.a≥0C.a>1 D.a≥1
由不等式|x－1|4.若命题“∃a∈[－1,3]，ax2－(2a－1)x＋3－a<0”为假命题，则实数x的取值范围为
若命题“∃a∈[－1,3]，ax2－(2a－1)x＋3－a<0”为假命题，则其否定为真命题，即“∀a∈[－1,3]，ax2－(2a－1)x＋3－a≥0”为真命题.令g(a)＝ax2－2ax＋x＋3－a＝(x2－2x－1)a＋x＋3≥0，
设等腰△ABC中，AB＝AC＝1，则由余弦定理可知BC2＝AB2＋AC2－2AB·AC·cs 120°＝1＋1＋1＝3，
∵ AD平分∠BAC且与BC相交于点D，△ABC是等腰三角形，
作DE垂直于AB交AB于点E，
6.(多选)已知复数z1＝－2＋i(i为虚数单位)在复平面内的对应的点为A，复数z2满足|z2－1＋i|＝2，z2在复平面内对应的点B的坐标为(x，y)，则下列结论正确的有A.复数z1的虚部为iB.(x－1)2＋(y＋1)2＝4
由z1＝－2＋i，得复数z1虚部为1，故A错误；因为|z2－1＋i|＝2，z2在复平面内对应的点B的坐标为(x，y)，则|(x－1)＋(y＋1)i|＝2，点B在以(1，－1)为圆心，2为半径的圆周上，所以(x－1)2＋(y＋1)2＝4，故B正确；根据复数的几何意义，知|AB|＝|z1－z2|，
∵m>0，n>0，m＋n＝2，
∴mn≤1，当且仅当m＝n＝1时，等号成立，故B正确；
当且仅当m＝n＝1时，等号成立，故C错误；m2＋n2＝(m＋n)2－2mn＝4－2mn≥2，当且仅当m＝n＝1时，等号成立，故D错误.
8.已知命题p：∀x∈(0，＋∞)，ex>x＋1，则p的否定为_________________________.
由全称量词命题的否定是存在量词命题知p的否定：∃x∈(0，＋∞)，ex≤x＋1.
9.(2023·重庆模拟)已知正实数x，y满足4x2－9xy＋2y2＝－4，且 因为4x2－9xy＋2y2＝(4x－y)(x－2y)＝－4，所以(4x－y)(2y－x)＝4，
所以3x＋y的最小值为4.