









高中数学人教B版 (2019)必修 第一册3.1.3 函数的奇偶性精品课件ppt
展开(1)本节将要研究哪类问题?
(2)本节研究的起点是什么?目标是什么?
问题1 阅读课本第107~109,回答下列问题:
问题2 上节课我们学习了哪些知识?
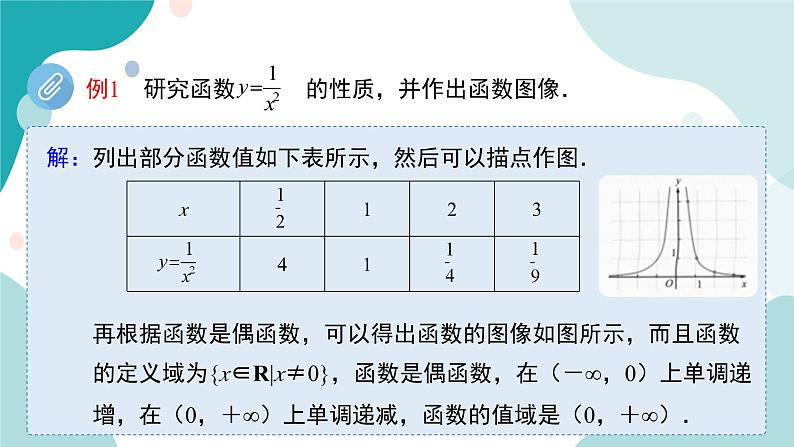
例1 研究函数 的性质,并作出函数图像.
要使函数表达式意义,需有x≠0,因此函数的定义域为
D={x∈R|x≠0},
从而可知函数的图像有左右两部分.
下面研究函数在区间(0,+∞)上的性质及图像.
因为x1,x2∈(0,+∞)时,有
又因为x∈(0,+∞)时,
所以函数图像在右边的部分一定在第一象限.
列出部分函数值如下表所示,然后可以描点作图.
再根据函数是偶函数,可以得出函数的图像如图所示,而且函数的定义域为{x∈R|x≠0},函数是偶函数,在(-∞,0)上单调递增,在(0,+∞)上单调递减,函数的值域是(0,+∞).
拓展:对于该函数,当且无限增大时,且无限接近于0;当且无限接近于0时,且无限增大.利用研究奇偶函数的类似方法还可以研究更一般的函数图像的性质.
例2 研究函数 的性质,并作出函数图像.
所以函数f(x)是一个奇函数.
因此,f(x)的定义域为D={x∈R|x≠0},值域 为(-∞,-2]∪[2,+∞),而且f(x)在 (0,1 ]和[-1,0)上递减,在(-∞,-1]和[1,+∞)上递增,函数在定义域内没有最值.
描点作图,可画出x>0时f(x)的大致图像.再根据f(x)是一个奇函数,可知其图像如图所示.
例3 求证:二次函数f(x)=x2+4x+6的图像关于x=-2对称.
f(-2+h)=(-2+h)2+4(-2+h)+6=h2+2,
f(-2-h)=(-2-h)2+4(-2-h)+6=h2+2,
所以f(-2+h)=f(-2-h),这就说明函数的图像关于x=-2对称.
1.注意到f(x)=x2+4x+6=(x+2)2+2,由此就容易得到f(-2+h)=f(-2-h),从而可知f(x)图像的对称轴为x=-2.
2.二次函数对称轴的寻找,除了使用配方法来理解之外,也可以使用函数变换的思想来理解.
3.一般地,通过函数变换可得到如下结论:
这就是说,所有图像关于直线x=a(a≠0)对称的函数,都可以由偶函数经过平移得到;所有图像关于某一个点(不是原点)对称的函数,都可以由奇函数经过平移得到.
(1)函数f(x)的图像关于x=a对称,当且仅当f(x+a)为偶函数;
(2)函数f(x)的图像关于(a,b)对称,当且仅当f(x+a)-b 为奇函数.
【探索与研究】(1)如果一个函数是奇函数,那么其值域具有什么特点?
(2)怎样才能证明函教的图像关于点(3,0)对称?一般地,怎样证明函数的图像关于点(a,b)对称?
(1)如果一个函数是奇函数,那么其值域一定关于原点对称.更进一步,此时如果函数在x0处取得最大值M,那么该函数在-x0处取得最小值-M.
(2)设函数f(x)的定义域为D; 如果对于任意的3-x∈D,都有3+ x∈D,且f(3-x)=- f(3+x),那么函数f(x)的图像关于点(3,0)对称;如果对于任意的a-x∈D,都有a+x∈D. 且f(a-x)+ f(a+x)=2b,那么函数f(x)的图像关于点(a,b)对称.
设f(x)是R上的偶函数,且在[0,+∞)上单调递增,则f(-2),f(-π),f(3)的大小顺序是( )
∴f(-2)=f(2),f(-π)=f(π),
∴f(π)>f(3)>f(2),即f(-π)>f(3)>f(-2).故选A.
A.f(-π)>f(3)>f(-2) B.f(-π)>f(-2)>f(3)C.f(3)>f(-2)>f(-π) D.f(3)>f(-π)>f(-2)
又f(x)在[0,+∞)上单调递增,且2<3<π,
∵f(x)是R上的偶函数,
函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( )
A.[-2,2] B.[-1,1] C.[0,4] D.[1,3]
故由-1≤f(x-2)≤1,
∴1≤x≤3. 故选D.
又f(x)在(-∞,+∞)单调递减,∴-1≤x-2≤1,
∵f(x)为奇函数,∴f(-x)=-f(x).
∵f(1)=-1,∴f(-1)=-f(1)=1.
得f(1)≤f(x-2)≤f(-1).
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有 <0.则( )
A.f(3)<f(-2)<f(1) B.f(1)<f(-2)<f(3)C.f(-2)<f(1)<f(3) D.f(3)<f(1)<f(-2)
已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,那么,不等式f(x+2)<5的解集是__________.
∴|x+2|<5,解得:-7<x<3,
所以解集为(-7,3).
由当x≥0时,f(x)=x2-4x,知:
f(x+2)<5=f(5),
又f(x)是定义域为R的偶函数,
问题3 回顾本节课,你有什么收获?
(1)函数的奇偶性与单调性之间有什么样的关系?
(2)你知道函数f(x)=x+ 的图像和性质吗?
(3)如何说明函数的图像关于点或垂直于x轴的直线对称?
作业:教科书P110练习B 5、7
高中数学人教B版 (2019)必修 第一册3.1.3 函数的奇偶性完美版ppt课件: 这是一份高中数学人教B版 (2019)必修 第一册<a href="/sx/tb_c4000124_t3/?tag_id=26" target="_blank">3.1.3 函数的奇偶性完美版ppt课件</a>,文件包含313《函数的奇偶性》第2课时课件pptx、313《函数的奇偶性》第2课时教案docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
人教B版 (2019)必修 第一册3.1.3 函数的奇偶性精品课件ppt: 这是一份人教B版 (2019)必修 第一册<a href="/sx/tb_c4000124_t3/?tag_id=26" target="_blank">3.1.3 函数的奇偶性精品课件ppt</a>,文件包含313《函数的奇偶性》第1课时课件pptx、313《函数的奇偶性》第1课时教案docx等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
高中人教B版 (2019)3.1.3 函数的奇偶性课文配套ppt课件: 这是一份高中人教B版 (2019)3.1.3 函数的奇偶性课文配套ppt课件













