黑龙江省哈尔滨市第六十九中学2023-2024学年八年级下学期月考数学试题(含答案)

这是一份黑龙江省哈尔滨市第六十九中学2023-2024学年八年级下学期月考数学试题(含答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（每小题3分，共计30分）
1．【教材P14－1】以下列各组线段为边，不能构成直角三角形的是（ ）
A．7cm，24cm，25cmB．，4cm，5cm
C．，1cm，D．40cm，50cm，60cm
2．【教材P6－2】在平面直角坐标系中，点P（－4，3）到原点的距离是（ ）
A．3B．4C．5D．7
3．【教材P8－2】如图，一木杆在离地面3m处折断，木杆顶端落在距离木杆底端4m处，木杆在折断之前的高度为（ ）
A．5米B．7米C．8米D．12米
4．【概念定理】如图，在Rt△ABC中，∠B=90°，BC=12，AB=5，则斜边上的中线BO长是（ ）
A．2.5B．4C．6D．6.5
5．【概念定理】在四边形ABCD中，O是对角线交点，下列条件中，不能判定四边形ABCD是平行四边形的是（ ）
A．，AD=BCB．AB=DC，AD=BC
C．OA=OC，OD=OBD．，AD=BC
6．【教材P7－例】已知线段AB，按如下步骤作图：①作射线AC，使AC⊥AB；②作∠BAC的平分线AD；③以点A为圆心，AB长为半径作弧，交AD于点E；④过点E作EP⊥AB于点P，则AP：AB=（ ）．
A．B．1：2C．D．
7．【教材P5－例2】如图，一架2.5米长的梯子AB斜立在一竖直的墙上，这时梯足B与墙底端O距离0.7米．如果梯子的顶端A沿墙下滑0.4米至点C处，那么梯足B将向外滑动（ ）至点D处．
A．0.9米B．1.5米C．0.5米D．0.8米
8．【教材P14－2】下列命题中，其逆命题成立的有（ ）个．
①同旁内角互补，两直线平行； ②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等； ④矩形的对角线互相平分且相等．
A．1B．2C．3D．42
9．【资P4－24】如图，矩形纸片ABCD中，已知BC=8，折叠纸片使点B与对角线AC上的点F重合，折痕为AE，若EF=3，则AB的长等于（ ）．
A．4B．5C．6D．
10．【教材P19－13】有一个长方体的铁盒，长、宽、高分别是5cm，4cm，3cm，则这个铁盒中能放入的木棒最长为（ ）cm．（铁盒的厚度忽略不计）
A．7B．8C．D．
二、填空题（每小题3分，共计30分）
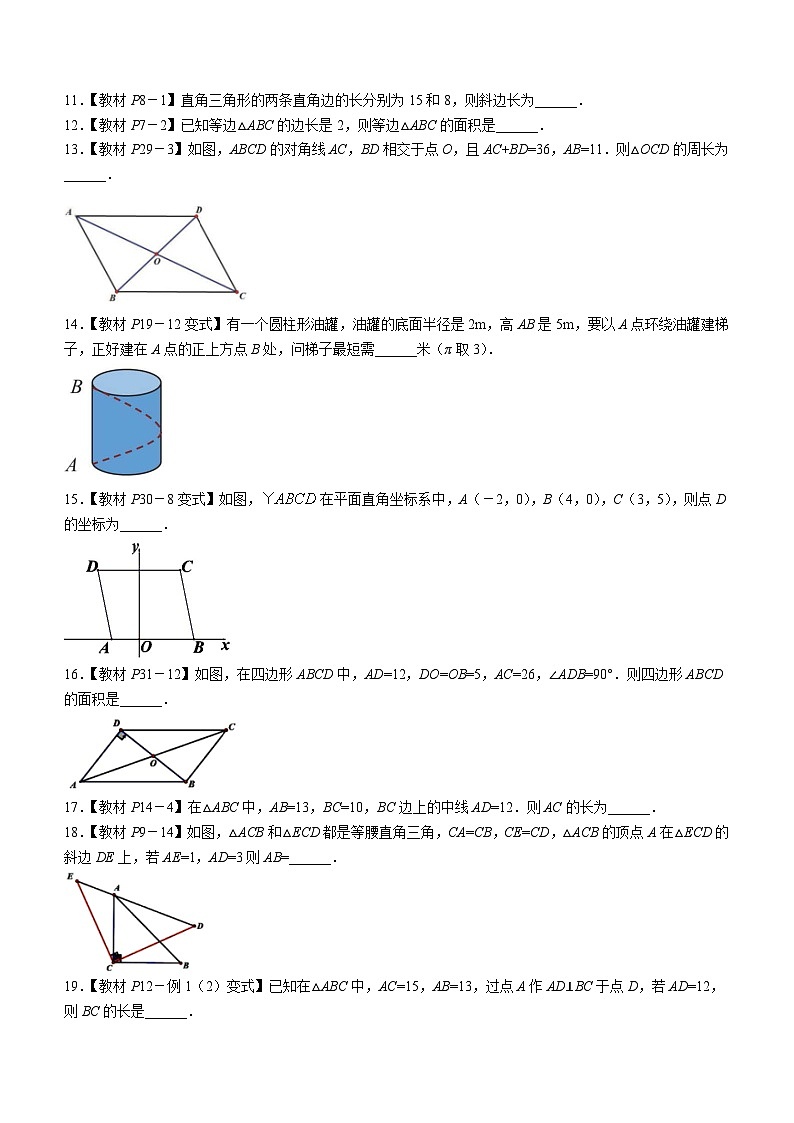
11．【教材P8－1】直角三角形的两条直角边的长分别为15和8，则斜边长为______．
12．【教材P7－2】已知等边△ABC的边长是2，则等边△ABC的面积是______．
13．【教材P29－3】如图，ABCD的对角线AC，BD相交于点O，且AC+BD=36，AB=11．则△OCD的周长为______．
14．【教材P19－12变式】有一个圆柱形油罐，油罐的底面半径是2m，高AB是5m，要以A点环绕油罐建梯子，正好建在A点的正上方点B处，问梯子最短需______米（π取3）．
15．【教材P30－8变式】如图，在平面直角坐标系中，A（－2，0），B（4，0），C（3，5），则点D的坐标为______．
16．【教材P31－12】如图，在四边形ABCD中，AD=12，DO=OB=5，AC=26，∠ADB=90°．则四边形ABCD的面积是______．
17．【教材P14－4】在△ABC中，AB=13，BC=10，BC边上的中线AD=12．则AC的长为______．
18．【教材P9－14】如图，△ACB和△ECD都是等腰直角三角，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边DE上，若AE=1，AD=3则AB=______．
19．【教材P12－例1（2）变式】已知在△ABC中，AC=15，AB=13，过点A作AD⊥BC于点D，若AD=12，则BC的长是______．
20．如图，在四边形ABCD中，∠ABC=45°，对角线AC与BD互相垂直，∠CAD=2∠ABD．过点A作AE⊥BC于E，AE交BD于点F，若F为DB的中点，，则BC=______．
三、解答题（21、22题7分，23、24题8分，25、26、27题10分，共计30分）
21．图（1）、图（2）是两张形状，大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，请在图（1）、图（2）网格中分别画出符合要求的图形．（所画图形各顶点必须与方格纸中的小正方形顶点重合，并且用格尺规范作图）．
（1）在图（1）中画出一个，使其周长为；
直接写出图（1）中你所画出的的面积为______．
（2）在图（2）画出一个周长为20，面积为24的矩形EFMN．
22．【教材P26－例3】如图，的对角线AC，BD相交于点O，E、F是AC上的两点，并且AE=CF．求证：四边形BFDE是平行四边形．
23．【教材P14－5】如图，在四边形ABCD中，AB=3，BC=4，CD=12，AD=13，∠B=90°，求四边形ABCD的面积．
24．【教材P13－例2变式】如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进20海里到达B点，此时，测得海岛C位于北偏东30°的方向，求海岛C到航线AB的距离CD．
25．如图，在△ABC中，∠BAC=90°，AB=AC=5，点D在AC上，点E在AB上，连接DE，点F，G分别是BC和DE的中点，连接AG，FG，且AG=FG，连接DF，EF．
（1）求证：∠DFE=90°
（2）若AD=m，则用含m的式子表示线段BE的长；
（3）在（2）问的条件下，当m=2时，求线段DE长．
26．【数资P40－23】如图所示，四边形ABCD为平行四边形，点P是CD边上一点，连接AP、BP，且AP和BP分别平分∠DAB和∠CBA．
（1）如图1，求∠APB的度数；
（2）如图2，如果AD=5，AP=8，求△APB的周长．
（3）如图2，点E、F在线段AB上，连接PE、PF，若∠EPF=60°，AE=BF，PE=20，PF=12，求DC的长度．
69中八年级3月月考26题（24年）
26．【数资P40－23】如图所示，四边形ABCD为平行四边形，点P是CD边上一点，连接AP、BP，且AP和BP分别平分∠DAB和∠CBA．
（1）如图1，求∠APB的度数；
（2）如图2，如果AD=5，AP=8，求△APB的周长．
（3）如图2，点E、F在线段AB上，连接PE、PF，若∠EPF=60°，AE=BE，PE=20，PF=12，求DC的长度．
69中八年级3月月考27题（24年）
27．如图，在平面直角坐标系中，点A、点B分别在x轴和y轴的正半轴上，点C在第一象限内，AC⊥x轴于点A，AC=BO，BC=2．
（1）求点A的坐标．
（2）D为OB的中点，P是BC边上一点，连接AP，AD，∠APC=2∠OAD，设P的横坐标为t，AP的长度为d，求d关于t的关系式．
（3）在（2）的条件下，过点B作BE⊥AP交AP的延长线于E，交AC的延长线于F，G是线段AC上的点，连接OG交AD于点Q，交AE于点H，连接OE、CE，若OE=2EC，OG=BE，求GC的长度．
哈尔滨市第六十九中学校2023－2024学年度下学期
八年级3月数学学科活动试卷答案
一、选择题（每小题3分，共30分）
二、填空题（每小题3分，共30分）
11．17 12． 13．29 14．13 15．（－3，5） 16．120
17．13 18． 19．4或14 20．
三、解答题（21、22题各7分，23、24题各8分，25、26、27题各10分）
21．（本题7分）
（1）（4分）图对3分（形状不唯一）对应所画平行四边形面积正确1分
（2）（3分）图对3分（两问平行四边形不标注顶点字母的各扣1分）
22．（本题7分）
证明：四边形ABCD是平行四边形，
∴AO=CO，BO=DO．
∵AE=CF，
∴AO－AE=CO－CF，即EO=FO．
又BO=DO，∴四边形BFDE是平行四边形
23．（本题8分）36步骤（1）勾股定理求AC=5（3分）步骤（2）勾股定理逆定理得Rt△ACD（3分）
步骤（3）得出面积36（2分）
24．（本题8分）
25．（本题10分）
（1）（3分）AG为Rt△ADE斜边中线得，通过导角得证．
（2）（3分）通过△AFD≌△BFE得AD=BE=m
（3）（4分）Rt△AED中勾股得出
26．（本题10分）
（1）（3分）导角得证
（2）（3分）24
（3）（4分）28
27．（本题10分）
（1）（2分）（2，0）
（2）（3分）d=t+2
（3）（5分）
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
C
D
D
D
D
B
C
C