2024九年级数学下学期期中学情评估试卷（附解析湘教版）

这是一份2024九年级数学下学期期中学情评估试卷（附解析湘教版），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．行驶在水平路面上的汽车，若把路看成直线，则此时转动的车轮与地面的位置关系是( )
A．相交 B．相切
C．相离 D．不确定
2．若将函数y＝－9x2的图象向左平移2个单位，再向上平移5个单位，得到的抛物线的表达式是( )
A．y＝－9(x＋2)2－5
B．y＝－9(x－2)2－5
C．y＝－9(x＋2)2＋5
D．y＝－9(x－2)2＋5
3．如图，AB是⊙O的弦，OC⊥AB于点C，连接OB，P是半径OB上一点，连接AP，若OB＝5，OC＝3，则AP的长不可能是( )
A．6 B．7 C．8 D．9
(第3题) (第5题)
4．下列关于抛物线y＝(x＋2)2＋6的说法正确的是( )
A．开口向下
B．顶点坐标为(2，6)
C．对称轴是直线x＝2
D．与y轴的交点为(0，10)
5．如图，一个底部呈球形的烧瓶，球的半径为5 cm，瓶内液体的最大深度CD＝2 cm，则截面圆中弦AB的长为( )
A．4 cm B．6 cm C．8 cm D．10 cm
6．已知二次函数y＝－x2－2mx－m2＋m＋2(m为常数)的图象与x轴有两个交点，则m的取值范围是( )
A．m－2 D．m≤－2
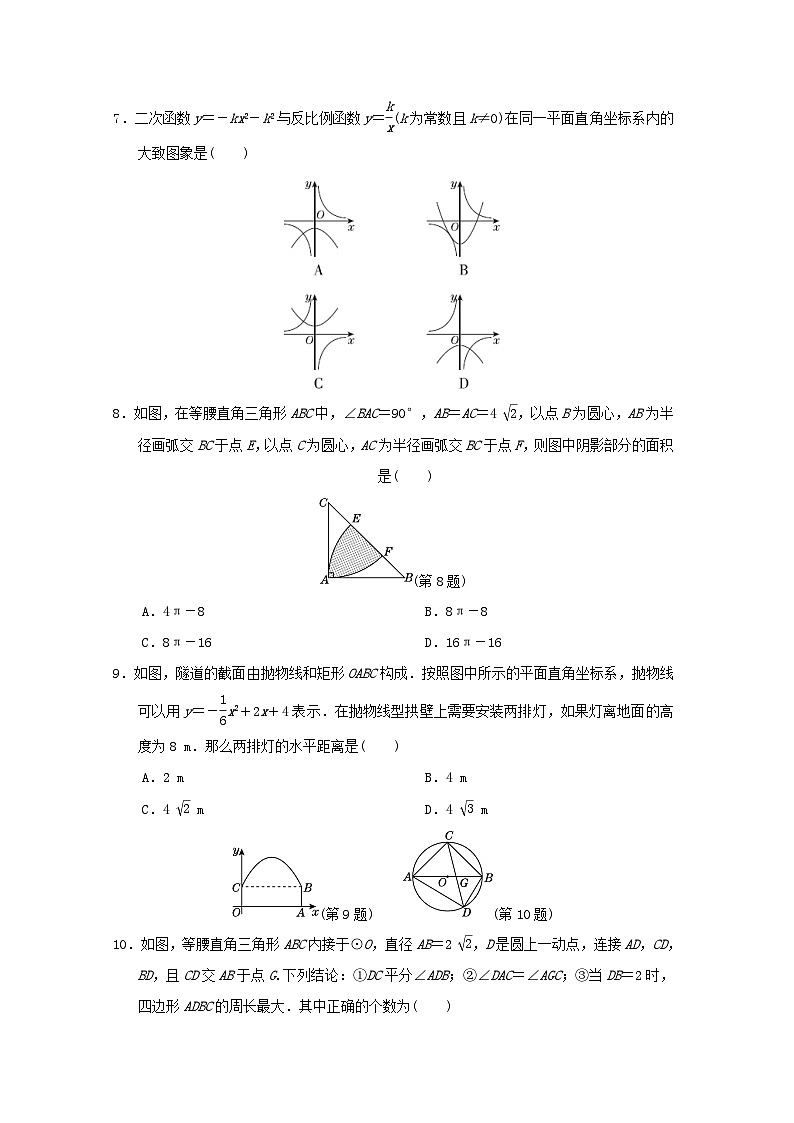
7．二次函数y＝－kx2－k2与反比例函数y＝eq \f(k,x)(k为常数且k≠0)在同一平面直角坐标系内的大致图象是( )
8．如图，在等腰直角三角形ABC中，∠BAC＝90°，AB＝AC＝4 eq \r(2)，以点B为圆心，AB为半径画弧交BC于点E，以点C为圆心，AC为半径画弧交BC于点F，则图中阴影部分的面积是( )
(第8题)
A．4π－8 B．8π－8
C．8π－16 D．16π－16
9．如图，隧道的截面由抛物线和矩形OABC构成．按照图中所示的平面直角坐标系，抛物线可以用y＝－eq \f(1,6)x2＋2x＋4表示．在抛物线型拱壁上需要安装两排灯，如果灯离地面的高度为8 m．那么两排灯的水平距离是( )
A．2 m B．4 m
C．4 eq \r(2) m D．4 eq \r(3) m
(第9题) (第10题)
10．如图，等腰直角三角形ABC内接于⊙O，直径AB＝2 eq \r(2)，D是圆上一动点，连接AD，CD，BD，且CD交AB于点G.下列结论：①DC平分∠ADB；②∠DAC＝∠AGC；③当DB＝2时，四边形ADBC的周长最大．其中正确的个数为( )
A．0 B．1 C．2 D．3
二、填空题(每题3分，共18分)
11．已知y＝(m－1)x|m|＋1＋2x－3是二次函数，则m的值为________．
12．如图，AB，AC，BC是⊙O的弦，连接OA.若AB＝OA，则∠C＝________．
(第12题) (第14题)
13．已知点M(－1，2)和点N都在抛物线y＝x2－2x＋c上，如果MN∥x轴，则线段MN的长度为________．
14．如图，△ABC中，AB＝AC，点O是BC边上一点，以点O为圆心，OB为半径作⊙O与边AC相切于点A，若BC＝9，则弦AB的长为________．
15．如图，已知eq \(AB,\s\up8(︵))与eq \(CD,\s\up8(︵))是公路弯道的外、内边线，它们有共同的圆心O，所对的圆心角都是72°，A，C，O在同一直线上，公路宽AC＝20 m，则弯道外边线比内边线多________m(结果保留π)．
(第15题) (第16题)
16．已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，则下列结论：①ac＞0；②b＝2a；③3a＋c＞0；④a＋c＞b＋2；⑤x＝5和x＝－7时函数值相等，其中正确的是________(填序号)．
三、解答题(第17～18题每题6分，第19～21题每题8分，第22题10分，第23题12分，第24题14分，共72分)
17．已知抛物线的顶点坐标是(2，1)，且该抛物线经过点(3，3)．求该抛物线的表达式．
18．如图，已知二次函数y＝x2－4x＋3的图象与坐标轴分别交于点A，B与C.
(1)求点A，B，C的坐标；
(2)直接写出当函数值y＜0时，自变量x的取值范围．
(第18题)
19．如图，⊙O的直径AB＝20，弦AC＝12，∠ACB的平分线交⊙O于点D，求BC，AD，BD的长．
(第19题)
20．如图，四边形ABCD是⊙O的内接四边形，BC是⊙O的直径，∠ACB＝30°，AB＝2，点D为eq \(AC,\s\up8(︵))的中点．
(第20题)
(1)求⊙O的半径；
(2)求∠DAC的度数．
21．如图，正五边形ABCDE的边长为6，以点B为圆心，线段AB为半径画圆．
(1)求∠ACB的度数；
(2)求eq \(AC,\s\up8(︵))的长度．
(第21题)
22．某商店经销一种双肩包，已知这种双肩包的成本价为每个30元，市场调查发现，这种双肩包每天的销售量y(个)与销售单价x(元)有如下关系：y＝－x＋60(30≤x≤60)．设这种双肩包每天的销售利润为w元．
(1)求w与x之间的函数表达式；
(2)当这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
(3)如果物价部门规定这种双肩包的销售单价不得高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少元？
23．如图，AC是⊙O的直径，P为eq \(AC,\s\up8(︵))的中点，连接AP并延长至点B，使PB＝AP，连接CP，CB，OP.
(第23题)
(1)求证：BC为⊙O的切线；
(2)若AC＝4，求图中阴影部分的面积．
24．已知抛物线y＝－x2＋bx＋c经过点A(0，－5)和点B(3，－2)．
(1)求抛物线的表达式；
(2)若⊙P的半径为1，圆心P在抛物线上运动，⊙P在运动过程中，是否存在与坐标轴相切的情况？若存在，请求出圆心P的坐标；若不存在，请说明理由；
(3)若⊙Q的半径为r，圆心Q在抛物线上，当⊙Q与两坐标轴都相切时，求半径r.
答案
一、1. B 2. C 3. D 4. D 5. C 6. C 7. A 8. C
9. D 点拨：y＝－eq \f(1,6)x2＋2x＋4＝－eq \f(1,6)(x－6)2＋10.当y＝8时，8＝－eq \f(1,6)(x－6)2＋10，解得x1＝6＋2 eq \r(3)，x2＝6－2 eq \r(3).则x1－x2＝4 eq \r(3).所以两排灯的水平距离是4 eq \r(3) m.
10. D
二、11. －1
12. 30° 点拨：连接OB，由AB＝OA＝OB可知△OAB是等边三角形，∴∠O＝60°，∴∠C＝30°.
13. 4
14. 3 eq \r(3) 点拨：如图，连接OA.
(第14题)
∵AB＝AC，∴∠B＝∠C.
∵OA＝OB，∴∠OAB＝∠B.
∵AC是⊙O的切线，
∴OA⊥AC，即∠OAC＝90°，
∴∠B＋∠C＋∠OAB＝90°，
∴∠C＝30°，
∴OA＝eq \f(1,2)OC＝OB.
∵BC＝9，∴OB＋OC＝OB＋2OB＝9，
∴OB＝OA＝3，∴OC＝6，
∴AB＝AC＝eq \r(OC2－OA2)＝3 eq \r(3).
15. 8π
16. ②④⑤ 点拨：因为抛物线开口向下，所以a＜0.
因为抛物线与y轴的交点在x轴上方，
所以c＞0，所以ac＜0，所以①错误；
因为抛物线的对称轴为直线x＝－eq \f(b,2a)＝－1，
所以b＝2a，所以②正确；
当x＝1时，a＋b＋c＝3a＋c，由图象得3a＋c＜0，
所以③错误；
因为抛物线的对称轴为直线x＝－1，
所以x＝－1时，y最大，即a－b＋c＞2，
所以a＋c＞b＋2，所以④正确；
因为抛物线的对称轴为直线x＝－1，
所以x＝5和x＝－7时函数值相等，所以⑤正确．
三、17. 解：因为抛物线的顶点坐标是(2，1)，
所以设该抛物线的表达式为y＝a(x－2)2＋1.
因为该抛物线经过点(3，3)，
所以3＝a×(3－2)2＋1，解得a＝2.
所以该抛物线的表达式是y＝2(x－2)2＋1.
18. 解：(1)令y＝0，则x2－4x＋3＝0.
解得x1＝1，x2＝3.由题图可知点A在点B的右侧，
所以点A的坐标为(3，0)，点B的坐标为(1，0)．
当x＝0时，y＝3，所以点C的坐标为(0，3)．
(2)当函数值y＜0时，自变量x的取值范围为1＜x＜3.
19. 解：∵AB是⊙O的直径，
∴∠ADB＝∠ACB＝90°，
∴在Rt△ABC中，BC＝eq \r(AB2－AC2)＝16.
∵CD是∠ACB的平分线，
∴∠ACD＝∠DCB＝45°.
∵∠DBA＝∠ACD，∠DAB＝∠DCB，
∴∠DBA＝∠DAB＝45°，
∴AD＝BD.
在Rt△ABD中，sin ∠DBA＝sin 45°＝eq \f(AD,AB)，
∴AD＝eq \f(\r(2),2)×AB＝10 eq \r(2)，
∴AD＝BD＝10 eq \r(2).
20. 解：(1)∵BC为⊙O的直径，
∴∠BAC＝90°.
∵∠ACB＝30°，AB＝2，
∴BC＝2AB＝4，
∴⊙O的半径为2.
(2) ∵四边形ABCD为⊙O的内接四边形，
∴∠B＋∠D＝180°.
∵∠B＝90°－30°＝60°，
∴∠D＝120°.
∵点D为eq \(AC,\s\up8(︵))的中点，
∴eq \(AD,\s\up8(︵))＝eq \(CD,\s\up8(︵))，
∴∠DCA＝∠DAC，
∴∠DAC＝eq \f(180°－∠D,2)＝30°.
21. 解：(1)∵五边形ABCDE是正五边形，
∴AB＝BC＝CD＝DE＝EA，
∠B＝∠BCD＝∠D＝∠E＝∠BAE.
∵正五边形ABCDE的内角和为180°×(5－2)＝540°，
∴∠B＝eq \f(540°,5)＝108°.
∵AB＝BC，
∴∠ACB＝∠BAC.
∴∠ACB＝(180°－108°)÷2＝36°.
(2)∵正五边形ABCDE的边长为6，
∴⊙B的半径AB＝6.
又∵∠B＝108°，
∴eq \(AC,\s\up8(︵))的长度为eq \f(108π×6,180)＝eq \f(18π,5).
22. 解：(1)由题意得w＝(x－30)·y＝(x－30)(－x＋60)＝－x2＋30x＋60x－1 800＝－x2＋90x－1 800，
即w与x之间的函数表达式为w＝－x2＋90x－1 800.
(2)由(1)知w＝－x2＋90x－1 800＝－(x－45)2＋225.
因为－1＜0，所以当x＝45时，w取得最大值，最大值是225.
答：当这种双肩包销售单价定为45元时，每天的销售利润最大，最大利润是225元．
(3)当w＝200时，－x2＋90x－1 800＝200，
解得x1＝40，x2＝50(不符合题意，舍去)．
答：销售单价应定为40元．
23. (1)证明：∵AC是⊙O的直径，
∴∠APC＝90°，
∴∠BPC＝90°.
∵P为eq \(AC,\s\up8(︵))的中点，
∴eq \(AP,\s\up8(︵))＝eq \(CP,\s\up8(︵))，
∴AP＝CP，
∴∠PAC＝∠PCA＝45°.
∵PB＝AP，
∴PC＝PB，
∴∠PCB＝∠PBC＝45°，
∴∠ACB＝∠PCA＋∠PCB＝90°，
∴AC⊥BC，
∴BC为⊙O的切线．
(2)解：∵∠PAC＝∠PBC＝45°，AC＝4，
∴BC＝AC＝4，OA＝OP＝2.
∵PC＝AP，OA＝OC，∴AC⊥OP，
∴S阴影＝S△ABC－S△AOP－S扇形OPC
＝eq \f(1,2)×4×4－eq \f(1,2)×2×2－eq \f(90π×22,360)＝6－π.
24. 解：(1)由题意，得eq \b\lc\{(\a\vs4\al\c1(c＝－5，,－9＋3b＋c＝－2，))
解得eq \b\lc\{(\a\vs4\al\c1(c＝－5，,b＝4.))
所以抛物线的表达式为y＝－x2＋4x－5.
(2)存在．设P(x，y)，①由⊙P与x轴相切得 y＝±1.
当y＝1时，－x2＋4x－5＝1，方程无实数解．
当y＝－1时，－x2＋4x－5＝－1，解得x1＝x2＝2，
所以当⊙P与x轴相切时，圆心P的坐标为(2，－1)．
②由⊙P与y轴相切得x＝±1.当x＝1时，y＝－1＋4－5＝－2，即圆心P的坐标为(1，－2)．
当x＝－1时，y＝－1－4－5＝－10，即圆心P的坐标为(－1，－10)．所以当⊙P与y轴相切时，圆心P的坐标为(1，－2)或(－1，－10)．综上，圆心P的坐标为(2，－1)，(1，－2)或(－1，－10)．
(3)由题意，得圆心Q(r, －r2＋4r－5)，由⊙Q与两坐轴都相切，得－r2＋4r－5＝r①或－r2＋4r－5＝－r②.①无解，②解得r1＝eq \f(5＋\r(5),2)，r2＝eq \f(5－\r(5),2)，所以⊙Q与两坐标轴都相切时，半径r为eq \f(5＋\r(5),2)或eq \f(5－\r(5),2).