




2024年四川省凉山州会东县中考数学一诊模拟试题(原卷版+解析版)
展开1. 下列方程中,关于的一元二次方程是( )
A. B. C. D.
2. 下列四个几何体中,左视图是矩形的是( )
A. B. C. D.
3. 下列关于抛物线的判断中,错误的是( )
A. 形状与抛物线相同B. 对称轴是直线
C. 当时,y随x的增大而减小D. 当时,
4. 如图,《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著,该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽,每株脚钱三文足,无钱准与一株椽.”大意是:现请人代买一批椽,这批椽的价钱为6210文,如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?(椽,装于屋顶以支持屋顶材料的木杆)设这批椽有x株,则符合题意的方程是( )
A. B. C. D.
二、填空题:本题共7小题,共30分。
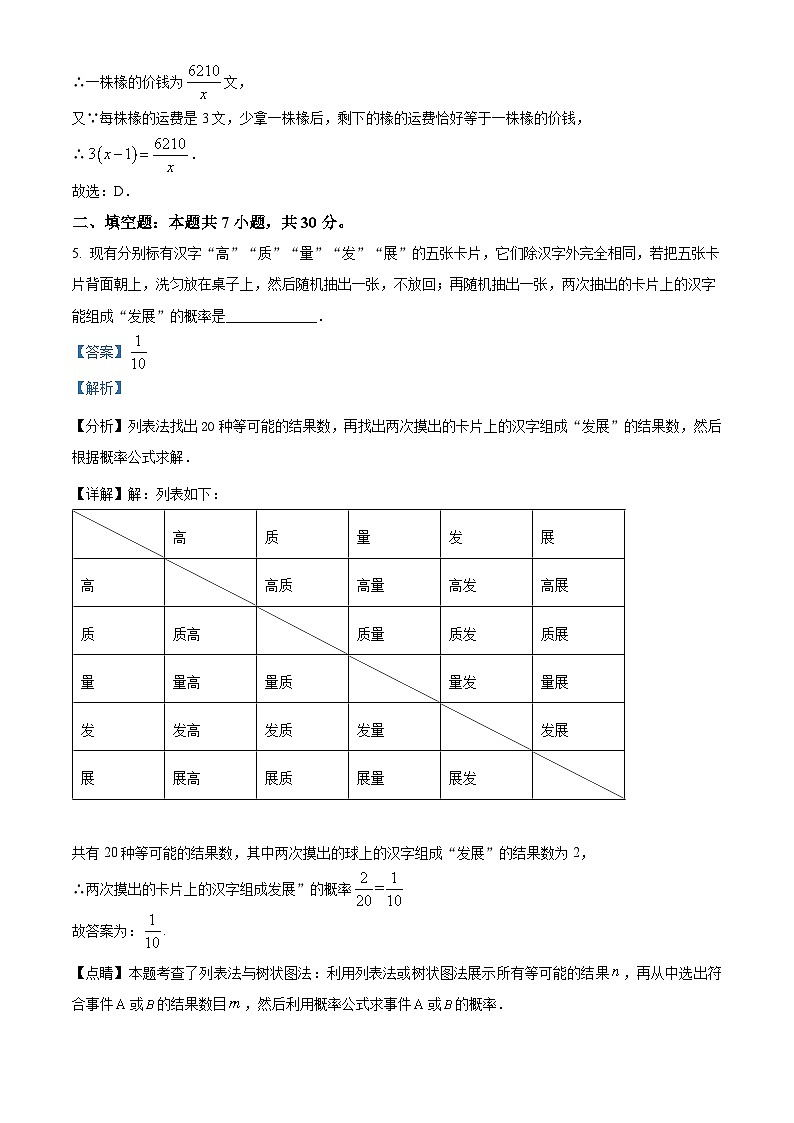
5. 现有分别标有汉字“高”“质”“量”“发”“展”的五张卡片,它们除汉字外完全相同,若把五张卡片背面朝上,洗匀放在桌子上,然后随机抽出一张,不放回;再随机抽出一张,两次抽出的卡片上的汉字能组成“发展”的概率是_____________.
6. 若有意义,则一次函数的图像经过第______象限.
7. 如图,过作轴,轴,点都在直线上,若双曲线与总有公共点,则k的取值范围是______.
8. 如图,直线,与分别相切于点,,为上一点,且,则的度数是______.
9. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若AB=,则CD=_____.
10. 如图,点F是正方形ABCD内一点,DF=DC,连接CF并延长交AB边于点E,EGBC交DF于点G,若EG=3,GF=1,则正方形ABCD的面积为_________.
11. 如图,正方形ABCD中,AB=2,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.
三、解答题:本题共9小题,共104分。
12. 解方程
(1)
(2)
13. 在学习解直角三角形以后,某班数学兴趣小组的同学测量了旗杆的高度,如图,某一时刻,旗杆的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长为6米,落在斜坡上的影长为4米,,点、、三点共线,且,同一时刻,光线与旗杆的夹角为,斜坡的坡比为,
(1)求坡角的度数;
(2)旗杆的高度为多少米?(结果保留根号)
14. 爱动脑筋的小明在做二次根式的化简时,发现一些二次根式的被开方数是二次三项式,而且这些二次三项式正好是完全平方式的结构,于是就可以利用二次根式的性质:来进一步化简.
比如:,
∴当即时,原式;当即时,原式.
(1)仿照上面的例子,请你尝试化简.
(2)判断甲、乙两人在解决问题:“,求的值”时谁的答案正确,并说明理由.
甲的答案:原式;
乙答案:原式.
(3)化简并求值:,其中.
15. 第31届世界大学生运动会将于2023年7月28日至8月8日在成都举行,某校开展了“爱成都,迎大运”系列活动,增设篮球,足球,柔道,射击共四个课外活动项目.为了解全校1500名同学对增设的四个活动项目的喜爱情况,在全校范围内随机抽取了若干名同学,对他们喜爱的项目(每人限选一项)进行了问卷调查,将数据进行了统计,并绘制成了如图所示的条形统计图和扇形统计图,请回答下列问题:
(1)参加问卷调查的同学共 名,补全条形统计图;
(2)估计该校1500名同学中喜爱篮球运动的人数;
(3)学校准备组建一支校篮球队,某班甲,乙,丙,丁四名同学平时都很喜欢篮球运动,现决定从这四人中任选两名同学加入球队,请你用树状图或列表法求恰好选中甲,乙两名同学概率.
16. 如图,在中,,以为直径作,交于,过作,交于.
(1)求证:是的切线;
(2)连接,如果半径为,,求的长;
(3)在(2)的条件下,求的面积.
17. 随旅游业的快速发展,外来游客对住宿的需求明显增大,某宾馆拥有的床位数不断增加.
(1)该宾馆床位数从2021年底的200个增长到2023年底的288个,求该宾馆这两年(从2021年底到2023年底)拥有的床位数的年平均增长率;
(2)该宾馆打算向游客出售了一款纪念工艺品,每件成本50元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是100元时,每天销售量是50件,若销售单价每降低1元,每天就可多售出5件。若该馆想要每天的销售利润达到4000元,且销量尽可能大,应该如何定价?
18. 在矩形中,点为射线上一动点,连接.
(1)当点在边上时,将沿翻折,使点恰好落在对角线上点处,交于点.
①如图,若,求度数;
②如图,当,且时,求的长.
(2)当点在的延长线上时,当,时将矩形沿进行翻折,点的对应点为,当点,,三点共线时,求的长.
19. 如图,为的弦,点C为的中点,的延长线交于点D,连接,过点D作的切线交的延长线于点E.
(1)求证:;
(2)若的半径为3,,求的长.
20. 如图,抛物线与轴交于点、两点,与轴交点,连接,抛物线的对称轴交轴于点,交于点,顶点为.
(1)求抛物线的解析式及顶点的坐标;
(2)若是直线上方抛物线上一动点,连接交于点,当的值最大时,求点的坐标;
(3)已知点是抛物线上的一点,连接,若,求点的坐标.
2024年四川省成都市中考一诊考试数学模拟预测题(原卷版+解析版): 这是一份2024年四川省成都市中考一诊考试数学模拟预测题(原卷版+解析版),文件包含2024年四川省成都市中考一诊考试数学模拟预测题原卷版docx、2024年四川省成都市中考一诊考试数学模拟预测题解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
2024年四川省凉山州会东县中考数学一诊试卷(含解析): 这是一份2024年四川省凉山州会东县中考数学一诊试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024年山东德州中考数学一模模拟试题(原卷版+解析版): 这是一份2024年山东德州中考数学一模模拟试题(原卷版+解析版),文件包含精品解析2024年山东德州中考数学一模模拟试题原卷版docx、精品解析2024年山东德州中考数学一模模拟试题解析版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。












