2024年河南省洛阳市西工区中考数学一模试卷

这是一份2024年河南省洛阳市西工区中考数学一模试卷，共24页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
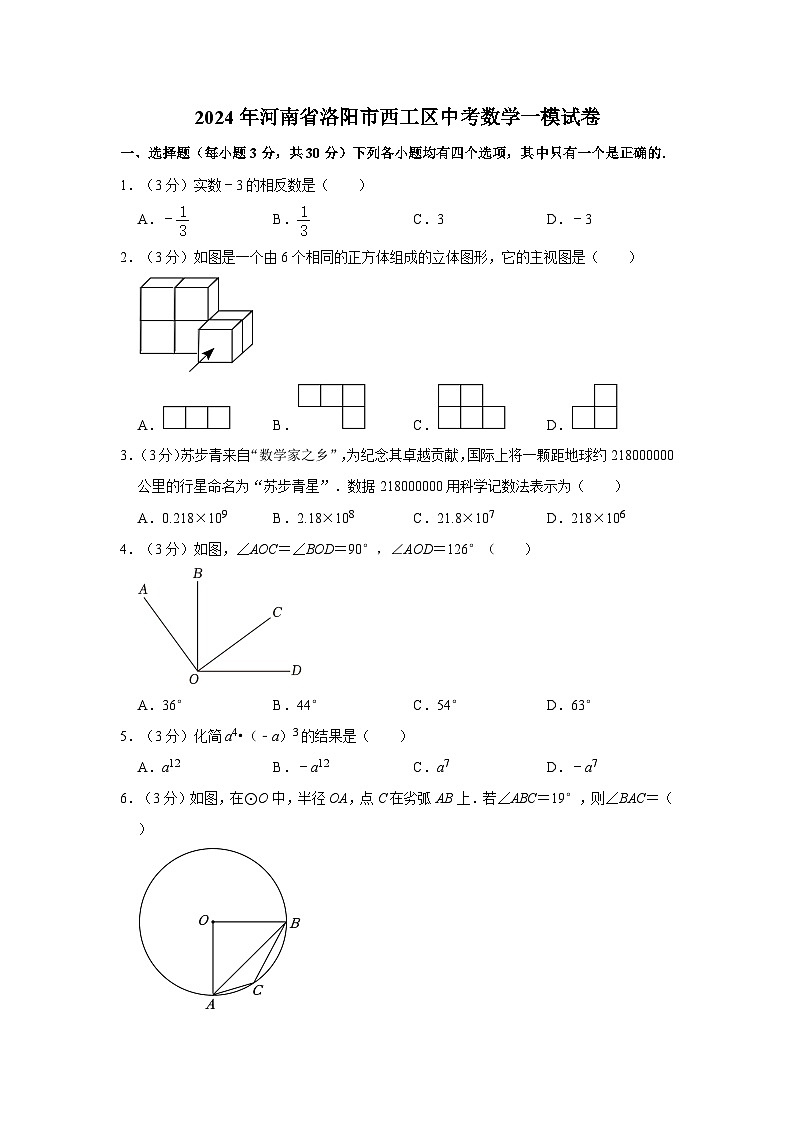
1．（3分）实数﹣3的相反数是（ ）
A．﹣B．C．3D．﹣3
2．（3分）如图是一个由6个相同的正方体组成的立体图形，它的主视图是（ ）
A．B．C．D．
3．（3分）苏步青来自“数学家之乡”，为纪念其卓越贡献，国际上将一颗距地球约218000000公里的行星命名为“苏步青星”．数据218000000用科学记数法表示为（ ）
A．0.218×109B．2.18×108C．21.8×107D．218×106
4．（3分）如图，∠AOC＝∠BOD＝90°，∠AOD＝126°（ ）
A．36°B．44°C．54°D．63°
5．（3分）化简a4•（﹣a）3的结果是（ ）
A．a12B．﹣a12C．a7D．﹣a7
6．（3分）如图，在⊙O中，半径OA，点C在劣弧AB上．若∠ABC＝19°，则∠BAC＝（ ）
A．30°B．26°C．25°D．20°
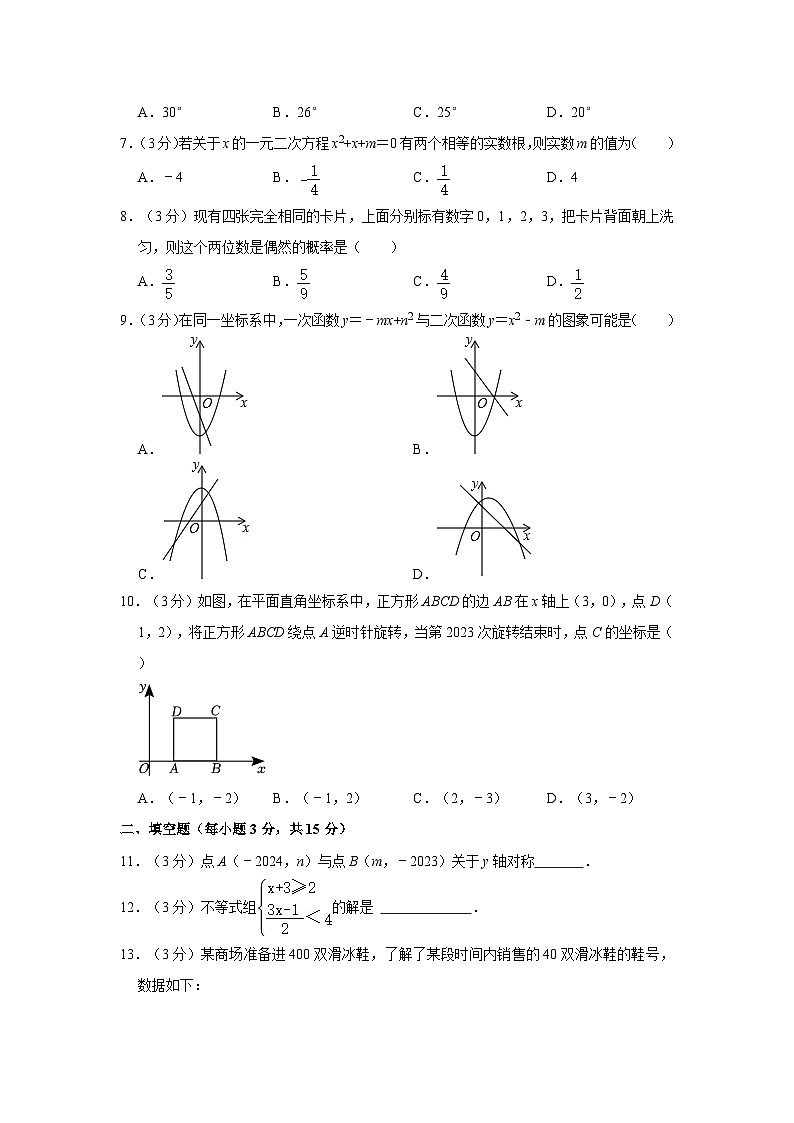
7．（3分）若关于x的一元二次方程x2+x+m＝0有两个相等的实数根，则实数m的值为（ ）
A．﹣4B．C．D．4
8．（3分）现有四张完全相同的卡片，上面分别标有数字0，1，2，3，把卡片背面朝上洗匀，则这个两位数是偶然的概率是（ ）
A．B．C．D．
9．（3分）在同一坐标系中，一次函数y＝﹣mx+n2与二次函数y＝x2﹣m的图象可能是（ ）
A．B．
C．D．
10．（3分）如图，在平面直角坐标系中，正方形ABCD的边AB在x轴上（3，0），点D（1，2），将正方形ABCD绕点A逆时针旋转，当第2023次旋转结束时，点C的坐标是（ ）
A．（﹣1，﹣2）B．（﹣1，2）C．（2，﹣3）D．（3，﹣2）
二、填空题（每小题3分，共15分）
11．（3分）点A（﹣2024，n）与点B（m，﹣2023）关于y轴对称 ．
12．（3分）不等式组的解是 ．
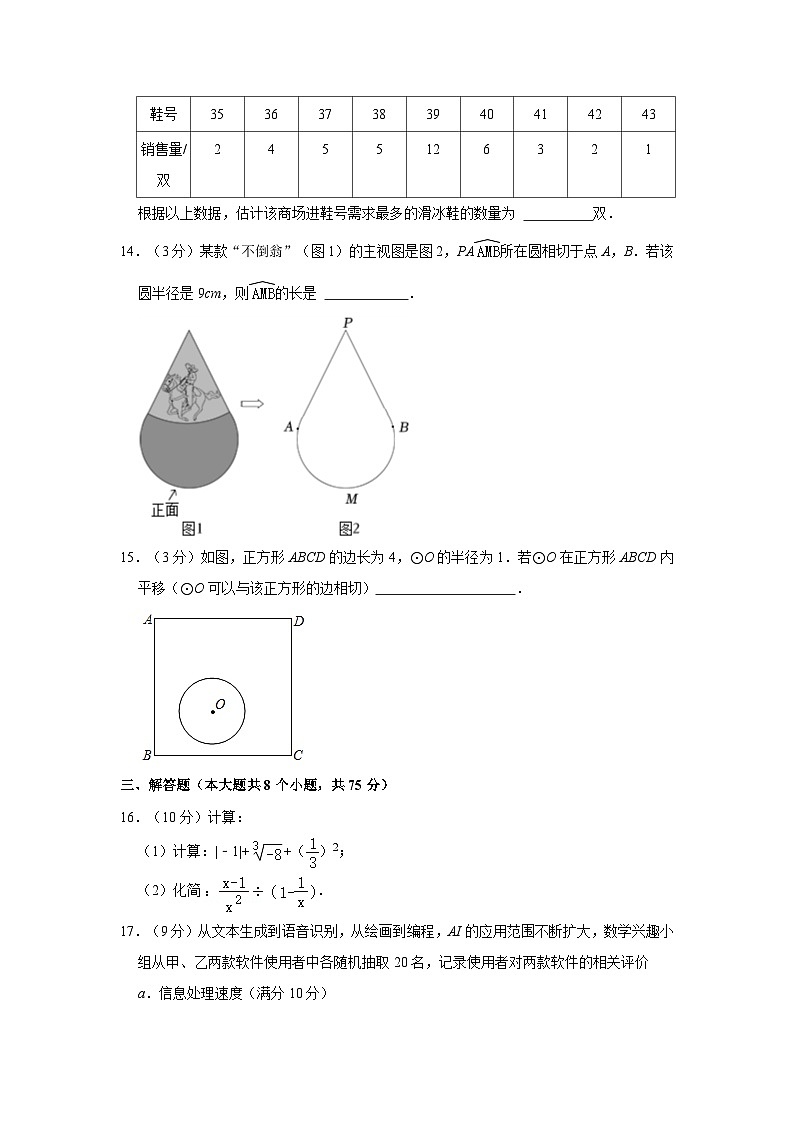
13．（3分）某商场准备进400双滑冰鞋，了解了某段时间内销售的40双滑冰鞋的鞋号，数据如下：
根据以上数据，估计该商场进鞋号需求最多的滑冰鞋的数量为 双．
14．（3分）某款“不倒翁”（图1）的主视图是图2，PA所在圆相切于点A，B．若该圆半径是9cm，则的长是 ．
15．（3分）如图，正方形ABCD的边长为4，⊙O的半径为1．若⊙O在正方形ABCD内平移（⊙O可以与该正方形的边相切） ．
三、解答题（本大题共8个小题，共75分）
16．（10分）计算：
（1）计算：|﹣1|++（）2；
（2）化简．
17．（9分）从文本生成到语音识别，从绘画到编程，AI的应用范围不断扩大，数学兴趣小组从甲、乙两款软件使用者中各随机抽取20名，记录使用者对两款软件的相关评价
a．信息处理速度（满分10分）
b．信息识别准确度（满分10分）
c．信息处理速度和信息识别准确度得分统计表
根据以上信息，解答下列问题：
（1）表格中a＝ ，b＝ ，S甲2 S乙2（填“＞”“＝”或“＜”）；
（2）若某市共有20.4万人使用甲款AI软件，请你估计对本款软件信息识别准确度打分超过7分的人数；
（3）综合上表中的统计量，你认为哪款AI软件使用效果更好？请说明理由（列出两条即可）．
18．（9分）如图，已知AB＝AC，AD＝AE
（1）求证：△ABD≌△ACE；
（2）判断△BOC的形状，并说明理由．
19．（9分）如图，一次函数的图象与反比例函数（﹣1，2），与x轴交于点B．
（1）a的值为 ，k的值为 ．
（2）请用无刻度的直尺和圆规，过点A作AC⊥AB，交x轴于点C．（要求：不写作法，保留作图痕迹）
（3）求点C的坐标．
20．（9分）图1是某款自动旋转圆形遮阳伞，伞面完全张开时张角呈180°，图2是其侧面示意图．已知支架AB长为2.6米，悬托架AE＝DE＝0.5米，点E固定在伞面上，点D，E，F始终共线．为实现遮阳效果最佳；自动调整手柄D沿着AB移动，以保证太阳光线与DF始终垂直．某一时刻测得BD＝2米．请求出此时遮阳伞影子中GH的长度．
21．（9分）研学旅行继承和发展了我国传统游学、“读万卷书，行万里路”的教育理念和人文精神，成为素质教育的新内容和新方式．疫情散去，某中学组织七年级的10名教师和410名学生赴安阳市参观殷墟博物馆和中国文字博物馆．下面是李老师和刘老师有关租车问题的对话：
李老师：“某客运公司有A，B两种型号的客车对外出租，每辆A型客车比每辆B型客车多坐15名师生，若租用相同数量的B型客车将有105名师生无座可坐”．
刘老师：“A型客车每辆每天的租金比B型客车高150元．八年级师生上周在这个客运公司租了4辆A型客车和2辆B型客车到这两个地方，一天的租金共计5100元．”
根据以上对话，解答下列问题：
（1）每辆A型客车和B型客车可坐师生的人数分别是多少？
（2）该客运公司A型客车和B型客车每辆每天的租金分别是多少元？
（3）若同时租用两种客车，要使每位师生都有座位，且每辆客车恰好坐满
22．（10分）如图，抛物线y＝ax2+bx（a≠0）过点A（4，0），点B是抛物线上一个动点，使边CD在x轴上（点C在点D的左侧），点E在抛物线上，当时，．
（1）求抛物线的解析式；
（2）当m为何值时，四边形BCDE是正方形？
23．（10分）综合与实践：
综合与实践课上，老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动．
（1）操作判断：
如图1，先用对折的方式确定矩形ABCD的边AB的中点E，再沿DE折叠，把纸片展平，延长DF
请写出线段FG与线段BG的数量关系 ；
（2）迁移思考：
如图2，把▱ABCD按照（1）中的操作进行折叠和作图，BG这两条线段之间的数量关系，并仅就图2证明你的判断．
（3）拓展探索：
如图1，若AB＝2，按照（1），请直接写出当CG＝1时AD的值．
参考答案与试题解析
一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的．
1．（3分）实数﹣3的相反数是（ ）
A．﹣B．C．3D．﹣3
【解答】解：﹣3的相反数是3，
故选：C．
2．（3分）如图是一个由6个相同的正方体组成的立体图形，它的主视图是（ ）
A．B．C．D．
【解答】解：从正面看，一共有三列、2、1．
故选：C．
3．（3分）苏步青来自“数学家之乡”，为纪念其卓越贡献，国际上将一颗距地球约218000000公里的行星命名为“苏步青星”．数据218000000用科学记数法表示为（ ）
A．0.218×109B．2.18×108C．21.8×107D．218×106
【解答】解：218000000＝2.18×108．
故选：B．
4．（3分）如图，∠AOC＝∠BOD＝90°，∠AOD＝126°（ ）
A．36°B．44°C．54°D．63°
【解答】解：∵∠AOC＝90°，∠AOD＝126°，
∴∠COD＝∠AOD﹣∠AOC＝36°，
∵∠BOD＝90°，
∴∠BOC＝∠BOD﹣∠COD
＝90°﹣36°
＝54°．
故选：C．
5．（3分）化简a4•（﹣a）3的结果是（ ）
A．a12B．﹣a12C．a7D．﹣a7
【解答】解：a4•（﹣a）3＝﹣a3．
故选：D．
6．（3分）如图，在⊙O中，半径OA，点C在劣弧AB上．若∠ABC＝19°，则∠BAC＝（ ）
A．30°B．26°C．25°D．20°
【解答】解：连接OC，
∵∠ABC＝19°，
∴∠AOC＝2∠ABC＝38，
∵半径OA，OB互相垂直，
∴∠AOB＝90°，
∴∠BOC＝90°﹣38＝52，
∴，
故选：B．
7．（3分）若关于x的一元二次方程x2+x+m＝0有两个相等的实数根，则实数m的值为（ ）
A．﹣4B．C．D．4
【解答】解：根据题意得Δ＝12﹣7m＝0，
解得m＝．
故选：C．
8．（3分）现有四张完全相同的卡片，上面分别标有数字0，1，2，3，把卡片背面朝上洗匀，则这个两位数是偶然的概率是（ ）
A．B．C．D．
【解答】解：画树状图得：
∵共有9种等可能的结果，这个两位数是偶数的有5种情况，
∴这个两位数是偶数的概率是：，
故选：B．
9．（3分）在同一坐标系中，一次函数y＝﹣mx+n2与二次函数y＝x2﹣m的图象可能是（ ）
A．B．
C．D．
【解答】解：∵二次函数y＝x2﹣m中1＞4，
∴二次函数图象开口向上，C、D选项不符合题意，
∴﹣m＜0，
∴一次函数y＝﹣mx+n2经过第一、二、四象限．
故选：B．
10．（3分）如图，在平面直角坐标系中，正方形ABCD的边AB在x轴上（3，0），点D（1，2），将正方形ABCD绕点A逆时针旋转，当第2023次旋转结束时，点C的坐标是（ ）
A．（﹣1，﹣2）B．（﹣1，2）C．（2，﹣3）D．（3，﹣2）
【解答】解：由题可知，将正方形ABCD绕点A逆时针旋转，
∴每旋转4次则回到原位置，
∵2023÷4＝505……3，
∴第2023次旋转结束后，图形顺时针旋转了90°，
∵点B（3，0），5），
∴C（3，2），
∴第2023次旋转结束时，点C的坐标是（4，
故选：D．
二、填空题（每小题3分，共15分）
11．（3分）点A（﹣2024，n）与点B（m，﹣2023）关于y轴对称 1 ．
【解答】解：∵点A（﹣2024，n）与点B（m，
∴n＝﹣2023，m＝2024，
∴n+m＝﹣2023+2024＝1．
故答案为：1．
12．（3分）不等式组的解是 ﹣1≤x＜3 ．
【解答】解：，
解不等式①，得：x≥﹣1，
解不等式②，得：x＜3，
∴该不等式组的解集为﹣8≤x＜3，
故答案为：﹣1≤x＜5．
13．（3分）某商场准备进400双滑冰鞋，了解了某段时间内销售的40双滑冰鞋的鞋号，数据如下：
根据以上数据，估计该商场进鞋号需求最多的滑冰鞋的数量为 120 双．
【解答】解：根据统计表可得，39号的鞋卖的最多，
则估计该商场进鞋号需求最多的滑冰鞋的数量为（双）．
故答案为：120．
14．（3分）某款“不倒翁”（图1）的主视图是图2，PA所在圆相切于点A，B．若该圆半径是9cm，则的长是 11πcm ．
【解答】解：OA⊥PA，OB⊥PB，OB交于点O，
∴∠OAP＝∠OBP＝90°，
∵∠P＝40°，
∴∠AOB＝140°，
∴优弧AMB对应的圆心角为360°﹣140°＝220°，
∴优弧AMB的长是：＝11π（cm），
故答案为：11πcm．
15．（3分）如图，正方形ABCD的边长为4，⊙O的半径为1．若⊙O在正方形ABCD内平移（⊙O可以与该正方形的边相切） 3+1 ．
【解答】解：当⊙O与CB、CD相切时，如图，
过O点作OE⊥BC于E，OF⊥CD于F，
∴OE＝OF＝1，
∴OC平分∠BCD，
∵四边形ABCD为正方形，
∴点O在AC上，
∵AC＝BC＝6OE＝，
∴AQ＝OA+OQ＝4﹣+1＝3，
即点A到⊙O上的点的距离的最大值为3+4，
故答案为3+6．
三、解答题（本大题共8个小题，共75分）
16．（10分）计算：
（1）计算：|﹣1|++（）2；
（2）化简．
【解答】解：（1）|﹣1|++（）8
＝1+（﹣2）+
＝﹣1+
＝﹣；
（2）÷（4﹣）
＝÷
＝
＝．
17．（9分）从文本生成到语音识别，从绘画到编程，AI的应用范围不断扩大，数学兴趣小组从甲、乙两款软件使用者中各随机抽取20名，记录使用者对两款软件的相关评价
a．信息处理速度（满分10分）
b．信息识别准确度（满分10分）
c．信息处理速度和信息识别准确度得分统计表
根据以上信息，解答下列问题：
（1）表格中a＝ 7.5 ，b＝ 9 ，S甲2 ＜ S乙2（填“＞”“＝”或“＜”）；
（2）若某市共有20.4万人使用甲款AI软件，请你估计对本款软件信息识别准确度打分超过7分的人数；
（3）综合上表中的统计量，你认为哪款AI软件使用效果更好？请说明理由（列出两条即可）．
【解答】解：（1）共20个数据，乙组数据第10个、8，
所以中位数a＝＝7.4，
甲组数据中9出现的次数最多，
故b＝9，
由信息识别准确度的折线图可知，S甲4＜S乙2．
故答案为：7.4，9，＜；
（2）204000×＝51000（人），
估计对本款软件信息识别准确度打分超过6分的人数为51000人；
（3）甲款AI软件使用效果更好（答案不唯一），理由如下：
∵信息识别准确度得分的平均数甲高于乙，而且甲的方差小于乙的方差，
∴甲更稳定，
∴甲款AI软件使用效果更好．
18．（9分）如图，已知AB＝AC，AD＝AE
（1）求证：△ABD≌△ACE；
（2）判断△BOC的形状，并说明理由．
【解答】证明：（1）∵AB＝AC，∠BAD＝∠CAE，
∴△ABD≌△ACE（SAS）；
（2）△BOC是等腰三角形，
理由如下：
∵△ABD≌△ACE，
∴∠ABD＝∠ACE，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠ABC﹣∠ABD＝∠ACB﹣∠ACE，
∴∠OBC＝∠OCB，
∴BO＝CO，
∴△BOC是等腰三角形．
19．（9分）如图，一次函数的图象与反比例函数（﹣1，2），与x轴交于点B．
（1）a的值为 ，k的值为 ﹣2 ．
（2）请用无刻度的直尺和圆规，过点A作AC⊥AB，交x轴于点C．（要求：不写作法，保留作图痕迹）
（3）求点C的坐标．
【解答】解：（1）把A（﹣1，2）代入，得，
解得：；
把A（﹣1，3）代入，得，
解得：k＝﹣2．
故答案为：；﹣2；
（2）如图所示，直线AC即为所作；
（3）由（1）知：一次函数解析式为：，
令y＝6，则，
解得：x＝3，
∴B（3，0），
∴OB＝7，
过点A作AD⊥x轴于D，
∵A（﹣1，2），
∴AD＝6，OD＝1，
∴BD＝4，
∵AD⊥x轴，
∴∠ADC＝∠BDA＝90°，
∴∠ABD+∠BAD＝90°，
∵AC⊥AB，
∴∠BAD+∠CAD＝∠BAC＝90°，
∴∠ABD＝∠CAD，
∴△ABD∽△CAD，
∴，即，
∴CD＝2，
∴OC＝2，
∵点C在x轴的负半轴上，
∴C（﹣2，3）．
20．（9分）图1是某款自动旋转圆形遮阳伞，伞面完全张开时张角呈180°，图2是其侧面示意图．已知支架AB长为2.6米，悬托架AE＝DE＝0.5米，点E固定在伞面上，点D，E，F始终共线．为实现遮阳效果最佳；自动调整手柄D沿着AB移动，以保证太阳光线与DF始终垂直．某一时刻测得BD＝2米．请求出此时遮阳伞影子中GH的长度．
【解答】解：如图，过点G作GM⊥FH于点M，
∵AB＝2.5米，AD＝7米，
∴AD＝2.6﹣2＝0.6（米），
∵AE＝DE＝7.5米，EN⊥AB，
∴DN＝AN＝AD＝0.3米，
在Rt△DEN中，DN＝2.3米，
∴EN＝＝0.4（米），
∵∠α+∠MGH＝90°，∠MGH+∠BGD＝180°﹣90°＝90°，∠BDG+∠NDG＝180°﹣90°＝90°，
∴∠α＝∠NDE，
在Rt△DEN中，sin∠NDE＝＝，
在Rt△HGM中，sin∠α＝＝，
∵GM＝DF＝0.5×8＝2（米），
∴＝，
∴GH＝2.6，
即此时遮阳伞影子中GH的长度为2.5米．
21．（9分）研学旅行继承和发展了我国传统游学、“读万卷书，行万里路”的教育理念和人文精神，成为素质教育的新内容和新方式．疫情散去，某中学组织七年级的10名教师和410名学生赴安阳市参观殷墟博物馆和中国文字博物馆．下面是李老师和刘老师有关租车问题的对话：
李老师：“某客运公司有A，B两种型号的客车对外出租，每辆A型客车比每辆B型客车多坐15名师生，若租用相同数量的B型客车将有105名师生无座可坐”．
刘老师：“A型客车每辆每天的租金比B型客车高150元．八年级师生上周在这个客运公司租了4辆A型客车和2辆B型客车到这两个地方，一天的租金共计5100元．”
根据以上对话，解答下列问题：
（1）每辆A型客车和B型客车可坐师生的人数分别是多少？
（2）该客运公司A型客车和B型客车每辆每天的租金分别是多少元？
（3）若同时租用两种客车，要使每位师生都有座位，且每辆客车恰好坐满
【解答】解：（1）设每辆A型客车可坐师生x人，则每辆B型客车可坐师生（x﹣15）人，
根据题意得：＝，
解得：x＝60，
经检验，x＝60是所列方程的解，
∴x﹣15＝60﹣15＝45．
答：每辆A型客车可坐师生60人，每辆B型客车可坐师生45人；
（2）设该客运公司A型客车每辆每天的租金为a元，B型客车每辆每天的租金为b元，
根据题意得：，
解得：．
答：该客运公司A型客车每辆每天的租金为900元，B型客车每辆每天的租金为750元；
（3）设租用m辆A型客车，n辆B型客车，
根据题意得：60m+45n＝10+410，
∴m＝6﹣n．
又∵m，n均为正整数，
∴或，
∴该校有2种租车方案，
方案1：租用5辆A型客车，4辆B型客车；
方案2：租用6辆A型客车，8辆B型客车．
∵6600＜6900，
∴最省钱的租车方案为：租用4辆A型客车，3辆B型客车．
22．（10分）如图，抛物线y＝ax2+bx（a≠0）过点A（4，0），点B是抛物线上一个动点，使边CD在x轴上（点C在点D的左侧），点E在抛物线上，当时，．
（1）求抛物线的解析式；
（2）当m为何值时，四边形BCDE是正方形？
【解答】解：（1）∵抛物线y＝ax2+bx（a≠0）过点A（5，0），
∴16a+4b＝7，
∴b＝﹣4a，
∴抛物线的解析式为y＝ax2﹣4ax，
当m＝时，BC＝，
即B（，），
把点B坐标代入y＝ax2﹣4ax得，
＝a﹣6a×，
解得a＝﹣3，
∴抛物线解析式为y＝﹣x2+4x；
（2）当四边形BCDE是正方形时，BC＝CD，
∵OA＝7，OC＝m，
∴CD＝4﹣2m，
∴B（m，7﹣2m），
把点B坐标代入y＝﹣x2+4x得，﹣m2+4m＝2﹣2m，
整理得：m2﹣8m+4＝0，
解得m＝6﹣或m＝3+，
∴当m＝3﹣时，四边形BCDE是正方形．
23．（10分）综合与实践：
综合与实践课上，老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动．
（1）操作判断：
如图1，先用对折的方式确定矩形ABCD的边AB的中点E，再沿DE折叠，把纸片展平，延长DF
请写出线段FG与线段BG的数量关系 FG＝BG ；
（2）迁移思考：
如图2，把▱ABCD按照（1）中的操作进行折叠和作图，BG这两条线段之间的数量关系，并仅就图2证明你的判断．
（3）拓展探索：
如图1，若AB＝2，按照（1），请直接写出当CG＝1时AD的值．
【解答】解：（1）连接EG，
∵四边形ABCD是矩形，
∴∠A＝∠B＝90°，
∵点E是AB的中点，
∴AE＝BE，
由折叠知，AE＝EF，
∴EF＝EB，
在Rt△EFG和Rt△EBG中，
，
∴Rt△EFG≌Rt△EBG（HL），
∴FG＝BG，
故答案为：FG＝BG；
（2）FG＝BG，证明如下：
连接FB，
∵四边形ABCD是平行四边形，
∴∠A+∠B＝180°，
∵点E是AB的中点，
∴AE＝BE，
由折叠知，AE＝EF，∠DFE+∠EFG＝180°，
∴EF＝EB，∠EBG＝∠EFG，
∴∠EFB＝∠EBF，
∵∠EFB+∠BFG＝∠EBF+∠FBG，
∴∠BFG＝∠FBG，
∴FG＝BG；
（3）∵四边形ABCD是矩形，AB＝2，
∴CD＝AB＝2，
∴DG＝＝＝，
令AD＝x，则DF＝AD＝x，
由（1）知FG＝BG＝x﹣1，
∴x+x﹣1＝，
解得x＝，
即AD的长为．鞋号
35
36
37
38
39
40
41
42
43
销售量/双
2
4
5
5
12
6
3
2
1
项目
统计量
AI软件
信息处理速度得分
信息识别准确度得分
平均数
中位数
众数
平均数
方差
甲
7.3
7
b
5.6
S甲2
乙
7.65
a
7
4.9
S乙2
鞋号
35
36
37
38
39
40
41
42
43
销售量/双
2
4
5
5
12
6
3
2
1
项目
统计量
AI软件
信息处理速度得分
信息识别准确度得分
平均数
中位数
众数
平均数
方差
甲
7.3
7
b
5.6
S甲2
乙
7.65
a
7
4.9
S乙2