广东省江门市第一中学2023-2024学年高一启超学院创新班下学期3月月考数学试题（原卷版+解析版）

这是一份广东省江门市第一中学2023-2024学年高一启超学院创新班下学期3月月考数学试题（原卷版+解析版），文件包含广东省江门市第一中学2023-2024学年高一启超学院创新班下学期3月月考数学试题原卷版docx、广东省江门市第一中学2023-2024学年高一启超学院创新班下学期3月月考数学试题解析版docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
一、单项选择题（本题共8小题，每题5分，共40分）
1. 已知集合，则（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】先化简集合，再根据交集的定义即可求解.
【详解】因为，
所以.
故选：B
2. 命题“”的否定为（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】根据存在命题的否定为全称命题分析即可.
【详解】命题“”的否定为“”.
故选：B
3. 设、、为实数，且，则下列不等式正确的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据不等式的性质判断A、D，利用特例说明B，利用作差法判断C.
【详解】因为、、为实数，且，
所以，，，，故A错误，D正确；
当时，故B错误，
因为，所以，故C错误；
故选：D
4. 如图所示，两个大圆和一个小圆分别表示集合、、，它们是的三个子集，则阴影部分所表示的集合是（ ）

A. B.
C. D.
【答案】C
【解析】
【分析】题图中的阴影部分是的子集，但该子集中不含集合中的元素，且该子集包含于集合的补集，用关系式表示出来即可．
【详解】由图知，首先阴影部分是的子集，其次不含集合中的元素且在集合的补集中，
可得阴影部分所表示的集合是或.
故选：C.
5. 的最小值等于（ ）
A. 3B. C. 2D. 无最小值
【答案】A
【解析】
【分析】利用基本不等式计算可得.
【详解】因为，则，所以，
当且仅当，即，时取等号，
所以的最小值等于.
故选：A
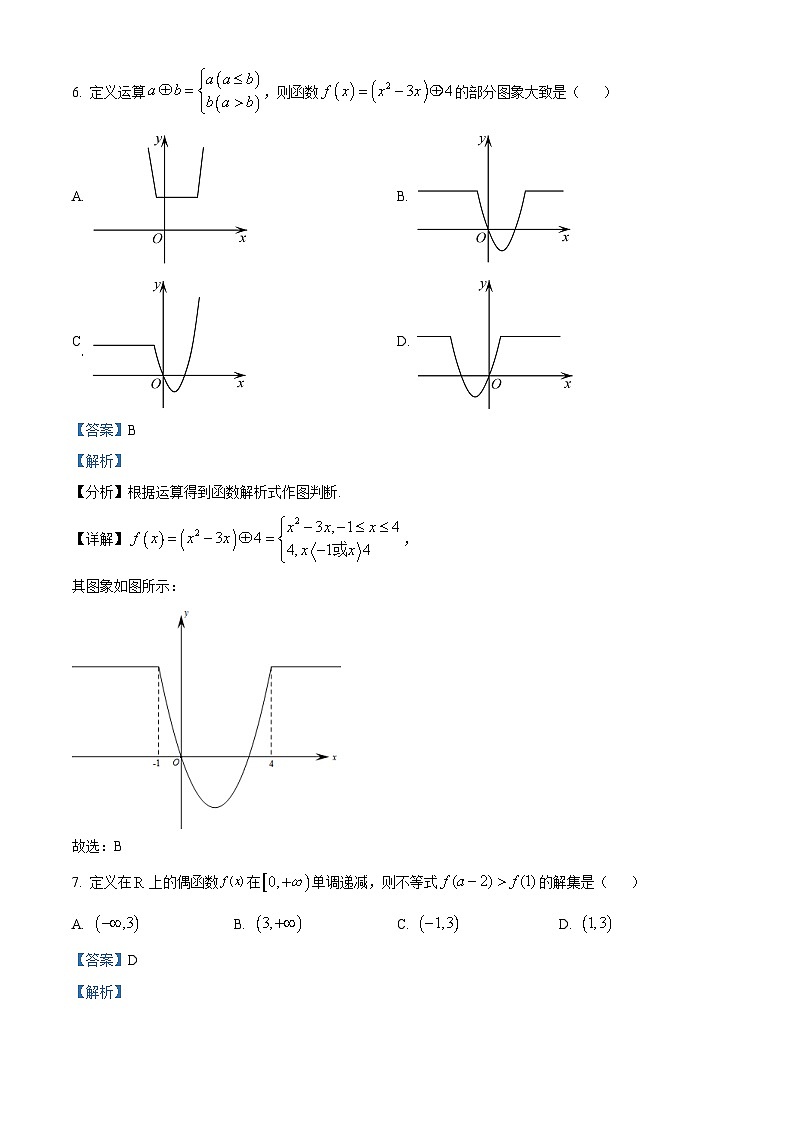
6. 定义运算，则函数的部分图象大致是（ ）
A. B.
C D.
【答案】B
【解析】
【分析】根据运算得到函数解析式作图判断.
【详解】，
其图象如图所示：
故选：B
7. 定义在上的偶函数在单调递减，则不等式的解集是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据偶函数的单调性将函数不等式转化为自变量的不等式，解得即可.
【详解】因为定义在上的偶函数在单调递减，
不等式等价于，等价于，
即，解得，即不等式的解集是.
故选：D
8. 高斯是德国著名的数学家，近代数学奠基者之一，用他的名字命名了“高斯函数”.设，用表示不超过x的最大整数，则标为高斯函数.例如：，已知函数，则下列选项中，正确的是（ ）
A.
B. 的最大值为1
C. 的最小值为0
D. 在上的值域为
【答案】C
【解析】
【分析】先进行分段化简函数，并画函数图象，再结合图象判断最值情况即可.
【详解】对于A，，，所以，A错；
由高斯函数的定义可得：
当时，，则，
当时，，则，
当时，，则，
当时，，则，
当时，，则，
当时，，则，
当时，，则，
所以当时，，且每段函数都是单调递减，每段的左端点的函数值都为1；
当时，，且每段函数都是单调递增，每段的左端点的函数值都为1；
绘制函数图象如图所示，

对于B，由图可知，当，没有最大值，B错；
对于C，由图可知，当，的最小值为0，C对；
对于D，由图可知，在上的值域为，D错.
故选：C
二、多项选择题（本题共3小题，每题6分，共18分）
9. 德国著名数学家狄利克雷在数学领域成就显著，是解析数论的创始人之一，以其命名的函数，称为狄利克雷函数，则关于，下列说法正确的是（ ）
A. 的值域为B. 的定义域为
C. ，D. 为偶函数
【答案】BCD
【解析】
【分析】根据函数解析式结合函数的定义域、值域和奇偶性逐一判断即可．
【详解】因为函数，所以函数的定义域为，值域为，故A错误，B正确；
因为或且0与1均为有理数，所以或，故C正确；
函数，故为偶函数，D正确．
故选：BCD
10. 已知关于的不等式的解集为或，则（ ）
A.
B.
C. 不等式的解集是
D. 不等式与的解集相同
【答案】AB
【解析】
【分析】依题意和为方程的两根，利用韦达定理得到方程组，即可求出、的值，再解一元二次不等式和分式不等式即可.
【详解】因为关于的不等式的解集为或，
所以和为方程的两根，所以，解得，故A正确，B正确；
不等式即，所以，即，
解得或，所以不等式解集为，故C错误；
不等式等价于，解得或，故不等式的解集为或，所以D错误；
故选：AB
11. 设函数，集合，设，则下列说法正确的是（ ）.
A. B. 一定等于9
C. 可能等于8D. 时，
【答案】ABD
【解析】
【分析】由解集为正整数解集可知，，，再结合，即可判断各选项.
【详解】令，则，
因为解集为正整数解集，而，
当时，；当时，；
当时，，符合正整数解集.
因只有3个正整数解，又，所以
对于A，，A对；
对于B， ，B对；
对于C，由B选项可知，C错；
对于D，时，，D对.
故选：ABD.
三、填空题（本题共3小题，每题5分，共15分）
12. 设，则“”是“ ”的_____条件.（选填“充分必要”、“充分不必要”、“必要不充分”、“既不充分也不必要”）
【答案】必要不充分
【解析】
【分析】先解不等式，再根据充要条件的定义即可判断.
【详解】解不等式可得，
因为“”能推出“”， “”不能推出“”，
所以“”是“ ”的必要不充分条件.
故答案为：必要不充分.
13. 函数在区间上单调递增，则的取值范围是_____.
【答案】
【解析】
【分析】分，，三种情况讨论，结合二次函数的性质得到不等式组，解得即可.
【详解】因为，
当时函数在定义域上单调递减，不符合题意，
当时，函数开口向下，不可能在上单调递增，不符合题意，
当时函数开口向上，对称轴，要使函数在区间上单调递增，
所以，解得，所以的取值范围是.
故答案为：
14. 设集合，，函数.
（1）______；
（2）若，则t的取值范围是______.
【答案】 ①. ②. .
【解析】
【分析】
（1）根据题意，由函数的解析式分析可得的值，进而计算可得答案；（2）根据题意，按的取值范围分情况讨论，分析的取值范围，求出的解析式，据此分析的解集，即可得答案．
【详解】（1）根据题意，，即，
则，
则；
（2）根据题意，分2种情况讨论：
①、当时，，则有，此时，
若，即，解可得：，
此时的取值范围为，；
②、当时，，则有，
其中当时，，此时，若，即，解可得：，舍去
当时，，此时，若，即，解可得：，
此时的取值为，；
综合可得：的取值范围为，．
【点睛】本题主要考查分段函数的应用，涉及函数值的计算，意在考查学生对这些知识的理解掌握水平，分类讨论是解决本题的关键.
四、解答题（本题共5小题，共77分）
15. 已知函数，，满足条件，.
（1）求的解析式；
（2）用单调性的定义证明在上的单调性，并求在上的最值.
【答案】（1）
（2）单调递减，证明见解析，，
【解析】
【分析】（1）根据，代入得到方程组，解得即可；
（2）利用定义法证明，再根据单调性求出函数的最值.
小问1详解】
因为且，，
所以，解得，所以.
【小问2详解】
在上单调递减，证明如下：
由，
设任意的且，
则
，
因为且，所以，，，
所以，则在上单调递减，
所以，.
16. 设函数，.
（1）若，，求的最小值；
（2）若在上恒成立，求实数的取值范围.
【答案】（1）
（2）
【解析】
【分析】（1）由可得，再利用乘“1”法及基本不等式计算可得；
（2）依题意可得在上恒成立，即可得到，解得即可.
【小问1详解】
因为且，
所以，即，
又，，所以，
当且仅当，即，时取等号，
即的最小值为.
【小问2详解】
因为在上恒成立，
即在上恒成立，又，
所以在上恒成立，
因为，所以，解得，
即实数的取值范围为.
17. 佩戴口罩能起到一定预防新冠肺炎的作用，某科技企业为了满足口罩的需求，决定开发生产口罩的新机器.生产这种机器的月固定成本为万元，每生产台，另需投入成本（万元），当月产量不足70台时，（万元）；当月产量不小于70台时，（万元）.若每台机器售价万元，且该机器能全部卖完.
（1）求月利润（万元）关于月产量（台）的函数关系式；
（2）月产量为多少台时，该企业能获得最大月利润？并求出其利润.
【答案】（1）；（2）当月产量为台时，该企业能获得最大月利润，其利润为万元.
【解析】
【分析】
（1）根据题意分别列出当及时，关于的解析式即可；
（2）根据二次函数的性质计算当时，的最大值，根据基本不等式求解当时的最大值，然后比较得出最值.
【详解】（1）当时，；
当时，
∴
（2）当时，；
当时，取最大值万元；
当时， ，
当且仅当时，取等号
综上所述，当月产量为台时，该企业能获得最大月利润，其利润为万元.
【点睛】本题考查函数的实际应用问题，考查基本不等式的实际应用，难度一般.解答时，根据题目条件列出函数的解析式是关键.
18. 已知函数是定义在R上的奇函数，且当时，.
（1）求函数的解析式并画出其图像；

（2）设函数在上的最大值为，求.
【答案】（1）；图象见解析；
（2）
【解析】
【分析】（1）利用奇函数的定义即可求函数的解析式，并可以画出图象，
（2）对进行分类讨论，由图象即可求出函数的最大值．
【小问1详解】
由是定义在上的奇函数，可得，
当时，，
那么，则，
所以
函数的解析式为，图象如下：
【小问2详解】
由图象可知：
当时，在上单调递增，；
时，令，解得，
当时， ；
当时， .
所以.
19. 已知函数．
（1）时，①求不等式的解集；②若对任意的，，求实数取值范围；
（2）若存在实数，对任意的都有恒成立，求实数的取值范围．
【答案】（1）①，②，
（2）
【解析】
【分析】（1）①分和两种情况求解即可，②先判断函数的单调性，然后分，和三种情况求解，
（2）当时，恒成立，所以当时，恒成立，则，得，由，得，然后分和求出和，使可求得结果.
【小问1详解】
当时，，
①由，得，
当时，，解得，
当时，恒成立，得，
综上，
所以不等式的解集为，
②因为，
所以在上为增函数，
当时，不恒成立，
当时，由，得，
所以，所以恒成立，
所以，此时不存在，
当时，由，得，
所以，所以恒成立，
所以，得，
综上，，即实数取值范围为，
【小问2详解】
由，得，
当时，恒成立，
当时，恒成立，所以，
所以，得，
由，得，得，
当时，，，
所以，
所以存在满足以上不等式，则，得，此时，
当时，，，
所以有解，
所以，解得，
综上可得，即实数的取值范围为
【点睛】关键点点睛：此题考查不等式恒成立问题，第（2）问解题的关键是将问题转化为当时，恒成立，则，然后转化为求，考查数学转化思想和计算能力，属于难题.