2024七年级数学下册培优专项1.5平移综合应用必刷试题（附解析浙教版）

这是一份2024七年级数学下册培优专项1.5平移综合应用必刷试题（附解析浙教版），共12页。

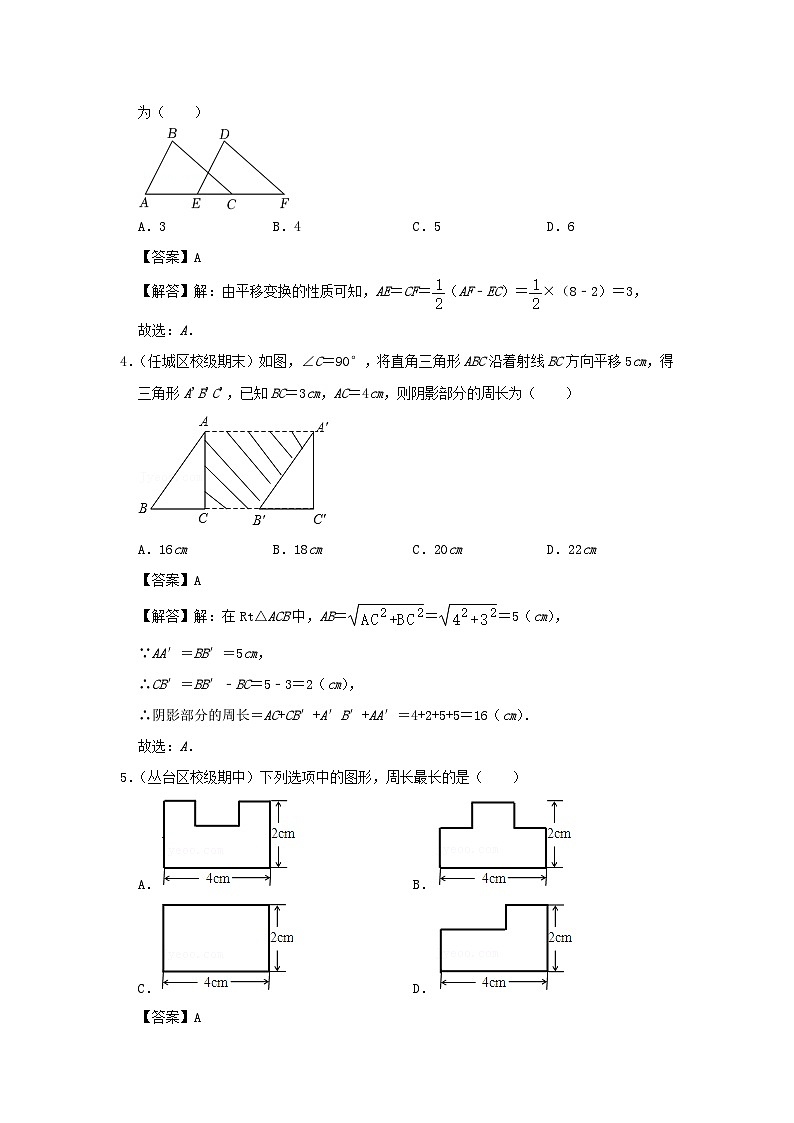
专项1.5 平移综合应用必刷1．（海沧区校级期末）如图，将直角三角形ABC沿AB方向平移得到直角三角形DEF．已知AD＝4，AE＝13，则DB长为（　　）A．4 B．5 C．9 D．13【答案】B【解答】解：∵AB＝DE，∴AD＝BE＝4，∵AE＝13，∴BD＝13﹣4﹣4＝5，故选：B．2．（上蔡县期末）如图，将三角形ABC沿BC方向平移3cm得到三角形DEF，若四边形ABFD的周长为20cm，则三角形ABC的周长是（　　）A．14cm B．17cm C．1lcm D．8cm【答案】A【解答】解：由平移的性质可知，AC＝DF，BC＝EF，AD＝CF＝BE＝3cm，∵四边形ABFD的周长为20cm，即AB+BC+CF+DF+AD＝20cm，∴AB+BC+AC+CF+AD＝20cm，∴AB+BC+AC＝20﹣3﹣3＝14（cm），即三角形ABC的周长是14cm，故选：A．3．（孝南区期末）如图，把△ABC沿AC方向平移得到△FDE，AF＝8，EC＝2，则平移的距离为（　　）A．3 B．4 C．5 D．6【答案】A【解答】解：由平移变换的性质可知，AE＝CF＝（AF﹣EC）＝×（8﹣2）＝3，故选：A．4．（任城区校级期末）如图，∠C＝90°，将直角三角形ABC沿着射线BC方向平移5cm，得三角形A'B'C'，已知BC＝3cm，AC＝4cm，则阴影部分的周长为（　　）A．16cm B．18cm C．20cm D．22cm【答案】A【解答】解：在Rt△ACB中，AB＝＝＝5（cm），∵AA′＝BB′＝5cm，∴CB′＝BB′﹣BC＝5﹣3＝2（cm），∴阴影部分的周长＝AC+CB′+A′B′+AA′＝4+2+5+5＝16（cm）．故选：A．5．（丛台区校级期中）下列选项中的图形，周长最长的是（　　）A． B． C． D．【答案】A【解答】解：选项B，C，D中的周长都是12cm，选项A的周长大于12cm，故选：A．6．（方城县期末）如图所示，将直角三角形ABC（∠C＝90°）沿CB方向平移CF的长度后，得到直角三角形DEF．已知DG＝4，CF＝6，AC＝10，则图中阴影部分的面积是（　　）A．60 B．50 C．40 D．30【答案】A【解答】解：∵将△ABC沿CB向右平移得到△DEF，CF＝6，∴AD∥BE，AD＝BE＝6，∴四边形ABED是平行四边形，∴四边形ABED的面积＝BE×AC＝6×10＝60．故选：A．7．（厦门期末）如图，将三角形ABC平移得到三角形DEF，点A的对应点是点D，则线段BC的对应线段是（　　）A．EF B．DE C．BE D．CF【答案】A【解答】解：由平移的性质可知，BC的对应线段是EF，故选：A．8．（东平县校级期末）如图，将线段AB平移到线段CD的位置，则a+b的值为（　　）A．4 B．0 C．3 D．﹣5【答案】A【解答】解：由题意，线段AB向左平移3个单位，再向上平移4个单位得到线段CD，∴a＝5﹣3＝2，b＝﹣2+4＝2，∴a+b＝4，故选：A．9．（莱州市期末）如图，△ABC的边长AB＝3cm，BC＝4cm，AC＝2cm，将△ABC沿BC方向平移acm（a＜4），得到△DEF，连接AD，则阴影部分的周长为　　cm．【答案】9【解答】解：∵将△ABC沿BC方向平移acm（a＜4cm），得到△DEF，∴AD＝BE，AB＝DE，AC＝DF，∴阴影部分的周长＝AD+EC+DE+AC＝BE+EC+AC+AB＝AB+AC+BC＝3+4+2＝9cm，故答案为：9．10．（芝罘区期末）如图，已知△ABC的面积为12，将△ABC沿BC平移到△A'B'C'，使B'和C重合，连接AC'交A'C于D，则△C'DC的面积为　　【答案】6【解答】解：根据题意得，∠B＝∠A′CC′，BC＝B′C′，∴CD∥AB，CD＝AB（三角形的中位线），∵点C′到A′C的距离等于点C到AB的距离，∴△C′DC的面积＝△ABC的面积＝×12＝6．故答案为：6．11．（左权县期中）如图所示，直角三角形ABO的周长为100，在其内部的n个小直角三角形周长之和为　　．【答案】100【解答】解：由平移的性质可得，n个小直角三角形较长的直角边平移后等于AO边，较短的直角边平移后等于BO边，斜边之和等于AB边长，∴n个小直角三角形的周长之和＝Rt△AOB的周长，∵直角三角形AOB的周长为100，∴这n个小直角三角形的周长之和＝100．故答案为：100．12．（前郭县月考）如图，已知三角形ABC的面积为12，将三角形ABC沿BC平移到三角形A′B′C′，使B′和C重合，连接AC′交A′C于D，D是A′C的中点，则三角形C′DC的面积为　　．【答案】6【解答】解：根据题意得，∠B＝∠A′CC′，BC＝B′C′，∴CD∥AB，CD＝AB（三角形的中位线），∵点C′到A′C的距离等于点C到AB的距离，∴△C′DC的面积＝△ABC的面积＝×12＝6．故答案为：6．（龙湖区期末）如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为　　cm2．【答案】6【解答】解：由题意，阴影部分是矩形，长为5﹣2＝3（cm），宽为3﹣1＝2（cm），∴阴影部分的面积＝2×3＝6（cm2），故答案为6．14．（澧县校级期末）大正方形的边长为4厘米，小正方形的边长为2厘米，起始状态如图所示，现把小正方形以1厘米/秒的速度向右沿直线平移，同时大正方形以1厘米/秒的速度向左沿直线平移，设平移的时间为t秒，两个正方形重叠部分的面积为S平方厘米．当S＝2时，平移的时间为　　秒．【答案】0.5秒或2.5．【解答】解：当S＝2时，重叠部分长方形的宽＝2÷2＝1cm，重叠部分在大正方形的左边时，t＝1÷2＝0.5秒，重叠部分在大正方形的右边时，t＝（4+2﹣1）÷2＝2.5秒，综上所述，小正方形平移的时间为0.5或2.5秒；故答案为：0.5秒或2.5．15．（丛台区校级期中）如图，在△ABC中，AB＝4cm，BC＝3cm，AC＝3cm，将△ABC沿着与AB垂直的方向向上平移2cm，得到△FDE，则阴影部分的面积　　．【答案】8cm2【解答】解：由平移可得，DF＝AB，DF∥AB，∴四边形ABDF是平行四边形，又由平移的方向可得，∠ABD＝90°，∴四边形ABDF是矩形；由平移可得，△ABC≌△FDE，BD＝2cm，∴S△ABC＝S△FDE，∴阴影部分的面积＝矩形ABDF的面积＝AB•BD＝4×2＝8cm2．故答案为：8cm2．16．（大石桥市期末）如图所示，在长为50m，宽为25m的草坪上修了一条恒为1m宽的弯曲小路，则余下草坪的面积为　m2．【答案】1200　【解答】解：∵把宽度为1m的弯曲小路分割成若干个四边形，这些四边形等于一个宽度为1m的矩形，如图矩形ABCD，∴小路为宽恒为1m的弯曲小路，∴面积为50×1＝50（m2），∴余下草坪的面积为50×25﹣50＝1200（m2），故答案为：1200．17．（邗江区期末）如图是某公园里一处矩形风景欣赏区ABCD，长AB＝50米，宽BC＝30米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那么小明沿着小路的中间出口A到出口B所走的路线（图中虚线）长为　　米．【答案】108【解答】解：利用已知可以得出此图形可以分为横向与纵向分析，横向距离等于AB，纵向距离等于（AD﹣1）×2，∴图是某公园里一处矩形风景欣赏区ABCD，长AB＝50米，宽BC＝30米，为50+（30﹣1）×2＝108米，故答案为：108．18．如图，直线l上摆放着直角三角形纸板DCE，∠DCE＝90°，将三角板ECD沿直线l向左平移到图中的三角板E'C'D'位置，P为EC与E'D'的交点．（1）求证：∠CPD'＝∠E；（2）E'C'＝8，C'C＝2，EP＝1.5，求阴影部分的面积．【解答】（1）证明：由平移的性质得CE∥C′E′，CC＝′EE′＝DD′，∴四边形CC′E′E是平行四边形，∴EE′∥CC′，∴DD′∥EE′∴四边形DD′E′E是平行四边形，∴DE∥DD′，∴∠CPD'＝∠E；（2）解：∵将三角板ECD沿直线l向左平移到图中的三角板E'C'D'位置，∴CE＝C′E′＝8，∵EP＝1.5，∴CP＝6.5，∴阴影部分的面积＝S四边形C′E′PC＝（6.5+8）×2＝14.5．19．（海南期末）如图，在Rt△ABC中，∠ACB＝90°，∠E＝55°，将△ABC沿AB方向向右平移得到△DEF．（1）求∠A的度数；（2）若AE＝8cm，DB＝2cm，请求出AD的长度．【解答】解：（1）∵BC∥EF，∴∠ABC＝∠E＝55°，∵∠ACB＝90°，∴∠A＝90°﹣55°＝35°；（2）由平移得，AD＝BE＝CF，∵AE＝8cm，DB＝2cm，∴AD＝BE＝×（8﹣2）＝3（cm）．20．（萨尔图区校级期末）某酒店在重新装修后，准备在大厅的主楼梯上铺设某种红色地毯，已知这种地毯每平方米的售价为40元，主楼梯道宽为3米，其侧面如图所示；铺设梯子的红地毯至少需要多长？花费至少多少元？【解答】解：地毯的长度至少为：2.6+5.8＝8.4米；8.4×3×40＝1008（元）．答：铺设梯子的红地毯至少需要8.4米，花费至少1008元．21．（弥勒市校级月考）如图，把直角梯形ABCD沿AD方向平移到梯形EFGH，HG＝24cm，WG＝8cm，CW＝6cm，求阴影部分面积．【解答】解：由平移的性质，梯形ABCD的面积＝梯形EFGH的面积，CD＝HG＝24cm，∴阴影部分的面积＝梯形DWGH的面积，∵CW＝6cm，∴DW＝CD﹣CW＝24﹣6＝18cm，∴阴影部分的面积＝（DW+HG）•WG＝（18+24）×8＝168cm2．答：阴影部分面积是168cm2．22．（瀍河区月考）如图所示，一块长为18m，宽为12m的草地上有一条宽为2m的曲折的小路，求这块草地的绿地面积．【解答】解：绿地的面积为：（18﹣2）×（12﹣2）＝160（m2），答：这块草地的绿地面积是160m2．23．（抚州期末）如图，已知直线AB∥CD，∠A＝∠C＝100°，点E，F在CD上，且满足∠DBF＝∠ABD，BE平分∠CBF．（1）直线AD与BC有何位置关系？请说明理由；（2）求∠DBE的度数；（3）若平行移动AD，在平行移动AD的过程中是否存在∠BEC＝∠ADB？若存在，求出∠BEC的度数；若不存在，请说明理由．【解答】（1）AD∥BC．证明：∵AB∥CD，∴∠A+∠ADC＝180°，又∵∠A＝∠C∴∠ADC+∠C＝180°，∴AD∥BC；（2）解：∵AB∥CD，∴∠ABC＝180°﹣∠C＝80°，∵∠DBF＝∠ABD，BE平分∠CBF，∴∠DBE＝∠ABF+∠CBF＝∠ABC＝40°；（3）存在．解：设∠ABD＝∠DBF＝∠BDC＝x°．∵AB∥CD，∴∠BEC＝∠ABE＝x°+40°；∵AB∥CD，∴∠ADC＝180°﹣∠A＝80°，∴∠ADB＝80°﹣x°．若∠BEC＝∠ADB，则x°+40°＝80°﹣x°，得x°＝20°．∴∠BEC＝∠ADB＝60°．