（期中典型真题）专题8解决问题-江苏省苏州市2023-2024学年五年级下册数学期中高频易错核心考点（苏教版）

这是一份（期中典型真题）专题8解决问题-江苏省苏州市2023-2024学年五年级下册数学期中高频易错核心考点（苏教版），共33页。
1．把33支铅笔和45本练习本平均分给几名三好学生，结果铅笔少2支，练习本多3本。共有几名三好学生？
2．丹顶鹤是国家一级保护动物，2001年全世界野生丹顶鹤约有2000只，其中我国约有500只．我国野生丹顶鹤的数量约占全世界的几分之几？
3．为庆祝建党100周年，希望小学组织各年级学生开展了“红领巾心向党 百年礼赞感党恩”系列活动，其中，四年级40人和五年级48人去参观了红色纪念馆。如果把两个年级的学生分别分成若干个小组，且每个小组的人数相等，每组最多分多少人？两个年级各分了几个小组？
4．用一张长60厘米，宽45厘米的长方形纸剪成同样大小的等腰直角三角形，如果希望纸正好用完，那么至少能剪出多少个这样的等腰直角三角形？
5．东风林场今年栽柳树4800棵，比栽的杉树多702棵，这个林场今年栽杉树多少棵？如果设这个林场今年栽杉树为x棵，则可列方程为( )。
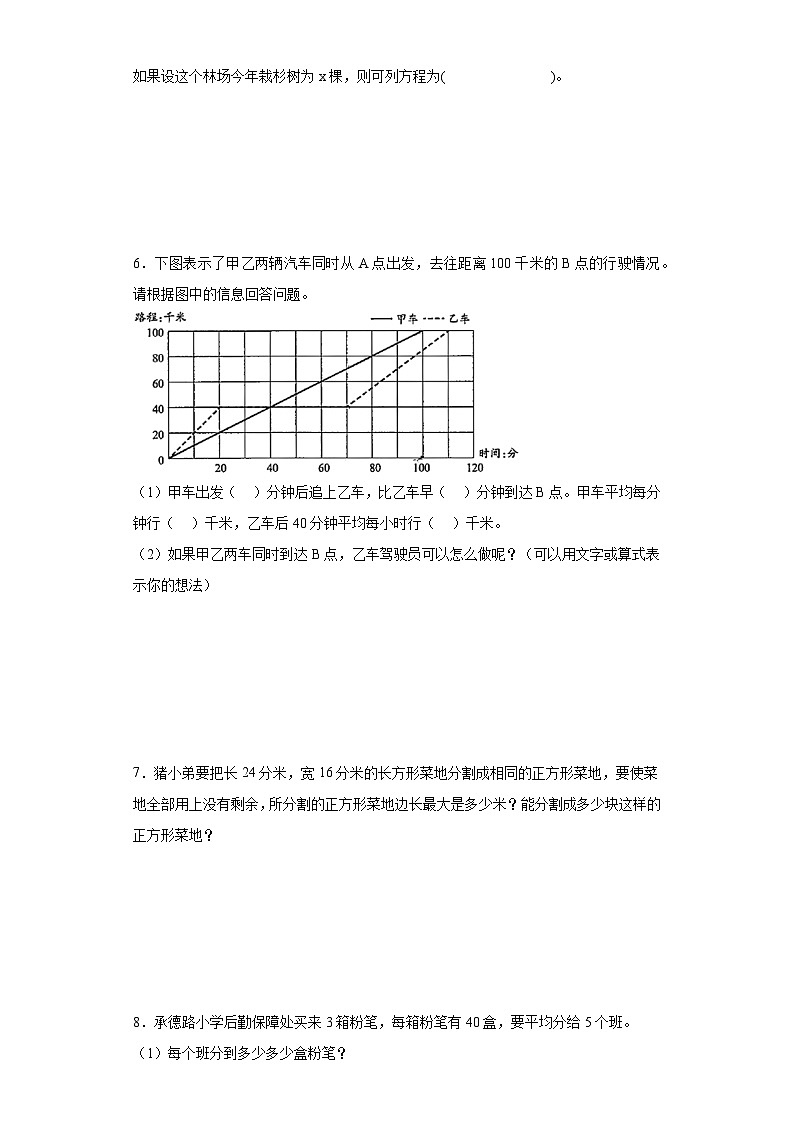
6．下图表示了甲乙两辆汽车同时从A点出发，去往距离100千米的B点的行驶情况。请根据图中的信息回答问题。
（1）甲车出发（ ）分钟后追上乙车，比乙车早（ ）分钟到达B点。甲车平均每分钟行（ ）千米，乙车后40分钟平均每小时行（ ）千米。
（2）如果甲乙两车同时到达B点，乙车驾驶员可以怎么做呢？（可以用文字或算式表示你的想法）
7．猪小弟要把长24分米，宽16分米的长方形菜地分割成相同的正方形菜地，要使菜地全部用上没有剩余，所分割的正方形菜地边长最大是多少米？能分割成多少块这样的正方形菜地？
8．承德路小学后勤保障处买来3箱粉笔，每箱粉笔有40盒，要平均分给5个班。
（1）每个班分到多少多少盒粉笔？
（2）每个班分到几分之几箱粉笔？
（3）每个班可以分得这些粉笔的几分之几？
9．世界人均土地面积大约是2.34公顷，相当于我国人均土地面积的3倍。我国人均土地面积大约是多少公顷？（列方程解答）
10．
（1）买a支铅笔和b个文具盒，共应付多少元？
（2）买c个足球应付多少元？
（3）用100元买了4支铅笔和c个文具盒后，还剩多少元？
11．清明节，实验小学组织五、六年级共420名学生去参加“烈士陵园祭扫”活动。其中六年级参加的人数是五年级1.8倍。五、六年级各参加了多少人？（列方程解答）
12．学校会议室买来4个茶杯和6个果盘，一共花了82.2元。已知每个果盘的单价比每个茶杯贵1.2元，茶杯的单价是多少元？
13．3路每隔6分钟发一次车；5路每隔8分钟发一次车．请问：这两路公共汽车同时发车以后，至少多少分钟两路车才第二次发车？
14．两个年级植树，六年级植树的棵树是五年级的1.6倍，五年级比六年级少植树36棵，两个年级各植树多少棵？
15．一批面包，无论2个装一袋，3个装一袋或是5个装一袋，都正好剩1个。这批面包可能是多少个？最少是多少？
16．李小刚买一个文具盒用去所带钱的一半，买一本笔记本又用去4元，这时还剩16元。李小刚原来带了多少钱？
17．五年级参加植树的有20人,比六年级参加植树的人数的3倍少4人,六年级参加植树的有多少人?
18．一年一度的春季运动会即将开始。据了解，参加径赛运动员的人数是参加田赛运动员人数的1.8倍，田赛运动员人数比径赛少40人。参加田赛、径赛运动员各有多少人？
19．小明买了3本练习本，小芳买了同样的5本。（列方程解答）
20．一个长方形的池塘，长60米，宽42米，如果在它的四周及四角栽柳树，每相邻两棵树之间的距离要相等，那么最少要栽多少棵？如果每两棵柳树之间栽2棵桃树，那么桃树一共栽了多少棵？
21．用2、5、8这三个数字排成一个三位数,使它是2的倍数,共有几种排法?
22．一个书架的上层和下层共有162本书，下层本数是上层的2倍。下层有多少本书？（列方程解答）
23．张大伯有两个儿子都在城里工作，大儿子每6天回一次家，二儿子每9天回一次家。兄弟俩在8月31日同时回家，下一次两人同时回家是几月几日？
24．
五（2）班接种了疫苗加强针的人数占全班的几分之几？和五年级的总体情况相比怎么样？
25．一个小长方形长12厘米、宽10厘米。用这样的小长方形照下面的样子拼成一个正方形，至少需要用多少个这样的小长方形？
26．两地间的路程是210千米，一列客车和一列货车从两地相向开出，3.5小时相遇，客车每小时行驶28千米。货车每小时行驶多少千米？（列方程解决问题）
27．甲乙两车从相距280千米的两地同时出发，相向而行，经过4小时相遇。甲车每小时行驶30千米，乙车每小时行驶多少千米？ （用方程解答）
28．用40个边长1厘米的小正方形拼长方形，一共有几种不同的拼法？周长最长是多少厘米？
29．花花从商店买了4只红色的纸蝴蝶，送给兰兰1只，送给丽丽1只，又从商店买了5只蓝色的纸蝴蝶，又送给丽丽2只，花花送给兰兰的蝴蝶的只数是送给丽丽的蝴蝶数量的几分之几？
30．园林工人在长60米的小路一边每6米栽一棵树（首尾都栽），现在要改为每4米栽一棵树，不用移栽的树有多少棵？
31．学校买来9张课桌和15把椅子，已知9张课桌比15把椅子多付了180元，每把椅子24元，每张课桌多少元？（用方程解）
32．幼儿园买来5箱饼干，每箱18千克，平均分给6个班。
（1）每个班分到多少千克？
（2）每个班分到几分之几箱？
33．王叔叔从海安坐动车去南京，在海安站有26人下车，又有35人上车，这时车上共有365人。原来动车上有多少人？
34．花金鱼的条数是黑金鱼的1.5倍，黑金鱼比花金鱼少50条，花金鱼和黑金鱼各是多少条？（列方程解决）
35．某校准备把45套图书和37个益智玩具分别平均分给数学竞赛一等奖获得者，结果图书剩3套，益智玩具剩2个，那么最多有多少位同学获得一等奖？
36．两根彩带，分别长36分米和48分米，截成同样长的小段，而且没有剩余，每小段最长是多少分米？一共可以截成几小段？
37．甲乙两数的积是90168，已知乙数比甲数少187，问甲数是多少，乙数是多少？
38．萌萌从文具店买了一些同样大小的长方形彩色卡片，长都是8厘米，宽都是6厘米，她想用这些卡片拼成一个正方形，正方形的边长至少是多少厘米？她至少得用多少张这样的长方形卡片就能拼成一个正方形？
39．学校买来24个排球，比篮球多8个。每个篮球72元，是每个排球价钱的1.5倍。（请提出两个不同的问题并解答）
（1） ？
（2） ？
40．某自然保护区内有64只白鹤，比丹顶鹤只数的2.5倍少6只。丹顶鹤有多少只？（列方程解答）
41．小红读一本书，计划12天读完，实际每天比计划多读5页，结果8天读完，这本书共有多少页？
42．今有10个质数：17、23、31、41、53、67、79、83、101、103，如果将它们分成两组，每组五个数，并且两组的五个数之和相等，那么把含有101的这组数从小到大排列，第二个数应是什么？
43．（1）用2、3、5、6四张数字卡片，能摆出多少个不同的两位数？请写出来？
（2）在组成的两位数中，质数和合数各有哪些？奇数和偶数呢？
（3）组成的两位数中，哪些既有因数2，又有因数3？
44．一个筑路队要筑1680米长的路。已经筑了15天，平均每天筑60米。其余的12天筑完，剩下的平均每天筑多少米？
45．用收割机收割面积相同的两块麦田。第一台收割机用1.4小时全部完成，第二台收割机用小时全部完成。哪一台收割机收割得快一些？
46．有两根圆木，一根长20米，另一根长24米。要把它们截成同样长的小段，而且没有剩余，每小段圆木最长是多少米？一共可以截成多少段？
47．一辆汽车运一堆煤，计划每次运4.5吨，20次运完。实际每次运5吨，需要运多少次？
48．现有105个橘子和70个苹果，如果把这些水果装在塑料袋中，要求每个塑料袋中两种水果都有，并且同一种水果在每个塑料袋中的个数相同，那么最多要准备多少个塑料袋？每个塑料袋中有多少个橘子和多少个苹果？
49．同学们为庆祝“六一”儿童节准备了72个苹果，如果每5个摆一盘能正好摆完吗？每盘摆的要一样多，怎样摆才能正好摆完？有几种摆法？
50．下面是万家乐超市甲、乙两个分店去年四个季度的销售额统计图，请你看图回答问题。
（1）甲店（ ）季度销售额最高，乙店（ ）季度销售额最低。
（2）甲乙两店第四季度销售额相差（ ）万元。
（3）甲、乙两个分店平均每个季度的销售额各是多少万元？
参考答案：
1．7名
【分析】33＋2＝35（支），45－3＝42（本）。35支铅笔和42本练习本正好能平均分给这些三好学生，那么三好学生的人数就是35和42的公因数，分别找出它们各自的因数，再从中找出符合题意的公因数即可。
【详解】33＋2＝35（支）
45－3＝42（本）
35的因数有：1、5、7、35。
42的因数有：1、2、3、6、7、14、21、42。
35和42的公因数有1和7。符合题意的是7。
答：共有7名三好学生。
本题考查公因数的实际应用。理解“三好学生的人数就是35和42的公因数”是解题的关键。
2．
【详解】500÷2000=
答：我国野生丹顶鹤的数量约占全世界的．
3．8人；四年级5个；五年级6个
【分析】如果把两个年级的学生分别分成若干个小组，且每个小组的人数相等，则每组的人数既是40的倍数，也是48的倍数，每组最多分多少人，其实是求40和48的最大公因数；
再用各个年级的人数除以每组人数求得分得的组数。
【详解】40＝2×2×2×5
48＝2×2×2×2×3，
所以40和48的最大公因数是2×2×2＝8；
40÷8＝5（组）
48÷8＝6（组）
答：每组最多分8人，四年级分了5个小组，五年级分了6个小组。
此题考查的是最大公因数的应用。解答此题的关键是理解每个小组最多分得的人数是两个年级人数的最大公因数。
4．24个
【解析】同样大小的两个等腰直角三角形可以拼成一个正方形，所以求出这个长方形能够至少能剪出多少个大小相同的正方形，乘2即可求出对应的等腰直角三角形的个数。
【详解】将长60厘米，宽45厘米的长方形纸剪成同样大小的正方形，那么正方形的边长是长和宽的公因数；
60和45的最大公因数是15；
（个）
（个）
（个）
（个）
答：至少能剪出24个这样的等腰直角三角形。
本题考查的是最大公因数的问题，解题的关键在于转化。
5．这个林场今年栽杉树4098棵；x＋702＝4800
【分析】根据题意，今年栽的柳树比栽的杉树多702棵，就可以得出等量关系式：栽杉树的棵树＝栽柳树的棵数－702（据此可解答第一问）；栽杉树的棵数＋702＝栽柳树的棵树（据此可解答第二问）。
【详解】4800－702＝4098（棵）
答：这个林场今年栽杉树4098棵。
列方程为：x＋702＝4800
此题重点考查对“柳树比杉树多702棵”这一重要信息的理解。
6．（1）40；10；1；1.5；
（2）乙车驾驶员可以少休息10分钟
【分析】（1）由图可知，甲车和乙车的路程在出发40分钟后有相交点，说明甲车出发40分钟后追上乙车；甲车出发100分钟后到达B点，乙车出发110分钟后到达B点，所以甲车比乙车提前（110－100）分钟到达B点；根据速度＝路程÷时间，甲车的速度为：100÷100＝1（千米／分）。最后40分钟，乙车走了（100－40）千米，则用（100－40）÷40即可求出乙车后40分钟的速度。
（2）乙车在出发20到70分钟的这段时间，路程不变，说明乙车在行程途中休息了（70－20）分钟，若少休息10分钟，则可以提前10分钟到达，也就是100分钟可以到达（答案不唯一）。
【详解】（1）110－100＝10（分钟）
100÷100＝1（千米／分）
（100－40）÷40
＝60÷40
＝1.5（千米／分）
即甲车出发40分钟后追上乙车，比乙车早110－100＝10分钟到达B点。甲车平均每分钟行1千米，乙车后40分钟平均每小时行1.5千米。
（2）乙车在行程途中休息了（70－20）分钟，若少休息10分钟，则可以提前10分钟到达，此时甲乙两车同时到达B点。
本题主要考出复式折线统计图，读懂题干信息是解题的关键。
7．8米；6块
【分析】将一个长方形分割成大小相等的正方形，且没有剩余，就是求长方形的长和宽的最大公因数；最大公因数就是可以分割成的正方形的边长，然后再根据面积就可以算出可以分成了几块了。
【详解】24＝2×2×2×3；
16＝2×2×2×2；
24和16的最大公因数是2×2×2＝8；
答：所分割的正方形菜地边长最大是8米。
24×16÷（8×8）
＝384÷64
＝6（块）
答：能分割成6块这样的正方形菜地。
此题是典型的求两个数的最大公因数的应用。求两个数的最大公因数，可以将两个数分别分解质因数，然后将它们公有的因数相乘就是最大公因数。
8．（1）24盒；（2）箱；（3）
【分析】（1）每箱粉笔盒数乘箱数求出总共盒数，再除以班级的数量即为每个班分到多少多少盒粉笔；
（2）用粉笔的总箱数除以平均分给的班级的数量，求出每个班分到几分之几箱。
（3）把这些粉笔看作单位“1”，用1除以平均分给的班级的数量，求出每班分到这些粉笔的几分之几。
【详解】（1）40×3÷5
＝120÷5
＝24（盒）
答：每个班分到24盒粉笔。
（2）3÷5＝（箱）
答：每个班分到箱粉笔。
（3）1÷5＝
答：每个班分得这些粉笔的。
解答此题的关键分明确分数与除法的关系，学生应掌握。
9．0.78公顷
【分析】由题意知：我国人均土地面积的3倍等于2.34公顷。据此解答。
【详解】解：设我国人均土地面积大约是公顷。
答：我国人均土地面积大约是0.78公顷。
理解我国人均土地面积的3倍等于2.34公顷这个等量关系是解答本题的关键。
10．（1）（0.5a+20.5b）元；（2）26.8c元；（3）（98﹣20.5c）元
【分析】单价×数量＝总价
【详解】（1）0.5a+20.5b（元）
答：买a支铅笔和b个文具盒，共应付（0.5a+20.5b）元。
（3）100﹣（0.5×4+20.5c）
＝100﹣2﹣20.5c
＝98﹣20.5c（元）
答：还剩（98﹣20.5c）元。
11．五年级150人；六年级270人
【分析】根据关系句中的1份数设x，即设五年级参加了x人，六年级参加1.8x人。并找到等量关系式五年级人数＋六年级人数＝420，列方程解答。
【详解】解：设五年级参加了x人，则六年级参加1.8x人。
x＋1.8x＝420
x＝150
150×1.8＝270（人）
答：五年级参加了150人，六年级参加270人。
分析条件找到1份数设x，并找到等量关系式是解题的关键。
12．7.5元
【分析】设茶杯的单价是x元，那么每个果盘的单价是（1.2＋x）元。等量关系为：4个茶杯的价钱＋6个果盘的价钱＝82.2元，据此列方程解答。
【详解】解：设茶杯的单价是x元，
4x＋（1.2＋x）×6＝82.2
4x＋7.2＋6x＝82.2
10x＋7.2＝82.2
10x＝75
x＝7.5
答：茶杯的单价是7.5元。
解题的关键是根据题意找到等量关系，考查了列方程解应用题。
13．24分钟
【分析】3路车每6分钟发车一次，那么3路车的发车间隔时间就是6的倍数；
5路车每8分钟发车一次，那么5路车的发车间隔时间就是8的倍数；
两辆车同时发车的间隔是6和8的公倍数，最少的间隔时间就是6和8最小公倍数．
【详解】6=2×3
8=2×2×2
6和8的最小公倍数就是：2×2×2×3=24；
两辆车每两次同时发车的间隔是24分钟；
答：至少过24分钟两路车才第二次同时发车．
14．五年级60棵；六年级96棵；
【详解】解：设五年级植树x棵．
1.6x-x=36
x=60
六年级：60×1.6=96（棵）
15．这批面包可能是31个，61个，91个……最少是31个。
【分析】因为剩一个，假设去除一个面包，现在的面包数既是2、3的倍数，又是5的倍数。然后找出符合条件的数字，再加上1，就是面包的数量了。
【详解】2×3×5=30（个）
30×2=60（个）
30×3=90（个）
……
30+1=31（个）
60+1=61（个）
90+1=91（个）
……
答：这批面包可能是31个，61个，91个……最少是31个。
本题中面包无论2个装一袋，3个装一袋或是5个装一袋，都正好剩1个，可以先把剩下的1个面包先排除，最后加上。如果变式2个装一袋，3个装一袋或是5个装一袋，都正好少1个，可以先多一个面包，最后再减去。
16．40元
【分析】设李小刚原来带了x元，根据题意，买一个文具盒用去所带钱的一半，用x÷2，求出一半钱是多少，买一个笔记本又用去4元，等量关系：用带去的钱－买文具盒的钱－买笔记本的钱＝剩下的钱；列方程：x－x÷2－4＝16，解方程，即可解答。
【详解】解：设李小刚原来带了x元
x－x÷2－4＝16
x－0.5x＝16＋4
0.5x＝20
x＝20÷0.5
x＝40
答：李小刚原来带了40元。
解答本题的关键是买一个文具盒用去所带钱的一半，就是把所带钱÷2；进而根据题意，找出等量关系，列方程，解方程。
17．8人
【详解】解:设六年级参加植树的有x人．
3x-4=20
3x=24
x=8
答:六年级参加植树的有8人．
18．田赛：50人；径赛90人
【分析】根据题意，设参加田赛运动员有x人，参加径赛运动员的人数是参加田赛运动员人数的1.8倍，则参加径赛的人数是1.8x人；田赛运动员人数比径赛少40人；它们之间的等量关系为：径赛人数－田赛人数＝40；列方程：1.8x－x＝40，解方程，即可解答。
【详解】解：设参加田赛的运动员有x人，则参加径赛运动员有1.8x人。
1.8x－x＝40
0.8x＝40
x＝40÷0.8
x＝50
径赛人数：50×1.8＝90（人）
答：参加田赛运动员有50人，参加径赛运动员有80人。
本题考查方程的应用，根据题意，找出参加田赛运动员人数与参加径赛运动员人数之间的关系，设出未知数，列方程，解方程。
19．2.5元
【分析】设每本练习本元，等量关系式：小芳应付的钱－小明应付的钱＝5元，据此列方程解答。
【详解】解：设每本练习本元。
答：每本练习本2.5元。
考查了列方程解应用题，关键是弄清题意，找到等量关系式。
20．34棵；68棵
【分析】（1）要求最少要栽多少棵，即每相邻两棵树之间的距离最大，即相邻两棵树之间的距离是60和42的最大公因数，求出60和42的最大公因数，即相邻两棵树之间的距离，即可求出应栽树的棵数；
（2）因为此长方形的池塘四周及四角栽柳树，可以看成是一个封闭的图形，所栽的柳树的棵数和间距数相等，用间距乘2即可解答出所种的桃树的棵数。
【详解】60＝2×2×3×5
42＝2×3×7
60、42的最大公因数是2×3＝6
（60＋42）×2÷6
＝102×2÷6
＝204÷6
＝34（棵）
34×2＝68（棵）
答：最少要种14棵柳树，桃树一共栽了68棵。
关键是理解题意，明白是从求公因数作为突破口，进而找出解决问题的方法。
21．4种
【详解】略
22．108本
【分析】设上层有x本书，则下层有2x本，根据等量关系：上层的本数＋下层的本数＝162本，列方程解答即可。
【详解】解：设上层有x本书，则下层有2x本。
x＋2x＝162
3x＝162
x＝54
54×2＝108（本）
答：下层有108本书。
本题主要考查了列方程解应用题，关键是根据等量关系“上层的本数＋下层的本数＝162本”列方程。
23．9月18日
【分析】根据大儿子每6天回家一次，二儿子每9天回家一次，求出6、9的最小公倍数，即可求出再过多少天他们才能再同时回家，然后进一步解答即可。
【详解】6＝2×3
9＝3×3
6和9的最小公倍数是2×3×3＝18；即再过18天再回家一次。
8月31日＋18天＝9月18日
答：下一次同时回家是9月18日。
本题考查最小公倍数问题：正确理解题意且求出两个数的最小公倍数是关键。
24．；五（2）班疫苗加强针接种情况比整个年级好
【分析】用五（2）班疫苗加强针的人数÷五（2）班总人数，求出五（2）班疫苗加强针的人数占全班人数的分率；再用五年级疫苗加强针的人数÷五年级总人数，求出五年级加强针占五年级总人数的分率；再和五（2）班加强针占全班的分率进行比较，即可解答。
【详解】20÷45＝
45÷150＝
＝；＝
＞；五（2）班疫苗加强针接种情况比整个年级好。
答：五（2）班接种了疫苗加强针的人数占全班的，五（2）班疫苗加强针接种情况比整个年级好。
利用求一个数占另一个数的几分之几；以及分数比较大小的方法进行解答。
25．30个
【分析】求正方形的边长最小是多少厘米，即求12和10的最小公倍数，用短除法即可求出；然后根据求出的正方形的边长，分别除以长和宽，求出排数和列数，进行相乘即可。
【详解】，12和10的最小公倍数是2×6×5＝60；
小长方形数量：（60÷12）×（60÷10）
＝5×6
＝30（个）
答：至少需要用30个这样的小长方形。
此题主要考查的是学生对最小公倍数的实际应用解题能力，需要多加练习同类型题，熟练掌握即可。
26．32千米
【分析】设货车每小时行驶x千米，根据货车速度×时间＋客车速度×时间＝全程，列出方程解答即可。
【详解】解：设货车每小时行驶x千米。
3.5x＋3.5×28＝210
3.5x＋98－98＝210－98
3.5x÷3.5＝112÷3.5
x＝32
答：货车每小时行驶32千米。
本题考查了列方程解决问题，速度×时间＝路程。
27．40千米
【分析】由题意知：（甲车的速度＋乙车的速度）×4＝280。据此列方程解答。
【详解】解：设乙车每小时行驶x千米。
（30＋x）×4＝280
30＋x＝280÷4
30＋x＝70
x＝40
答：乙车每小时行驶40千米。
本题主发考查学生依据速度、时间以及路程之间数量关系解答问题的能力。
28．4种；82厘米
【分析】根据题意可知，长方形的面积是40平方厘米，已知长方形的面积＝长×宽，长方形的周长＝（长＋宽）×2，先找40的因数确定长和宽，再计算周长。
【详解】拼法如下：
长40厘米，宽1厘米
周长：（40＋1）×2
＝41×2
＝82（厘米）；
长20厘米，宽2厘米
周长：（20＋2）×2
＝22×2
＝44（厘米）；
长10厘米，宽4厘米
周长：（10＋4）×2
＝14×2
＝28（厘米）；
长8厘米，宽5厘米
（8＋5）×2
＝13×2
＝26（厘米）
82＞44＞28＞26
答：一共有4种拼法，周长最长是82厘米。
此题主要考查了找因数，注意按一定的顺序找，防止漏写。
29．三分之一
【分析】用送给兰兰的蝴蝶数量除以送给丽丽的蝴蝶数量就是所求，据此解答。
【详解】花花送给兰兰的蝴蝶只数为1只
花花送给丽丽的蝴蝶只数为：1＋2＝3只
所以，兰兰的是丽丽的。
答：花花送给兰兰的蝴蝶只数是送给丽丽的三分之一。
本题在理解上有一定困难，明确送给兰兰的蝴蝶只数和丽丽的只数分别是多少是解决本题的关键。
30．6棵
【分析】因为4和6的最小公倍数是12，所以在距离是12米的倍数的位置上的树不用移栽，用全长除以间距再加上1即可得出不用移栽的树的棵数。
【详解】因为4和6的最小公倍数是12
60÷12＝ 5（棵）
5＋1＝6（棵）
答：不用移栽的树有6棵。
利用4和6的最小公倍数和基本的数量关系求出一边栽树的棵数是解答此题的关键，注意首尾都栽，所以要加1。
31．60元
【详解】解：设每张课桌x元．
9x-15×24=180
x=60
答：每张课桌60元．
32．（1）15千克；（2）箱
【分析】（1）根据题意，用18×5先求出5箱饼干一共有多少千克，进而用饼干的总千克数除以班数，即可求得每个班分到饼干的千克数；
（2）要求每个班分到几分之几箱，就表示把5箱饼干平均分给6个班，就用苹果的箱数除以所分的班数即可得解。
【详解】（1）18×5÷6
＝90÷6
＝15（千克）
答：每个班分到15千克。
（2）5÷6＝（箱）
答：每个班分到箱。
本题考查整数的除法和分数的意义及运用，在解决第二个问题时，苹果的箱数÷班数＝每个班分到的箱数，与每班分得苹果的几分之几区别开来。
33．356人
【分析】设原来动车上有x人，减去下车人数，再加上上车人数，就是此时车上的总人数，据此列方程求解。
【详解】解：设原来动车上有x人。
x－26＋35＝365
x＝365－35＋26
x＝356
答：原来动车上有356人。
本题考查简易方程的应用，关键是熟练运用等式性质解方程。
34．花金鱼150条，黑金鱼100条。
【分析】根据题意，设黑金鱼有x条，则花金鱼有1.5x条。花金鱼的条数－黑金鱼的条数＝50，据此列方程解答。
【详解】解：设黑金鱼有x条，则花金鱼有1.5x条。
1.5x－x＝50
0.5x＝50
x＝100
花金鱼：100×1.5＝150（条）
答：花金鱼有150条，黑金鱼有100条。
列方程解含两个未知数的问题时，设其中的一个未知数为x，用含有x的式子表示另一个未知数，题目中的等量关系是列出方程的关键。
35．7位
【分析】由题意可知，图书和益智玩具如果分的没有剩余，则图书有45－3＝42（套），益智玩具有37－2＝35（个），要想每人分得的数量相等，最多有多少位同学获得一等奖，就是求42和35的最大公因数。据此解答。
【详解】45－3＝42
37－2＝35
42和35的最大公因数是7
答：最多有7位同学获得一等奖。
此题考查的是最大公因数的应用，求两个数的最大公因数的方法是把两个数共有的因数相乘。
36．12分米；7段
【分析】由题意可知：每小段最长的值等于36和48的最大公因数；求每小段最长时，一共截成多少段，用36与48的和除以它们的最大公因数即可。
【详解】36＝2×2×3×3
48＝2×2×2×2×3
所以36和48的最大公因数是2×2×3＝12，即每小段最长是12分米。
（36＋48）÷12
＝84÷12
＝7（段）
答：每小段最长是12分米，一共可以截成7小段。
本题主要考查最大公因数的实际应用，解题的关键是理解每小段最长的值等于36和48的最大公因数。
37．甲数是408，乙数是221
【详解】90168＝2×2×2×3×13×17×17＝221×408
221＋187＝408
所以甲数是408，乙数是221。
38．24厘米；12张
【分析】因为长方形彩色卡片的长都是8厘米，宽都是6厘米，先求出8和6的最小公倍数，长和宽的最小公倍数就是正方形的边长至少的厘米数；
用最小公倍数分别除以长和宽，求出各需要几张，然后相乘就是需要的张数。
【详解】由分析可得：
8＝2×2×2
6＝2×3
2×2×2×3＝24（厘米）
（24÷8）×（24÷6）
＝3×4
＝12（张）
答：正方形的边长至少是24厘米。她至少得用12张这样的长方形卡片就能拼成一个正方形。
39．（1）买来篮球多少个；16个（答案不唯一）
（2）每个排球多少元；48元（答案不唯一）
【分析】（1）知道排球的个数，知道篮球个数与排球个数的关系，即可提买来篮球多少个？由题意可得：篮球个数加8等于排球个数，据此列出方程解答；
（2）知道篮球价格，也知道篮球价格与排球价格的关系，即可提每个排球多少元？由题意可知：排球价格乘1.5等于篮球价格，据此列出方程解答。
【详解】（1）问题：买来篮球有多少个？
解：设篮球有x个。
x＋8＝24
x＝24－8
x＝16
答：买来篮球有16个。
（2）问题：每个排球多少元？
解：设每个排球y元。
1.5y＝72
y＝72÷1.5
y＝48
答：每个排球48元。
此题考查的是列方程与解方程的能力，最主要的是根据题目中的等量关系，提出问题。
40．28只
【分析】设丹顶鹤有x只，等量关系式为：丹顶鹤只数×2.5－6＝白鹤只数，据此列方程解答。
【详解】解：设丹顶鹤有x只。
2.5x－6＝64
2.5x＝70
x＝28
答：丹顶鹤有28只。
列方程是解答应用题的一种有效的方法，解题的关键是弄清题意，找出应用题中的等量关系式。
41．120页
【分析】设计划每天读x页，那么实际每天读x＋5（页），等量关系为：实际每天读的页数×实际天数＝计划每天读的页数×计划天数，据此列方程解答求出x，进而求出这本书的页数。
【详解】解：设计划每天读x页。
（x＋5）×8＝12x
8x＋40＝12x
4x＝40
x＝10
10×12＝120（页）
答：这本书共有120页。
列方程是解答应用题的一种有效的方法，解题的关键找出应用题中的等量关系。
42．31
【分析】本题考查的主要内容是质数和合数应用问题，根据质数和合数的定义进行分析解答。
【详解】这10个质数之和是598，分两组后，每组五个数之和是598÷2＝299；
在有79这组数中，其他四个质数之和是299－79＝220，个位数是0，因此这四个质数的个位数可能有三种情况：
①三个1和一个7；
②两个3和两个7；
③三个3和一个1。
31＋41＋101＝173，220－173＝47，可这十个数中没有47，情形①被否定。
17＋67＝84，220－84＝136，个位数为3的有23、53、83、103，只有53＋83＝136，因此从情形②得到一种分组：17、53、67、79、83和23、31、41、101、103。
所以含有101这组数中，从小到大排列第二个数是31。
从情形③来看，23＋53＋83＋103＝262，262－220＝42，我们能否从53，83，103中找出一个数，用比它少42的数来代替呢？
53－42＝11，83－42＝41，103－42＝61。这十个数中没有11和61，只有41。又得到另一种分组：23、41、53、79、103和17、31、67、83、101。由此可见，不论哪一种分组，含101这组数中，从小到大排列后，第二个数都是31。
此题的解答思路要开阔，考虑要周全，分析所包含的各种情况，提高分析解决问题的能力。
43．（1）能摆出12个不同的两位数，分别是 23、32、25、52、26、62、35、53、36、63、56、65。
（2）质数：23、53
合数：32、25、52、26、62、35、36、63、56、65
奇数：23、25、35、53、63、65
偶数：32、52、26、62、36、56
（3）组成的两位数中，既有因数2，又有因数3的数是36。
【分析】（1）分别以2、3、5、6做十位上的数，另3个数做个位上的数，写出来即可。
（2）只有因数1和它本身的数是质数，至少有三个因数的数是合数，根据因数的个数来判断这个数是质数还是合数；能被2整除的数是偶数，反之的是奇数，据此判断即可。
（3）一个数既有因数2，又有因数3说明这个数有因数2×3＝6，依次看这些数哪个能被6整除即可。
【详解】（1）能摆出12个不同的两位数，分别是 23、32、25、52、26、62、35、53、36、63、56、65。（2）质数：23、53
合数：32、25、52、26、62、35、36、63、56、65
奇数：23、25、35、53、63、65
偶数：32、52、26、62、36、56
（3）在这些数中能被6整除的数只有36，所以既有因数2，又有因数3的数是36。
此题考查了因数倍数的综合应用，质数与合数跟这个数的因数的个数有关，而奇数和偶数主要看能否被2整除。
44．65米
【分析】根据题意设剩下的平均每天筑x米，则有已经筑的天数×平均每天筑的米数＋剩下的天数×剩下平均每天筑的米数＝要筑路的全长，据此列方程解答。
【详解】解：设剩下的平均每天筑x米，则
15×60＋12x＝1680
900＋12x＝1680
12x＝780
x＝65
答：剩下的平均每天筑65米。
认真读题，找出其中的等量关系是解题关键，注意工作总量＝工效×时间。
45．第二台收割机
【分析】同样的任务，用时短的速度快。比较1.4小时和小时的大小即可判断。1.4和，一个是小数，一个是分数，可以把小数化成分数进行比较，也可以把分数化成小数进行比较。
【详解】方法一：把1.4化成分数是＝，＝，＝，＞，则1.4＞，所以第二台收割机收割得快一些。
方法二：把化成小数是4÷3＝，1.4＞，所以第二台收割机收割得快一些。
答：第二台收割机收割得快一些。
这道题的关键是能够灵活运用小数与分数的互化比较大小。
46．4米；11段
【分析】根据“截成同样长的小段，而且没有剩余”可知，就是求20和24的公因数；求“每小段圆木最长是多少米”，即求20和24的最大公因数，用圆木的长度分别除以每小段圆木的长度即可求出两根圆木分别截成的段数，再相加即可。
【详解】20＝2×2×5；
24＝2×2×2×3；
20和24的最大公因数是2×2＝4；
20÷4＋24÷4
＝5＋6
＝11（段）；
答：每小段圆木最长是4米，一共可以截成11段。
解答本题的关键是根据题目中的重点信息确定就是求20和24的最大公因数，从而进一步解答。
47．18次
【详解】解：设每次运5吨，需要运x次。
5x＝4.5×20
x＝18
答：每次运5吨，需要运18次。
48．35个；3个，2个
【分析】要求最多准备多少个塑料袋，也就是求105和70的最大公因数，因为两个数的最大公因数是这两个数公有质因数的乘积；进而求出每个塑料袋中有橘子和苹果的个数。
【详解】把105和70分解质因数：
105＝3×5×7
70＝2×5×7
105和70的最大公因数是5×7＝35
每个袋子中橘子有：105÷35＝3（个）
苹果有：70÷35＝2（个）
答：最多要准备35个塑料袋，每个塑料袋中有3个橘子，2个苹果。
此题属于最大公因数问题，根据求两个数的最大公因数的方法解决问题。
49．不能；有12种摆法．
【详解】试题分析：根据5的倍数特征，个位数字是0或5，则72每5个摆一盘不能正好摆完．要求每盘摆的要一样多，把72分解质因数，分成两个数的积，其中一个数是摆几个，另一个数是摆几盘，有几个计算式，就有几×2个摆法．
解：72个个位数字是2，不是0或5，所以每5个摆一盘不能正好摆完；
72=72×1=2×36=3×24=4×18=6×12=8×9
所以每盘摆的要一样多，每盘摆1个，摆72盘摆完；每盘摆72个，摆1盘摆完；每盘摆2个，摆36盘摆完；每盘摆36个，摆2盘摆完；每盘摆3个，摆24盘摆完；每盘摆24个，摆3盘摆完；每盘摆4个，摆18盘摆完；每盘摆18个，摆4盘摆完；每盘摆6个，摆12盘摆完；每盘摆12个，摆6盘摆完；每盘摆8个，摆9盘摆完；每盘摆9个，摆8盘摆完；有12种摆法．
【点评】此题考查了5的倍数特点，以及分解质因数的方法．
50．（1）一；二
（2）150
（3）562.5万元；592.5万元
【分析】（1）观察统计图，数据点位置越高表示销售额越高，数据点位置越低表示销售额越低；
（2）找到第四季度甲乙两店销售额，求差即可；
（3）根据平均数＝总数÷份数，列式解答即可。
【详解】（1）甲店一季度销售额最高，乙店二季度销售额最低。
（2）750－600＝150（万元）
（3）（700＋500＋450＋600）÷4
＝2250÷4
＝562.5（万元）
（620＋430＋570＋750）÷4
＝2370÷4
＝592.5（万元）
答：甲、乙两个分店平均每个季度的销售额各是562.5万元，592.5万元。
折线统计图的特点不仅能看清数量的多少，还能通过折线的上升和下降表示数量的增减变化情况。复式折线统计图表示2个及以上的量的增减变化情况。