高教版（2021·十四五）基础模块 上册4.5 诱导公式优秀练习题习题课件ppt

这是一份高教版（2021·十四五）基础模块 上册4.5 诱导公式优秀练习题习题课件ppt，文件包含45诱导公式课件pptx、45诱导公式教案docx、45诱导公式课内习题答案docx等3份课件配套教学资源，其中PPT共34页， 欢迎下载使用。

4.5 诱导公式
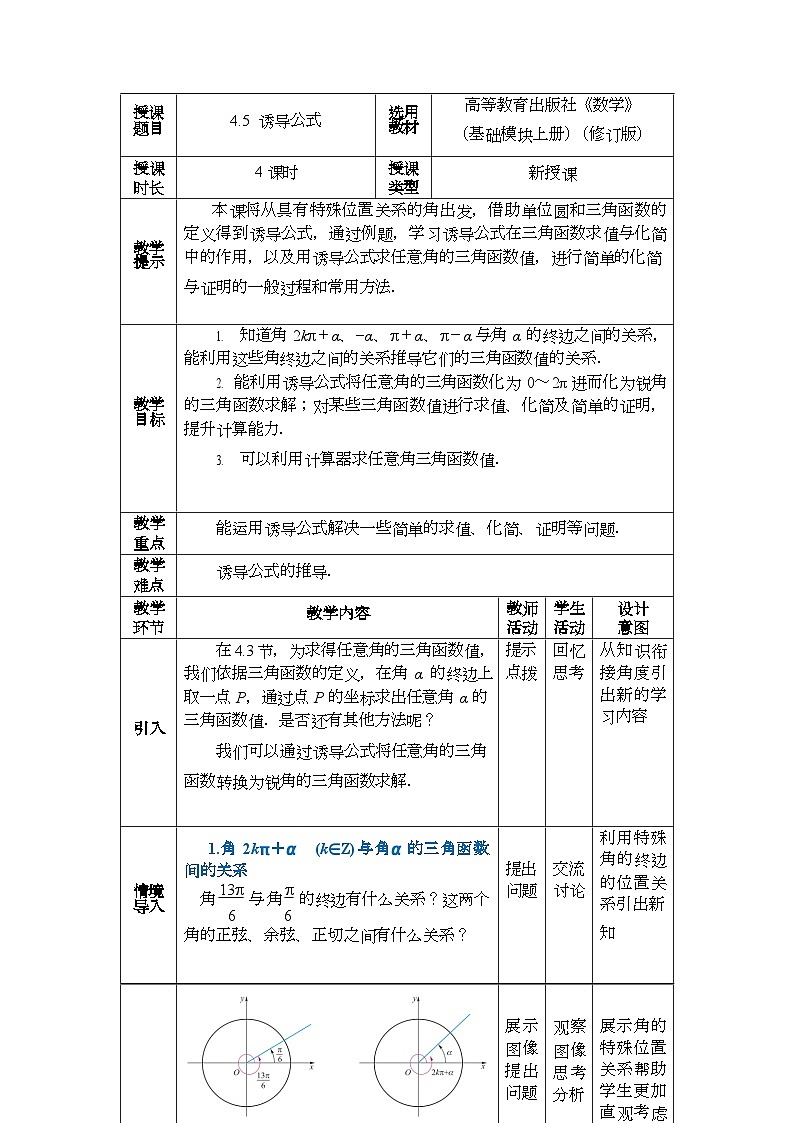
在4.3节，为求得任意角的三角函数值，我们依据三角函数的定义，在角α的终边上取一点P，通过点P的坐标求出任意角α的三角函数值．是否还有其他方法呢？ 我们可以通过诱导公式将任意角的三角函数转换为锐角的三角函数求解．
1.角2k＋ (kZ)与角 的三角函数间的关系
由三角函数的定义可知，终边相同的角的同名三角函数值相等．即
sin(2k＋) = sin；cs(2k＋) = cs；tan(2k＋) = tan ．
利用公式可以将任意角的三角函数转化为[0，2π)内的角的三角函数．
2.角- 与角 的三角函数间的关系
2.角- 与角 的三角函数间的关系-
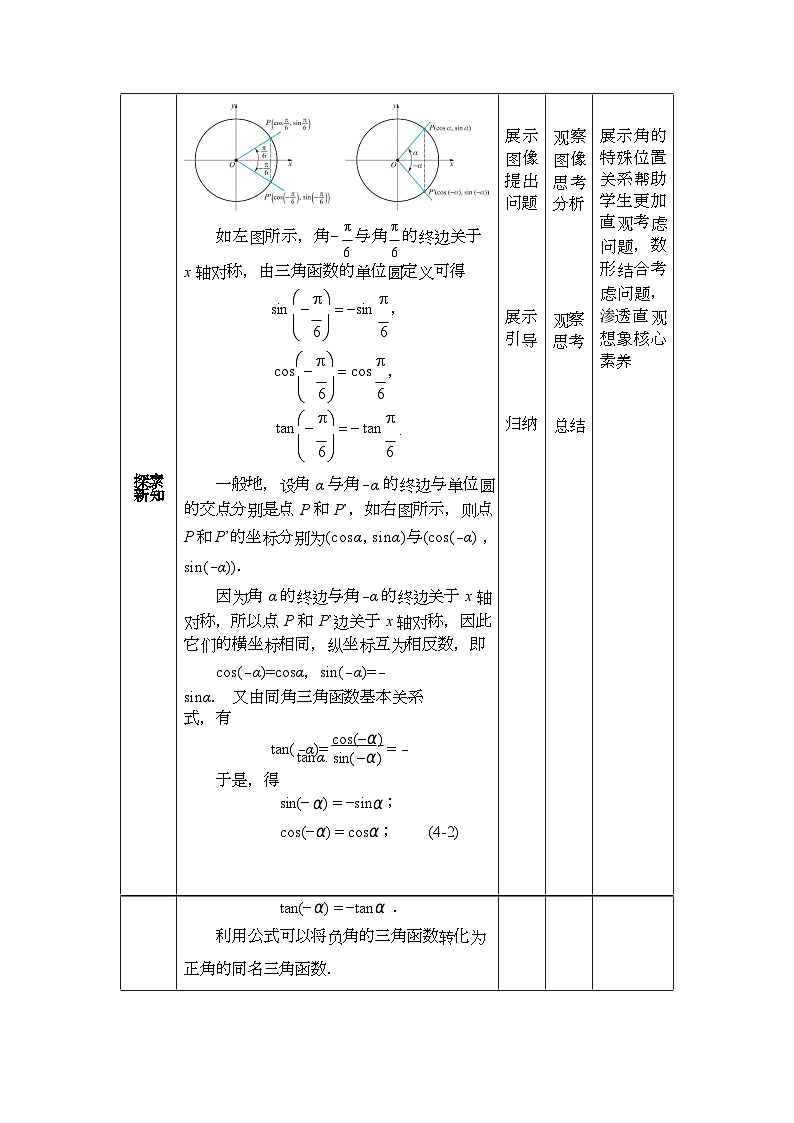
一般地，设角α与角-α的终边与单位圆的交点分别是点P和P’，如图所示，则点P和P’的坐标分别为(csα ， sinα)与(cs(-α) ， sin(-α)) ．
因为角α的终边与角-α的终边关于x轴对称，所以点P和P’边关于x轴对称，因此它们的横坐标相同，纵坐标互为相反数，即cs(-α)=csα，sin(-α)=-sinα．
sin(−) = −sin；cs(−) = cs；tan(−) = −tan ．
利用公式可以将负角的三角函数转化为正角的同名三角函数．
3.角π+ 与角 的三角函数间的关系
一般地，设角α的终边与角π+的终边与单位圆的交点分别是点P和P’，如图所示，则点P和P’的坐标分别为(csα ， sinα)与(cs(π+) ， sin π+)) ．
因为角α的终边与角π+的终边关于原点中心对称，所以点P和P’边关于原点中心对称，因此，它们的横坐标互为相反数相同，纵坐标也互为相反数，即cs(π+)=-csα，sin(π+)=-sinα．
sin(π+) = −sin；cs(π+) = −cs；tan(π+) = tan ．
由公式可将角+α的三角函数转化为角α的同名三角函数．
4.角π- 与角 的三角函数间的关系
一般地，设角α与角π-的终边与单位圆的交点分别是点P和P’，如图所示，则点P和P’的坐标分别为(csα ， sinα)与 (cs(π-) ， sin π-)) ．
因为角α的终边与角π-的终边关于y轴对称，所以点P和P’关于y轴对称，因此，它们的横坐标互为相反数相同，纵坐标相等，即cs(π-)=-csα，sin(π-)=sinα．
sin(π − ) = sin；cs(π − ) = −cs；tan(π − ) = − tan ．
由公式可将角−α的三角函数转化为角α的三角函数．
4.角π - 与角 的三角函数间的关系
sin(π+) =−sin；cs(π+)=−cs；tan(π+) =tan ．
sin(−α) = sinα ；cs(−α)= −csα；tan(−α) = −tanα ．
这些都是三角函数的诱导公式，利用这些公式可以将任意角的三角函数转化为锐角三角函数进行计算．
把任意角的三角函数转化为锐角三角函数的一般步骤是什么？ 可以结合-750°、 225° 、 510° 举例说明．