中考数学（湖南卷）-2024年中考第一次模拟考试

这是一份中考数学（湖南卷）-2024年中考第一次模拟考试，文件包含数学湖南卷全解全析docx、数学湖南卷参考答案及评分标准docx、数学湖南卷考试版A4docx、数学湖南卷答题卡pdf、数学湖南卷考试版A3docx等5份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。

1、锻炼学生的心态。能够帮助同学们树立良好的心态，增加自己的自信心。
2、锻炼学生管理时间。通过模拟考试就会让同学们学会分配时间，学会取舍。
3、熟悉题型和考场。模拟考试是很接近中考的，让同学们提前感受到考场的气氛和布局。
中考的取胜除了平时必要的学习外，还要有一定的答题技巧和良好心态。此外，通过模拟考试还能增强学生们面对高考的信心，希望考生们能够重视模拟考试。
2024年中考第一次模拟考试（湖南卷）
数学·全解全析
第Ⅰ卷
一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
1．有理数的相反数是（ ）
A．B．C．D．
【答案】B
【分析】根据只有符号不同的两个数互为相反数进行解答即可．
【详解】有理数 的相反数是，
故选：．
【点睛】此题考查了相反数的定义，掌握相反数的定义是解题的关键．
2．下列计算中，正确的是（ ）
A．B．
C．D．
【答案】A
【分析】根据积的乘方，完全平方公式，同底数幂的除法，二次根式的加法对各选项进行判断即可．
【详解】解：由题意知，，正确，故A符合要求；
，错误，故B不符合要求；
，错误，故C不符合要求；
，错误，故D不符合要求；
故选：A．
【点睛】本题考查了积的乘方，完全平方公式，同底数幂的除法，二次根式的加法．熟练掌握积的乘方，完全平方公式，同底数幂的除法，二次根式的加法是解题的关键．
3．一元一次方程不等式组的解在数轴上表示正确的是（ ）
A．B．
C．D．
【答案】D
【分析】本题考查的是一元一次不等式组的解法及在数轴上表示解集，在数轴上表示解集时“”，“”要用实心圆点表示；“”，“”要用空心圆点表示．熟练掌握不等式组的解法是解题的关键．先分别解出两个不等式，然后找出解集，表示在数轴上即可．
【详解】解：，
由①得，−，
由②得，，
故原不等式组的解集为：．
在数轴上表示为：
故答案为：D．
4．在以下回收、绿色食品、节能、节水四个标志中，是中心对称图形的是（ ）
A． B． C． D．
【答案】C
【分析】根据中心对称图形的概念：一个图形沿某个点旋转180度后能与原图完全重合的；由此问题可求解．
【详解】解：选项A、B、D不能找到一个点绕其旋转180度后能与原图完全重合，所以都不是中心对称图形，而C选项可以找到一个点绕其旋转180度后能与原图完全重合，所以是中心对称图形；
故选C．
【点睛】本题主要考查中心对称图形，熟练掌握中心对称图形的概念是解题的关键．
5．据共青团中央2023年5月3日发布的中国共青团团内统计公报，截至2022年12月底，全国共有共青团员7358万．数据7358万用科学记数法表示为（ ）
A．7.358×107B．7.358×103C．7.358×104D．7.358×106
【答案】A
【分析】本题主要考查了科学记数法，表示较大的数，利用科学记数法的法则解答即可．
【详解】解：7358万，
故选：A．
6．如图，的半径为5，弦，则的长为（ ）

A．1B．2C．3D．4
【答案】C
【分析】本题考查了垂径定理，由于于点C，所以由垂径定理可得，在中，由勾股定理即可得到答案．熟练运用垂径定理并结合勾股定理是解答本题的关键．
【详解】解：∵，
∴，
在中，，
由勾股定理可得：．
故选：C．
7．如图所示几何体的俯视图是（ ）

A． B． C． D．
【答案】D
【分析】根据俯视图是从上面看到的图形判定即可．
【详解】解：从上面看得该几何体的俯视图是：
．
故选：D．
【点睛】此题主要考查了简单组合体的三视图；用到的知识点为：主视图，左视图，俯视图分别是从物体的正面，左面，上面看得到的图形．
8．如图，在“经典诵读”比赛活动中，某校10名学生参赛成绩如图所示，对于这10名学生的参赛成绩，下列说法错误的是（ ）

A．众数是90分B．方差是10C．平均数是91分D．中位数是90分
【答案】B
【分析】根据众数、中位数、平均数、方差的定义和统计图中提供的数据分别列出算式，求出答案．
【详解】解：A、∵90出现了5次，出现的次数最多，∴众数是90；故此选项不符合题意；
B、方差是：；故此选项符合题意；
C、平均数是（85×2+100×1+90×5+95×2）÷10＝91；故此选项不符合题意；
D、∵共有10个数，∴中位数是第5、6个数的平均数，∴中位数是（90+90）÷2＝90；故此选项不符合题意．
故选：B．
【点睛】此题考查了折线统计图，用到的知识点是众数、中位数、平均数、方差，能从统计图中获得有关数据，求出众数、中位数、平均数、方差是解题的关键．
9．如图，正方形的对角线交于点O，M是边上一点，连接，过点O作交于点N，若四边形的面积是4，则的长为（ ）
A．2B．C．4D．
【答案】C
【分析】本题考查正方形的判定和性质，全等三角形的判定和性质．过点O作，证明，进而得到四边形的面积等于正方形的面积，进而求出的长，即可得解．
【详解】解：过点O作于点E，于点F，
则：，
∵四边形是正方形，
∴，
∴，四边形为矩形，
∴四边形为正方形，
∴，
∵，
∴，
∴，
∴，
∴正方形的面积等于四边形的面积，
∴，
∴（负值已舍掉）；
∴；
故选：C．
10．抛物线的对称轴是直线，抛物线与x轴的一个交点在点和点之间，其部分图象如图所示，下列结论①；②；③关于x的方程有两个不相等实数根；④当时，y随x增大而增大；⑤；⑥y的最小值为．其中正确的个数是（ ）

A．2个B．3个C．4个D．5个
【答案】B
【分析】本题考查了的图象与性质，根据对称轴确定抛物线与x轴的另一个交点，补全图象是解题关键．
【详解】解：∵抛物线的对称轴是直线，
∴，
∴，
即：，故①正确；
∵抛物线与x轴的一个交点在点和点之间，对称轴是直线，
∴抛物线与x轴的另一个交点在点和点之间，
补全图象如下：

∴当时，，故②正确；
由图象可知：抛物线与直线有两个交点，
故关于x的方程有两个不相等实数根，故③正确；
由图象可知：当时，y随x增大而减小，故④错误；
∵图象开口向下，
∴
∵，
∴
结合抛物线与x轴的两个交点范围可知，抛物线与轴负半轴相交，
∴，
∴，故⑤错误；
由图象可知：y的最大值为，故⑥错误；
故选：B
第Ⅱ卷
二、填空题（本大题共8个小题，每小题3分，共24分）
11．因式分解： ．
【答案】
【分析】此题考查了多项式分解因式，正确掌握因式分解的方法是解题的关键．利用提公因式法和平方差公式分解因式即可．
【详解】解：
故答案为：．
12．若在实数范围内有意义，则的取值范围是 ．
【答案】
【分析】此题主要考查了二次根式有意义的条件，正确掌握相关定义是解题关键．直接利用二次根式有意义则被开方数大于或等于零即可得出答案．
【详解】解：在实数范围内有意义，
故，
解得：．
故答案为：．
13．圆锥的底面半径是，母线长，则它的侧面展开图的圆心角的度数为 ．
【答案】
【分析】设圆锥的侧面展开图的圆心角为，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到，然后解关于的方程即可．
【详解】解：设圆锥的侧面展开图的圆心角为，
根据题意得
解得，
即圆锥的侧面展开图的圆心角为．
故答案为：．
【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
14．如图，直线，将含有角的三角形板的直角顶点C放在直线b上，若，则的度数为 ．

【答案】/18度
【分析】如图，过B作直线a的平行线，则直线，，根据，计算求解即可．
【详解】解：如图，过B作直线a的平行线，

∵直线，
∴直线，
∴，
∵，
∴，
故答案为：．
【点睛】本题考查了平行线的性质．解题的关键在于明确角度之间的数量关系．
15．若关于x的一元二次方程有两个不相等的实数根，实数m的取值范围是 ．
【答案】/
【分析】利用方程有两个不相等的实数根时，，建立关于m的不等式，求出m的取值范围．
【详解】解：关于x的一元二次方程有两个不相等的实数根，
，即，
解得：，
故答案为：．
【点睛】本题考查了根的判别式，牢记“当时，方程有两个不相等的实数根”是解题的关键．
16．如图所示，在平行四边形中，点在上，且，则 ．

【答案】
【分析】本题考查了平行四边形的性质、相似三角形的判定和性质等知识，设，，，则，利用相似三角形的性质求出平行四边形的面积，即可解决问题，解题的关键是学会利用参数解决问题．
【详解】解：设，，，则，
∵四边形是平行四边形，
∴，，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
故答案为:．
17．《九章算术》中记载：“今有人共买羊，人出五，不足四十五；人出七，不足三．问人数、羊价各几何？”译文：“今有人合伙买羊，若每人出五钱，还差四十五钱；若每人出7钱，还差三钱．问合伙人数、羊价各是多少？”设合伙人数为x人，羊价为y钱，可列方程组为 ．
【答案】
【分析】根据“若每人出5钱，还差45钱；若每人出7钱，还差3钱”中的等量关系分别列二元一次方程，即可求解．
【详解】解：设合伙人数为x人，羊价为y元，
依据“若每人出5钱，还差45钱”得：5x+45=y，
依据“若每人出7钱，还差3钱”得：7x+3=y，
因此可列方程组为：，
故答案为：．
【点睛】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键．
18．《九章算术》是中国古代的数学专著，书中记载了这样一个问题：“今有勾五步，股十二步，问勾中容方几何？”其大意是：如图，的两条直角边的长分别为5和12，则它的内接正方形的边长为 ．
【答案】/
【分析】先设正方形的边长为x，再表示出，，然后说明∽，并根据对应边成比例得出答案.
【详解】根据题意可知，．
设正方形的边长为x，则，.
∵四边形是正方形，
∴．
∵，
∴∽，
∴，
即，
解得.
所以正方形的边长为.
故答案为：.
【点睛】本题主要考查了正方形的性质，相似三角形的性质和判定，相似三角形的对应边成比例是求线段长的常用方法．
三、解答题（本大题共8个小题，第19、20、21题每题6分，第22、23题每题8分，第24、25题每题10分，第26题12分，共66分）
19．计算：
【答案】
【分析】直接利用零指数、绝对值、立方根、特殊角的函数化简计算即可．
【详解】解：
．
【点睛】本题考查了实数的运算，解题的关键是掌握零指数、绝对值、立方根、特殊角函数值，熟练计算．
20．先化简，再求值：，其中．
【答案】，．
【分析】原式第二项变形后约分，然后通分并利用同分母分式的减法法则计算得到最简结果，将x的值代入计算即可求出值．
【详解】解：原式=
=
=
当时，原式=.
【点睛】此题考查了分式的化简求值，分式的加减运算关键是通分，通分的关键是找最简公分母；分式的乘除运算关键是约分，约分的关键是找公因式．
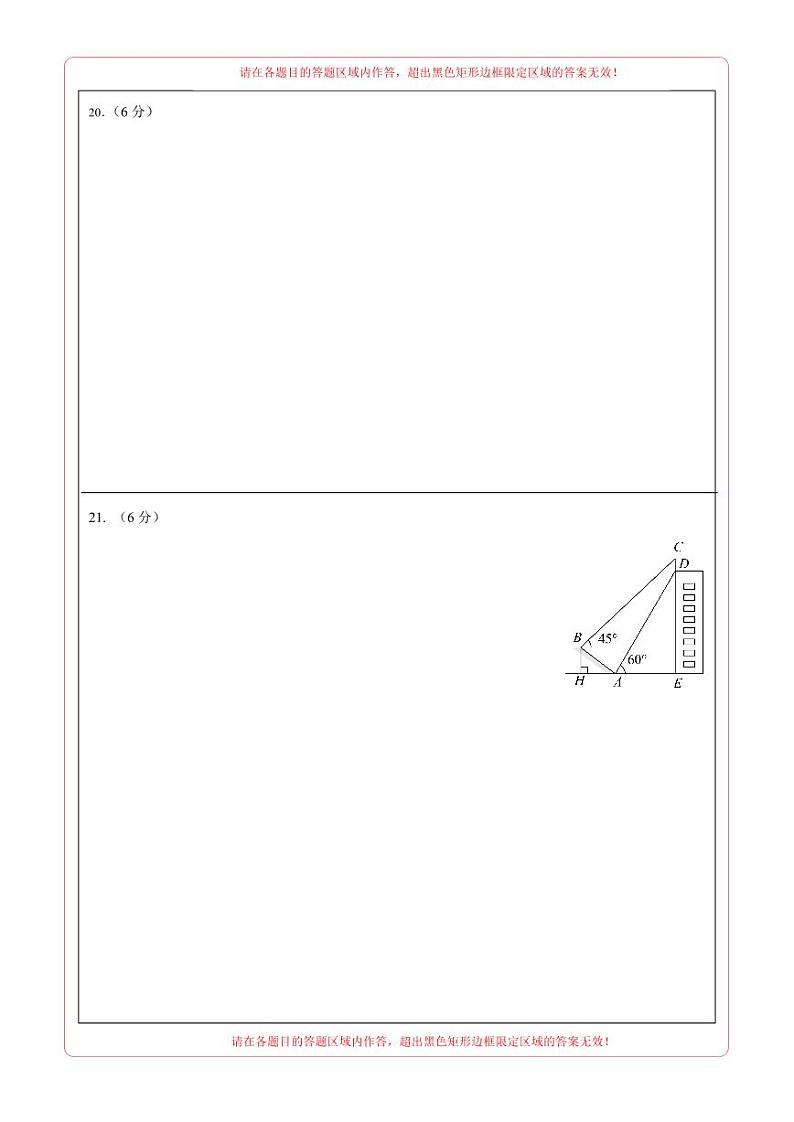
21．如图，某大楼的顶部树有一块广告牌，小李在山坡的坡脚处测得广告牌底部的仰角为．沿坡面向上走到处测得广告牌顶部的仰角为，已知山坡的坡度，米，米．

(1)求点距水平面的高度；
(2)求广告牌的高度．
【答案】(1)米；
(2)广告牌的高度约为米．
【分析】（1）在中，通过解直角三角形求出、即可；
（2）过作于在解直角三角形求出的长，进而可求出即的长，在中，，则，由此可求出的长，然后根据即可求出广告牌的高度．
【详解】（1）解：在中，
∴，
∴米；
（2）过作于，
如图所示：

由（1）得：
米， 米，
中，，
∴米，
中，，米，
∴米，
∴
米
答：广告牌的高度约为米．
【点睛】此题综合考查了仰角、坡度的定义，能够正确地构建出直角三角形，将实际问题化归为解直角三角形的问题是解答此类题的关键．
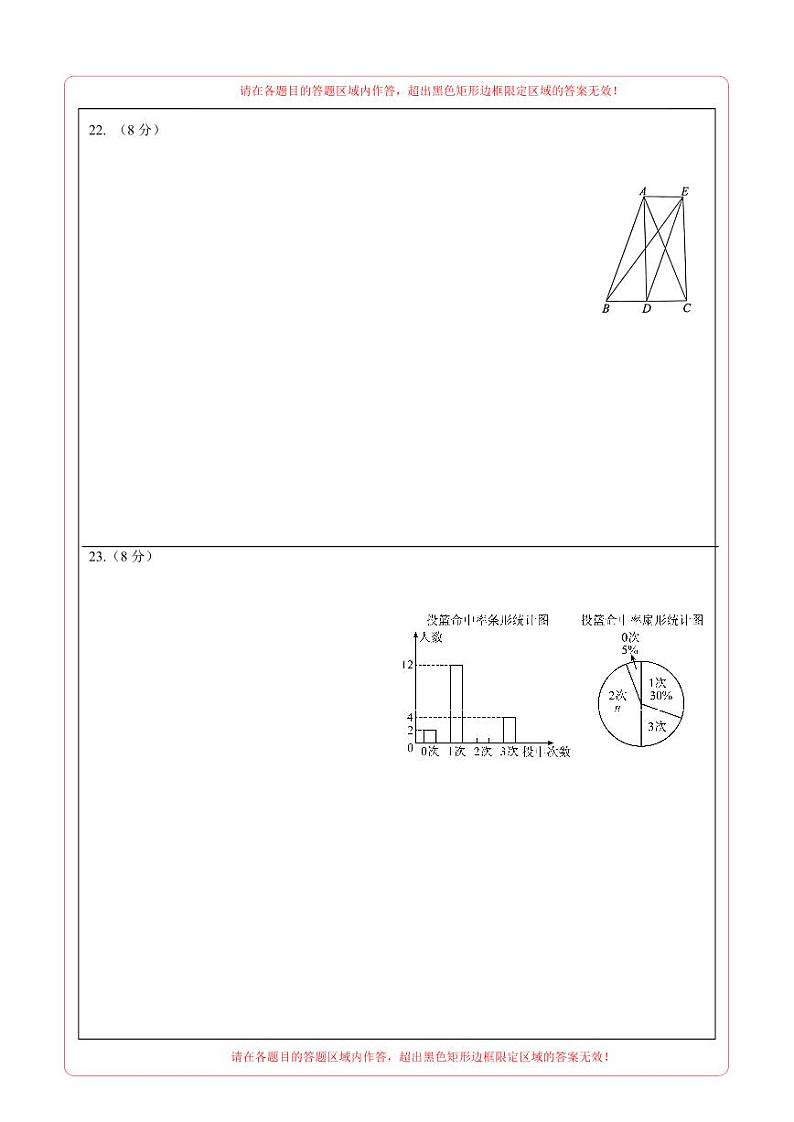
22．如图，在中，，点为中点，过点分别作的平行线，相交于点．
(1)求证：四边形为矩形；
(2)连接，若，求的长．
【答案】(1)见详解
(2)
【分析】（1）先根据平行四边形的判定，证明四边形是平行四边形，再根据矩形的判定，证明即可；
（2）根据矩形的性质，三角函数，及勾股定理即可得出结果．
【详解】（1）证明：由题意得，
四边形是平行四边形，
，点为中点，
，即，
四边形为矩形；
（2）解：∵四边形为矩形，
，
∵点为中点，
在中，，
解得：
在中，，
故的长为．
【点睛】本题考查了矩形的判定与性质，平行四边形的判定与性质，等腰三角形的性质，平行线的性质，熟练掌握定理与性质是解题的关键．
23．为了解九年级学生的投篮命中率，组织了九年级学生定点投篮，规定每人投篮3次．现对九年级（1）班每名学生投中的次数进行统计，绘制成如下的两幅统计图，根据图中提供的信息，回答下列问题．

(1)九年级（1）班的学生人数 人，扇形统计图中 %；
(2)扇形统计图中“3次”对应的圆心角的度数为 °；
(3)在投中3次的学生中，有2个男生2个女生，现要抽调两名学生参加学校投篮比赛，请用画树状图或列表的方法，求恰好抽到一男一女的概率．
【答案】(1)40，55
(2)36
(3)
【分析】（1）根据投中1次的人数及所占百分数求总人数，求出投中2次的人数，除以总人数即可求出所占的百分数；
（2）求出投中3次的人数所占比例，乘以360度即可；
（3）画树状图表示出所有等可能的情况，再从中找出抽到一男一女的情况数，利用概率公式求解．
【详解】（1）解：九年级（1）班的学生人数（人），
投中2次的人数为：（人），
扇形统计图中，
故答案为：40，55；
（2）解：扇形统计图中“3次”对应的圆心角的度数为：，
故答案为：36；
（3）解：画树状图如下：

由图可知，共有12种等可能的情况，其中恰好抽到一男一女的情况有8种，
，
即恰好抽到一男一女的概率是．
【点睛】本题考查条形统计图、扇形统计图、列表或画树状图法求概率，解题的关键是将条形统计图与扇形统计图间的信息进行关联，掌握列表或画树状图法求概率的原理．
24．如图，在平面直角坐标系中，的边在轴上，轴，点的坐标为，将向下方平移，得到，且点的对应点落在反比例函数的图象上，点的对应点落在轴上，连接．

(1)求证：四边形为平行四边形；
(2)求反比例函数的表达式；
(3)求平移的距离及线段扫过的面积．
【答案】(1)见解析
(2)
(3)5，24
【分析】（1）利用平移的性质，可得出，由轴且在轴上，可得出，结合，可得出，由，可得出，再利用“两组对边分别平行的四边形是平行四边形”，可证出四边形为平行四边形；
（2）连接，易证四边形是平行四边形，利用平行四边形的性质，可得出，结合，可得出三点共线，易证四边形是平行四边形，利用平行四边形的性质，可得出的长，结合，可得出点的坐标，再利用反比例函数系数的几何意义，可求出的值，进而可得出反比例函数的表达式；
（3）连接，在中，利用勾股定理，可求出的长，由此可得出平移的距离为，由，可得出四边形是平行四边形，再利用平行四边形的性质及三角形的面积公式，即可求出线段扫过的面积．
【详解】（1）证明：由平移的性质，得：，
轴，且在轴上，
，
．
，
，
四边形为平行四边形；
（2）解：连接，如图所示．

四边形为平行四边形，
，
又，
四边形是平行四边形，
，
，
三点共线．
轴，在轴上，，
四边形是平行四边形，
．
点的坐标为，
，
点的坐标为．
点在反比例函数的图象上，
，
反比例函数的表达式为；
（3）解：连接，如图所示．

在中，，
，
平移的距离为
，
四边形是平行四边形，
，
线段扫过的面积为．
【点睛】本题是反比例函数的综合题，考查了平移的性质、平行四边形的判定与性质、平行线的性质、反比例函数系数的几何意义、勾股定理以及三角形的面积，解题的关键是：由平移的性质及平行线的性质，找出及；（2）利用平移的性质及平行四边形的性质，找出点的坐标；（3）利用勾股定理及平行四边形的性质，求出的长及平行四边形的面积．
25．如图，在中，，是的直径，交于点D，过点D的直线交于点E，交的延长线于点P，是的切线．

(1)求的度数；
(2)若，，求图1中阴影部分的周长；
(3)如图2，若，连接，交于点N，若，求的值．
【答案】(1)
(2)
(3)
【分析】（1）根据直径所对的圆周角为直角进行解答即可；
（2）证明是等边三角形，可得，再由弧的长度，在中，求出，，则阴影部分的周长为；
（3）连接，，过作于点，利用同弧所对的圆周角相等，得到，设，则，求出，由得：，证明，得出，即可求出．
【详解】（1）解：∵是的直径，
∴，
∴．
（2）解：连接，如图所示：

∵，
∴，
∵是的切线，
∴，
∴，，
又∵，
∴，
∴，
∴，
∴是等边三角形．
∴，
∴弧的长度，
在中，，，
∴，
∴，
∴阴影部分的周长为：．
（3）解：连接，，过作于点，如图所示：

∵，
∴设，则，，
由得：，
∵，，
∴，
∴，
∴，
∴，
∴．
【点睛】本题考查圆的综合应用，熟练掌握圆的性质，切线的性质，弧长公式，同弧所对的圆周角相等，直径所对的圆周角为直角，三角形相似的判定及性质，平行线的性质是解题的关键．
26．定义：在平面直角坐标系中，抛物线与轴的交点坐标为，那么我们把经过点且平行于轴的直线称为这条抛物线的极限分割线．
【特例感知】
(1)抛物线的极限分割线与这条抛物线的交点坐标为______ ．
【深入探究】
(2)经过点和的抛物线与轴交于点，它的极限分割线与该抛物线另一个交点为，请用含的代数式表示点的坐标．
【拓展运用】
(3)在（2）的条件下，设抛物线的顶点为，直线垂直平分，垂足为，交该抛物线的对称轴于点．
①当时，求点的坐标．
②若直线与直线关于极限分割线对称，是否存在使点到直线的距离与点到直线的距离相等的的值？若存在，直接写出的值；若不存在，请说明理由．
【答案】(1)和
(2)点的坐标为
(3)①顶点为或顶点为；②存在，或或
【分析】（1）根据定义，确定c值，再建立方程组求解即可．
（2）把点代入解析式，确定，根据定义建立方程求解即可．
（3）①根据等腰直角三角形的性质，得到等线段，再利用字母表示等线段建立绝对值等式计算即可．
②设与对称轴的交点为，用含的式子表示出点的坐标，分别写出极限分割线、直线及直线的解析式，用含的式子分别表示出点到直线的距离和点到直线的距离，根据点到直线的距离与点到直线的距离相等，得出关于的绝对值方程，解方程即可．
【详解】（1）∵抛物线的对称轴为直线，极限分割线为，
极限分割线与这条抛物线的一个交点坐标为，则另一个交点坐标为．
故答案为： 和．
（2）抛物线经过点，
∴
∴
∴，
解得
∴点D的坐标为．
（3）①设与对称轴交于点，若，则．

∵点C的坐标为，点D的坐标为．．
∴，
∴，
∴，
解得．
∵抛物线的顶点为，
∴抛物线的顶点为，
∴当时，，故顶点为；
∴当时，，故顶点为；
∴顶点为或顶点为．
存在，或或．
如图，设与对称轴的交点为．

由知，，抛物线的顶点为，∴抛物线的极限分割线：，
直线垂直平分，
∴直线：，
∴点到直线的距离为；
直线与直线关于极限分割线对称，
直线： ，
∵，
∴点到直线的距离为，
点到直线的距离与点到直线的距离相等，
∴，
∴或，
解得或或，
故或或．
【点睛】．查了抛物线与坐标轴的交点坐标和直线与抛物线的交点坐标等知识点，明确题中的定义、熟练掌握二次函数的图像与性质及绝对值方程是解题的关键．