江西省抚州市第一中学2022-2023学年高二下学期第一次月考数学试卷(含答案)

这是一份江西省抚州市第一中学2022-2023学年高二下学期第一次月考数学试卷(含答案)，共18页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．已知等比数列,,,则( )
A.B.C.D.2
2．随机变量X服从正态分布,且,则下列说法一定正确是( )
A.B.C.D.
3．下列随机事件中的随机变量X服从超几何分布的是( )
A. 将一枚硬币连抛3次,记正面向上的次数为X
B. 某射手的射击命中率为0.8,现对目标射击1次,记命中的次数为X
C.从7男3女共10名学生干部中选出5名学生干部,记选出女生的人数为X
D.盒中有4个白球和3个黑球,每次从中摸出1个球且不放回,记第一次摸出黑球时摸取的次数为X
4．南宋数学家杨辉的重要著作《详解九章算法》中的“垛积术”问题介绍了高阶等差数列.以高阶等差数列中的二阶等差数列为例,其特点是从数列中的第二项开始,每一项与前一项的差构成等差数列.若某个二阶等差数列的前4项为:2,3,6,11,则该数列的第15项为( )
A.196B.197C.198D.199
5．投掷一枚质地均匀的骰子两次,记两次的点数均为奇数,两次的点数之和为4,则( )
A.B.C.D.
6．已知等比数列的前n项和为,若,,则( )
A.40B.30C.13D.50
7．如图,某建筑工地搭建的脚手架局部类似于一个的长方体框架,一个建筑工人欲从A处沿脚手架攀登至B处,则其最近的行走路线中不连续向上攀登的概率为( )
A.B.C.D.
8．裴波那契数列,因数学家莱昂纳多·裴波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,该数列满足,且．卢卡斯数列是以数学家爱德华·卢卡斯命名,与裴波那契数列联系紧密,即,且,则( )
A.B.C.D.
二、多项选择题
9．以下关于独立性检验的说法中,正确的是( )
A.独立性检验得到的结论一定正确
B.样本不同,独立性检验的结论可能有差异
C.独立性检验不是判断两分类变量是否相关的唯一方法
D.若随机变量,我们有99%以上的把握说吸烟与患肺病有关,则某人吸烟,那么他有99%的可能患有肺病
10．已知递增的正整数列的前n项和为．以下条件能得出为等差数列的有( )
A.B.
C.D.
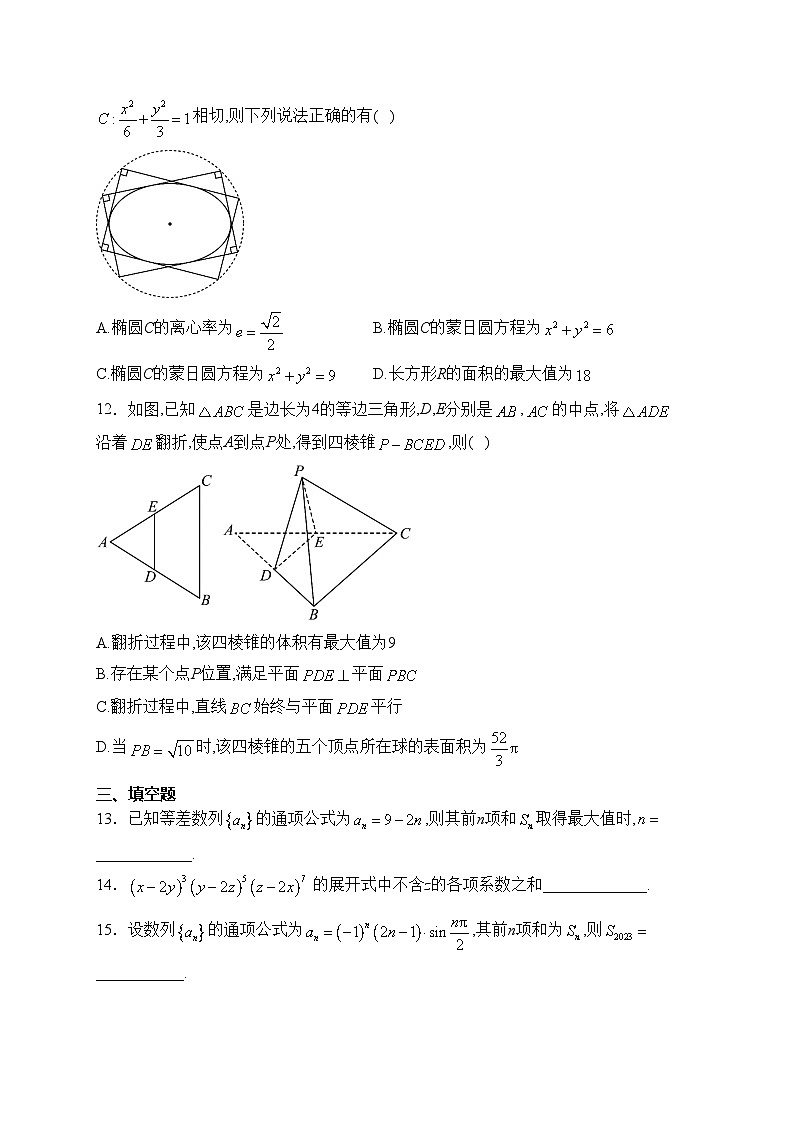
11．“蒙日圆”涉及几何学中的一个著名定理,该定理的内容为：椭圆上任意两条互相垂直的切线的交点,必在一个与椭圆同心的圆上.称此圆为该椭圆的“蒙日圆”,该圆由法国数学家加斯帕尔•蒙日最先发现,已知长方形R的四条边均与椭圆相切,则下列说法正确的有( )
A.椭圆C的离心率为B.椭圆C的蒙日圆方程为
C.椭圆C的蒙日圆方程为D.长方形R的面积的最大值为
12．如图,已知是边长为4的等边三角形,D,E分别是,的中点,将沿着翻折,使点A到点P处,得到四棱锥,则( )
A.翻折过程中,该四棱锥的体积有最大值为9
B.存在某个点P位置,满足平面平面
C.翻折过程中,直线始终与平面平行
D.当时,该四棱锥的五个顶点所在球的表面积为
三、填空题
13．已知等差数列的通项公式为,则其前n项和取得最大值时,____________.
14． 的展开式中不含z的各项系数之和_____________.
15．设数列的通项公式为,其前n项和为,则___________.
16．已知双曲线的左右焦点分别为,,若C与直线有交点,且双曲线上存在不是顶点的P,使得,则双曲线离心率取值范围范围为_______________.
四、解答题
17．已知等差数列的公差为2,且,,成等比数列,
（1）求的通项公式;
（2）记,若数列的前n项和.
18．如图,在以A,B,C,D,E,F为顶点的六面体中（其中平面）,四边形是正方形,平面,且平面平面.
（1）设M为棱的中点,证明;
（2）若,,求平面与平面的锐二面角的余弦值.
19．已知正项数列的前n项和为,且,(且).
（1）求数列的通项公式;
（2）求数列的前n项和.
20．某企业计划新购买100台设备,并将购买的设备分配给100名年龄不同（视为技术水平不同）的技工加工一批模具,因技术水平不同而加工出的产品数量不同,故产生的经济效益也不同.若用变量x表示不同技工的年龄,变量y为相应的效益值（元）,根据以往统计经验,他们的工作效益满足最小二乘法,且y关于x的线性回归方程为.
（1）试根据r的值判断使用该批设备的技工人员所产生的效益与技工年龄的相关性强弱（则认为y与x线性相关性很强;则认为y与x线性相关性不强）;
（2）若这批设备有A,B两道独立运行的生产工序,且两道工序出现故障的概率依次是0.02,0.03.若两道工序都没有出现故障,则生产成本不增加;若A工序出现故障,则生产成本增加2万元;若B工序出现故障,则生产成本增加3万元;若A,B两道工序都出现故障,则生产成本增加5万元.求这批设备增加的生产成本的期望.
参考数据: ;
参考公式：回归直线的斜率和截距的最小二乘估计分别为,,,.
21．已知椭圆一个顶点,以椭圆E的四个顶点为顶点的四边形面积为．
（1）求椭圆E的方程;
（2）过点的直线l斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与直线交交于点M,N,当时,求k的取值范围．
22．口袋中共有7个质地和大小均相同的小球,其中4个是黑球,现采用不放回抽取方式每次从口袋中随机抽取一个小球,直到将4个黑球全部取出时停止.
（1）记总的抽取次数为X,求;
（2）现对方案进行调整：将这7个球分装在甲乙两个口袋中,甲袋装3个小球,其中2个是黑球;乙袋装4个小球,其中2个是黑球.采用不放回抽取方式先从甲袋每次随机抽取一个小球,当甲袋的2个黑球被全部取出后再用同样方式在乙袋中进行抽取,直到将乙袋的2个黑球也全部取出后停止.记这种方案的总抽取次数为Y,求并从实际意义解释与（1）中的的大小关系.
参考答案
1．答案：A
解析：设公比为q,
因,,所以,所以,
所以.
故选：A.
2．答案：B
解析：因为,
由正态分布的对称性可得,故B正确,A错误,
而正态分布的方差无法确定,故C,D均错误.
故选：B．
3．答案：C
解析：对于A选项,将一枚硬币连抛3次,记正面向上的次数为X,
则X服从二项分布,A不满足;
对于B选项,某射手的射击命中率为0.8,现对目标射击1次,记命中的次数为X,则X服从两点分布,B不满足;
对于C选项,从7男3女共10名学生干部中选出5名学生干部,记选出女生的人数为X,
则X服从超几何分布,C满足;
对于D选项,盒中有4个白球和3个黑球,每次从中摸出1个球且不放回,
记第一次摸出黑球时摸取的次数为X,则X不服从超几何分布,D不满足.
故选：C.
4．答案：C
解析：若某个二阶等差数列的前4项为:2,3,6,11,
即,,,,
可知,,,…,,
累加即可得到,
则,则
故选:C.
5．答案：C
解析：由题意,共9个基本事件,
其中和为4的只有和两个事件,
所以．
故选：C．
6．答案：A
解析：由于是等比数列,所以,,,也成等比数列,
其中,,所以,,
所以.
故选：A.
7．答案：B
解析：从A的方向看,行走方向有三个：左、前、上. 从A到B的最近的行走线路,需要向左三次,向前两次,向上三次,共8次.所以从A到B的最近的行走线路,总的方法数有种.
不连续向上攀登的安排方法是：先将向左、向前的安排好,再对向上的方法进行插空.故方法数有：.
所以最近的行走路线中不连续向上攀登的概率为.
故选：B.
8．答案：C
解析：因为,
所以当时,,
所以,
故,
因为,
所以,,
故,
所以.
故选：C.
9．答案：BC
解析：利用独立性原理检验时,与样本的选取有关,因此得到的结论可能有误,A错误;
样本不同,独立性检验的结论可能有差异,B正确;
可以利用等高堆积条形图直观地反映两个分类变量之间是否具有关联性,
因此独立性检验不是判断两分类变量是否相关的唯一方法,C正确;
若,则有99%以上的把握说吸烟与患肺病有关,某人吸烟,不表示他有99%的可能患有肺病,D错误.
故选：BC.
10．答案：AC
解析：对于A,时,,
当时,满足,
而且时,,则等差数列,A正确;
对于B,,当时,不满足上式,
得,因此数列不是等差数列,B错误;
对于C,,即为隔项等差数列,且是递增的正整数列,
则,,,且,有,即,
于是,,因此,
所以为等差数列,C正确;
对于D,,,
,,即数列是以为首项,2为公比的等比数列,,则,
从到中间恰有项：,,,它们是递增的正整数,
而到中间有个递增的正整数,无法一一对应,
若,则会出现如：2,4,5,8,9,10,11,16…的数列,非等差数列,D错误.
故选：AC.
11．答案：ACD
解析：椭圆C的离心率为,
设两条互相垂直的切线的交点为,
当题设中的两条互相垂直的切线中有斜率不存在或斜率为0时,可得点P的坐标是,或.
当题设中的两条互相垂直的切线中的斜率均存在且均不为0时,可设点P的坐标是,（,且）,
所以可设曲线C的过点P的切线方程是.
由,得,
由其判别式的值为0,得,
因为,（,为过P点互相垂直的两条直线的斜率）是这个关于k的一元二次方程的两个根,
所以,
由此,得,
即C的蒙日圆方程为：;
因为蒙日圆为长方形的外接圆,设,,
则矩形面积公式为,显然,
即矩形四条边都相等,为正方形时,.
故选:ACD.
12．答案：CD
解析：如图1,设M,N分别是,的中点,连接,,
则,,,且,
对于A项,当平面平面时,四棱锥的体积最大,
的高为,四边形为高为的梯形,
梯形面积,
体积,故A项错误;
对于B项,设平面平面,
因为,平面,平面,故平面,
而平面,则,
因为,,则有,,
则为平面与平面所成的二面角,
由可知,,所以不可能为直角,
即平面与平面所成的二面角不可能为直二面角,故B项错误;
对于C项,因为D,E分别是,的中点,所以,
又平面,平面,
所以平面,即翻折过程中,直线始终与平面平行,故C正确;
对于D项,当时,由,可知,即,
又,且,,平面,则平面,
又平面,则平面平面,
设四棱锥的外接球球心为O,的外心为G,则平面,
如图2,易知点M为等腰梯形的外心,则平面,
则四边形为矩形,且,
从而有,
从而该四棱锥的五个顶点所在球的表面积为,故D项正确.
故选：CD.
13．答案：4
解析：令,得,
又,所以当时,,当时,,
所以当前n项和取得最大值时,.
故答案为：4.
14．答案：128
解析：利用二项展开式的通项公式进行展开,
设项为,项为n,项为m.
展开后得对每一项进行合并得 ,因为展开式中不含z,所以,又得取值为,n得取值为,故得,,
代入展开式得,又k得取值为,
分别带入后各项系数之和为.
故答案为：128.
15．答案：2024
解析：当,时,,;
当,时,,;
当,时,,;
当,时,,.
,
.
.
故答案为：2024.
16．答案：
解析：双曲线C与直线有交点,则,,解得,
双曲线上存在不是顶点的P,使得,则P点在右支上,
设与y轴交于点Q,由对称性,所以,
所以,
,
所以,由得,所以,
又中,,,
所以,即,
综上,．
故答案为：．
17．答案：（1）
（2）
解析：（1）由题知
即解得,
所以.
（2）
.
18．答案：（1）证明见解析
（2）
解析：（1）因为M为棱的中点,,所以,
又平面平面,平面平面,平面,
所以平面,
又因平面,所以;
（2）如图以点D为原点建立空间直角坐标系,
连接,由于四边形ABCD是正方形,所以,
又平面,平面,所以,
又平面,所以,
,,,,,设,
由,,,
得,解得,,故,
则,,,
设平面,的法向量分别为,,
则 即,取,则 ,
即,取,则 ,
则,
所以平面与平面的锐二面角的余弦值.
19．答案：（1）
（2）
解析：（1）,
,
又,
,
数列是以为首项,1为公差的等差数列,
, ,
当时,,
当时,,满足上式,
数列的通项公式为;
（2）由（1）可知,,
,
当时,．
20．答案：（1）使用该批设备的技工人员所产生的的效益与技工年龄的相关性强
（2）0.13万元
解析：（1）由题得,,
所以,
所以,
因,所以y与x线性相关性很强,
所以使用该批设备的技工人员所产生的的效益与技工年龄的相关性强;
（2）设增加的生产成本为（万元),则的可能取值为0,2,3,5,
,
,
,
,
所以（万元),
所以这批设备增加的生产成本的期望为0.13万元.
21．答案：（1）;
（2）．
解析：（1）因为椭圆过,故,
因为四个顶点围成的四边形的面积为,故,即,
故椭圆的标准方程为：.
（2）设,,
因为直线的斜率存在,故,
故直线,令,则,同理.
直线,由可得,
故,解得或.
又,,故,所以
又
故即,
综上,或.
22．答案：（1）
（2）6,答案见解析
解析：（1）X可能取值为4,5,6,7,
,
,
,
;
（2）Y可能取值为4,5,6,7,设甲袋和乙袋抽取次数分别为和,
,
,
,
,
.
在将球分装时,甲袋中的黑球取完后直接取乙袋,若此时甲袋中还有其它球,则该球的干扰作用已经消失,所以同样是要取出4个黑球,调整后的方案总抽取次数的期望更低.