宁夏中卫市中宁县2022_2023学年高一数学上学期10月线上测试试题含解析

这是一份宁夏中卫市中宁县2022_2023学年高一数学上学期10月线上测试试题含解析，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 集合A={0，2，4，6}的子集个数是（）
A. 8B. 12C. 15D. 16
【答案】D
【解析】
【分析】根据集合中元素个数即可得到结果.
【详解】∵集合A中含有4个元素，
∴集合A子集个数为：，
故选：D
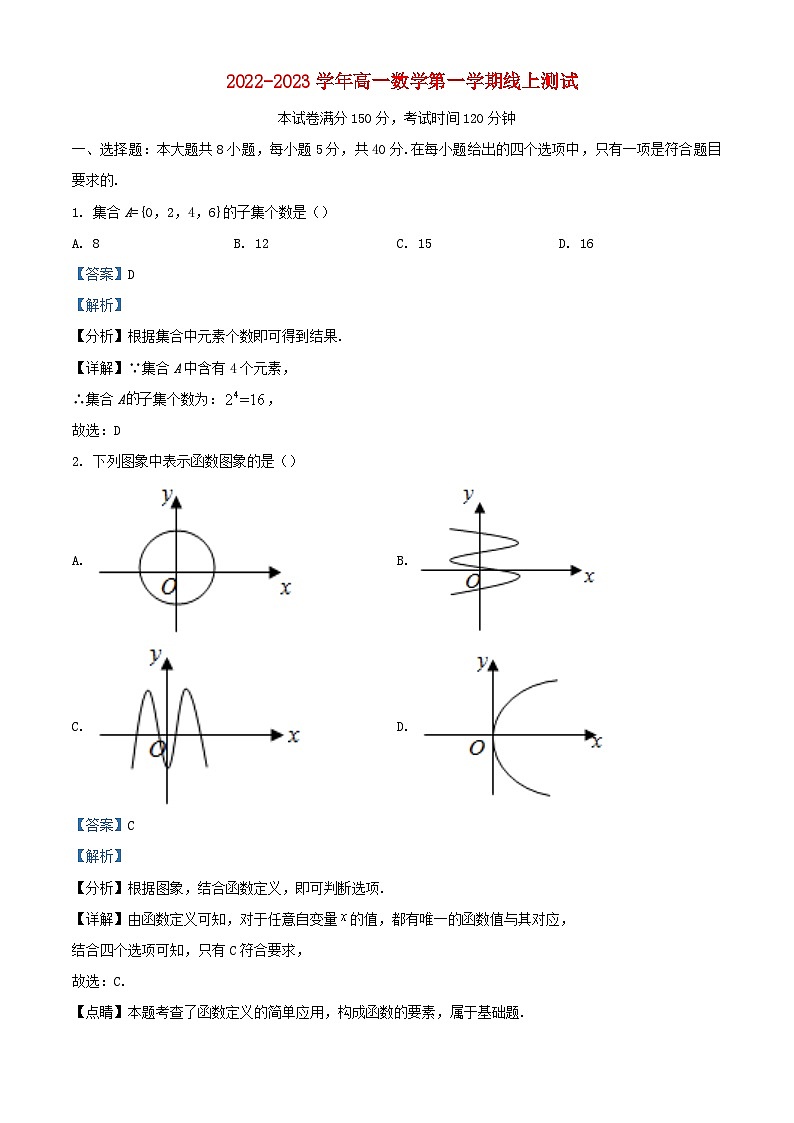
2. 下列图象中表示函数图象的是（）
A. B.
C. D.
【答案】C
【解析】
【分析】根据图象，结合函数定义，即可判断选项.
【详解】由函数定义可知，对于任意自变量的值，都有唯一的函数值与其对应，
结合四个选项可知，只有C符合要求，
故选：C.
【点睛】本题考查了函数定义的简单应用，构成函数的要素，属于基础题.
3. 已知实数、、，且，则下列不等式正确的是
A. B. C. D.
【答案】C
【解析】
【分析】利用特值可进行排除，由不等式性质可证明C正确.
【详解】若a＝1，b＝﹣1，则A，B错误，若c＝0，则D错误，
∵a＞b，
∴a+1＞a＞b＞b﹣1，
∴a+1＞b﹣1，故C正确，
故选C．
【点睛】本题主要考查不等式与不等关系，在限定条件下，比较几个式子的大小，可用特殊值代入法，属于基础题．
4. 若函数，则（）．
A. B. C. D.
【答案】B
【解析】
【分析】根据题意，由函数的解析式可得，计算可得答案．
【详解】解：根据题意，函数，
则，
故选：．
5. 下列各组函数中，表示同一函数的是（）
A. ，B. ，
C. ，D. ，
【答案】C
【解析】
【分析】逐项判断各选项中与的定义域、解析式是否完全相同即可判断两函数是否相等.
【详解】A选项，与定义域相同但解析式不同，不是同一函数；
B选项，的定义域为，，解析式相同但定义域不同，不是同一函数；
C选项，，与定义域、解析式均相同，为同一函数；
D选项，定义域为，，两函数解析式相同但定义域不同，不是同一函数.
故选：C
【点睛】本题考查函数的概念、相等函数的判断，属于基础题.
6. 若，则的最小值是（）
A. 0B. 2C. D. 3
【答案】D
【解析】
分析】根据基本不等式即可得到结果.
【详解】∵，
∴，
当且仅当，即时，等号成立，
∴的最小值是3，
故选：D
7. 设，则“”是“”的（）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】D
【解析】
【分析】根据小充分，大必要即可得到答案.
【详解】由可得或，
由可得，
由或推不出，由不能推出或，
所以“”是“”的既不充分也不必要条件，
故选：D
8. 不等式的解集为（）
A. B. C. D.
【答案】D
【解析】
【分析】
原不等式可转化为，求解即可.
【详解】由知：，即有且，解得，
故选：D
二、选择题：本大题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分.
9. 如图是函数的图像，则下列说法正确的是（）
A. B. 的定义域为
C. 的值域为D. 若，则或2
【答案】CD
【解析】
【分析】结合函数的图像和定义域，值域等性质进行判断即可．
【详解】由图像值，故A错误；
函数的定义域为，，故B错误；
函数的值域为，，故C正确；
若，则或2，故正确
故选：．
10. 已知函数，分别由下表给出：则方程的解可以表示为（）
A. 1B. 2C. 3D. 4
【答案】BD
【解析】
【分析】根据表格中的对应关系，由外及内即可.
【详解】∵，∴，
∴或4.
故选：BD
11. 已知，，且，则（）
A. 的最小值为3B. 的最小值为4
C. 的最小值为4D. 的最小值为2
【答案】BC
【解析】
【分析】根据基本不等式，巧用“1”即可得到结果.
【详解】∵，，且，
∴，
当且仅当时等号成立，∴的最小值为4，A错B对；
同样，
当且仅当时等号成立，∴的最小值为4，D错C对；
故选：BC
12. 已知关于x的不等式的解集为，则（）
A. B.
C. D. 不等式的解集为
【答案】ABD
【解析】
【分析】根据不等式的解集判断的关系，判断ABC的正误，然后根据参数间的关系将不等式转化为，求得解集即可.
【详解】由题知，方程的两个根为，4，且，故A正确；
由韦达定理知，，解得，，故B正确；
，故C错误；
不等式等价于，即，
解得解集为，故D正确；
故选：ABD
三、填空题：本大题共4小题，每小题5分，共20分.
13. 设，则________．
【答案】
【解析】
【分析】分别令，，由集合元素具有互异性可确定结果.
【详解】若，则，不符合集合元素互异性；
若，解得：（舍）或，则，满足题意；
综上所述：.
故答案为：.
14. 命题p：，则命题p的否定为__.
【答案】
【解析】
【分析】根据特称命题否定的方法，否定量词也否定结论，可得答案.
【详解】∵命题p：，
∴命题p的否定为：，
故答案为：
15. 若，，则的取值范围为__________.
【答案】
【解析】
【分析】根据条件，得到的范围，然后与的范围相加，得到的取值范围.
【详解】因为，可得，所以
又
由不等式的基本性质可得：
故答案为：
【点睛】本题考查不等式的性质，属于基础题.
16. 已知，那么___________.
【答案】##
【解析】
【分析】设，利用换元法可求得的表达式，即可得解.
【详解】设，则，所以，，则.
故答案为：.
四、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤.
17. 已知全集，，.求：
（1）；
（2）
【答案】（1）
（2）
【解析】
【分析】根据交并补运算即可得到结果.
【小问1详解】
∵，，，
∴；
【小问2详解】
∵，，
∴，，
∴
18. 如图，公园的管理员计划在一面墙的同侧，用彩带围成四个相同的长方形区域.若每个区域的面积为24，要使围成四个区域的彩带总长最小，则每个区域的长和宽分别是多少米？求彩带总长的最小值.
【答案】每个区域的长是米，宽是米时，彩带总长的最小，且最小值为，
【解析】
【分析】
先设每个区域长和宽分别，，并由题意得到，彩带总长为，再利用基本不等式求的最小值，最后判断等号成立的条件并作答.
【详解】设每个区域的长和宽分别，，由题意有：，彩带总长为，
由基本不等式：，
当且仅当即，时，取等号，
所以每个区域的长是米，宽是米时，彩带总长的最小，且最小值为，
【点睛】本题考查利用基本不等式解决实际问题，是基础题
19. 已知函数的定义域为集合，．
（1）求集合；
（2）若“x∈A”是“x∈B”的充分条件，求的取值范围.
【答案】（1）A＝{x|－2（2）.
【解析】
【分析】（1）由算术平方根的被开方数大于等于0，分式的分母不等于0可求得集合A；
（2）由已知得A⊆B，由此可得的取值范围.
【小问1详解】
解：函数表达式有意义，即，
解得，即A＝{x|－2【小问2详解】
解：因为A＝{x|－2所以.
20. 已知集合，.
（1）若，求；
（2）若，求实数的取值范围.
【答案】（1）；（2）
【解析】
【分析】
（1）若，则集合，可求；
（2）若，则，解不等式组则实数的取值范围可求．
【详解】解：（1）若，集合，．
则；
（2）若，则，即，
实数的取值范围是．
21. 已知二次函数满足且．
（1）求的解析式；
（2）求函数在区间上的值域．
【答案】（1）；（2）．
【解析】
【分析】（1）设二次函数，由已知建立方程组，解之可求得函数的解析式；
（2）运用配方法得，再根据二次函数的性质可求得答案.
【详解】解：（1）设二次函数，
∵，∴，∴；
又∵，
∴且，∴，；∴．
（2）∵，
∴在区间上，当时，函数有最小值；
当时，函数有最大值；
∴在区间上的值域是．
22. 已知不等式的解集为
（1）求，的值；
（2）解不等式.
【答案】（1），
（2）答案见解析
【解析】
【分析】（1）依题意可得或是方程的根，利用韦达定理得到方程组，解得即可；
（2）由（1）可得原不等式可化为，再对参数分类讨论，即可得解；
【小问1详解】
解：因为不等式的解集为或，
所以或是方程的根，
根据韦达定理，
解得，
【小问2详解】
解：由（1）可知不等式化为，
即
当时，不等式的解集为，
当时，不等式的解集为，
当时，不等式的解集为
1
2
3
4
3
4
1
2
4
3
2
3