初中数学4.2 平行四边形练习

这是一份初中数学4.2 平行四边形练习，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共10小题，共30.0分）
如图，矩形ABCD的对角线AC，BD交于点O，AB=6，BC=8，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为( )
A. 485
B. 325
C. 245
D. 125
如图，将矩形ABCD折叠，使点C和点A重合，折痕为EF，EF与AC交于点O.若AE=5，BF=3，则AO的长为( )
A. 5B. 325C. 25D. 45
如图，在矩形ABCD中，AB=2，BC=3，两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则当OC为最大值时，点C的坐标为( )
A. (332,32)
B. (32,12)
C. (233,12)
D. (233,32)
如图，点E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点．则下列说法：①若AC=BD，则四边形EFGH是菱形；②若AC⊥BD，则四边形EFGH是矩形；③若四边形EFGH是平行四边形，则AC与BD互相平分：④若四边形EFGH是正方形，则AC与BD互相垂直且相等．其中正确的个数是( )
A. 1B. 2C. 3D. 4
如图1，菱形ABCD中，，动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B，同时动点Q以每秒2个单位的速度自点B出发沿折线运动到点图2是点P、Q运动时，的面积S随时间t变化关系图象，则a的值是
A. 2B. 2.5C. 3D. 23
在菱形ABCD中，∠ABC=60°，AB=1，E为边BC的中点．则对角线BD上的动点P到E、C两点的距离之和的最小值为( )
A. 34B. 33C. 32D. 3
如图，在△ABC中，∠ACB=90°，边BC在x轴上，顶点A，B的坐标分别为(-2,6)和(7,0).将正方形OCDE沿x轴向右平移，当点E落在AB边上时，点D的坐标为( )
A. (32,2)
B. (2,2)
C. (114,2)
D. (4,2)
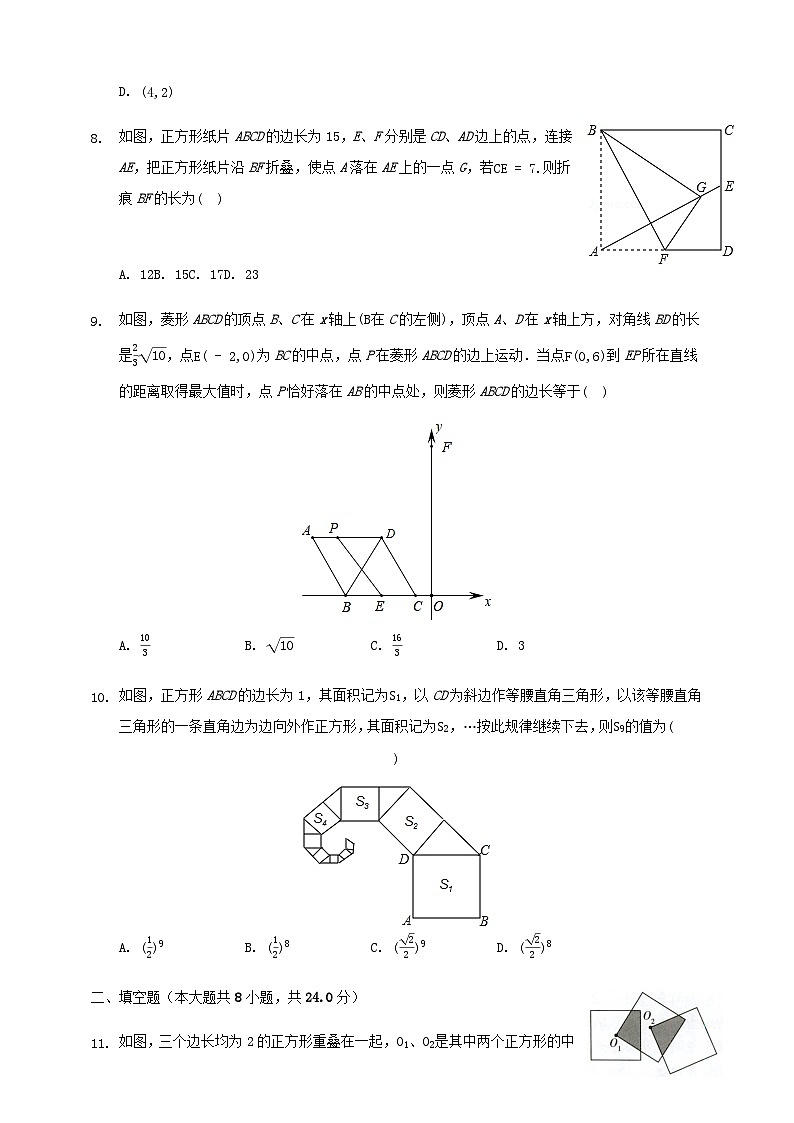
如图，正方形纸片ABCD的边长为15，E、F分别是CD、AD边上的点，连接AE，把正方形纸片沿BF折叠，使点A落在AE上的一点G，若CE=7.则折痕BF的长为( )
A. 12B. 15C. 17D. 23
如图，菱形ABCD的顶点B、C在x轴上(B在C的左侧)，顶点A、D在x轴上方，对角线BD的长是2310，点E(-2,0)为BC的中点，点P在菱形ABCD的边上运动．当点F(0,6)到EP所在直线的距离取得最大值时，点P恰好落在AB的中点处，则菱形ABCD的边长等于( )
A. 103B. 10C. 163D. 3
如图，正方形ABCD的边长为1，其面积记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积记为S2，…按此规律继续下去，则S9的值为( )
A. (12)9B. (12)8C. (22)9D. (22)8
二、填空题（本大题共8小题，共24.0分）
如图，三个边长均为2的正方形重叠在一起，O1、O2是其中两个正方形的中心，则阴影部分的面积是________．
如图，将两条宽度均为2的纸条相交成30°角叠放，则重合部分构成的四边形ABCD的面积为______ ．
如图，线段AB的长为63cm，点D在线段AB上，△ACD为等边三角形，过点D作DP⊥CD，点G是射线DP上不与点D重合的一动点，作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段OB长度的最小值等于______ cm．
如图，在矩形ABCD中，AB=5，AD=8，点E是边AD上的一个动点，把△BAE沿BE折叠，点A落在A'处，如果A'恰在矩形的某条对称轴上，则AE的长为______．
如图，菱形纸片ABCD中，∠A=60°，点P是AB边的中点，折叠纸片，使点C落在直线DP上的C处，折痕为经过点D的线段DE.则∠DEC的度数为______．
如图，将边长为8的正方形纸片ABCD沿着EF折叠，使点C落在AB边的中点M处．点D落在点D'处，MD'与AD交于点G，则△AMG的内切圆半径的长为______．
如图，将长方形ABCD(纸片)折叠，使点B与AD边上的点K重合，EG为折痕；点C与AD边上的点K重合，FH为折痕．已知∠1=67.5°，∠2=75°，EF=3+1，则BC的长为______．
某同学在数学活动课上做如下操作(如图所示)：第一步：作一个正方形ABCD；第二步：分别取AD，BC的中点M，N，连接MN；第三步：以点N为圆心，ND长为半径画弧，交BC的延长线于E；第四步：过E作EF⊥AD，交AD的延长线于F，则CECD的值是 ．
三、解答题（本大题共6小题，共46.0分）
如图，在矩形ABCD中，F是BC边上一点，AF的延长线交DC的延长线于点G，DE⊥AG，垂足为E，且DE=DC，求证：BF=AE．
如图，正方形ABCD，点E，F分别在边AD，CD上，且DE=CF，AF与BE相交于点G．
(1)求证：BE=AF；
(2)若AB=4，DE=1，求AG的长．
如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．
(1)求证：BD=CD；
(2)如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．
如图所示，AD//BC，∠BAD=90°，以B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C作CF⊥BE于点F．
(1)线段BF与图中哪条线段相等？写出来并加以证明：
(2)若AB=12，BC=13，P从E沿ED方向运动，Q从C出发向B运动，两点同时出发且速度均为每秒1个单位．
①当t=______秒时，四边形EPCQ是矩形；
②当t=______秒时，四边形EPCQ是菱形．
如图，有一张长方形纸条ABCD，AB=10cm，BC=4cm，点M，N分别在边AB，CD上，现将四边形BCNM沿MN折叠，使点B，C分别落在点B'，C'上，边MB'与边CD交于点E．
(1)如图(1)，若折叠后，点B与点D重合，求此时DN的长度；
(2)如图(2)，若CN=2cm，当△AMN是等腰三角形时，求此时四边形BCNM的面积；
(3)如图(3)，若CN=3cm，在点M从点A向点B运动的过程中，则点E相应运动的路径长为 cm．
如图1，在平面直角坐标系中，直线L2：y=-12x+6与L1：y=12x交于点A，分别与x轴、y轴交于点B、C．
(1)分别求出点A、B、C的坐标；
(2)若D是线段OA上的点，且△COD的面积为12，求直线CD的函数表达式；
(3)在(2)的条件下，设P是射线CD上的点．
①如图2，过点P作PQ//OC，且使四边形OCPQ为菱形，请直接写出点Q的坐标；
②在平面内是否存在其它点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．
答案和解析
1.【答案】C
解：∵AB=6，BC=8，
∴矩形ABCD的面积为48，AO=DO=12AC=5，
∵对角线AC，BD交于点O，
∴△AOD的面积为12，
∵EO⊥AO，EF⊥DO，
∴S△AOD=S△AOE+S△DOE，即12=12AO×EO+12DO×EF，
∴12=12×5×EO+12×5×EF，
∴5(EO+EF)=24，
∴EO+EF=245，
故选：C．
2.【答案】C
解：∵矩形ABCD，
∴AD//BC，AD=BC，AB=CD，
∴∠EFC=∠AEF，
∴AE=AF=3，
由折叠得，FC=AF，OA=OC，
∴BC=3+5=8，
在Rt△ABF中，AB=52-32=4，
在Rt△ABC中，AC=42+82=45，
∴OA=OC=25，
故选：C．
3.【答案】A
解：E为AB的中点，当O，E及C共线时，OC最大，过C作CF⊥x轴于F，则∠CFO=90°，
此时OE=BE=12AB=1，由勾股定理得：CE=BC2+BE2=2，
OC=1+2=3，
即BE=12CE，
∵∠CBE=90°，
∴∠ECB=30°，∠BEC=60°，
∵OE=EB
∴∠EOB=∠EBO=30°
∴CF=12OC=32
由勾股定理得：OF=OC2-CF2=32-(32)2=332，
所以点C的坐标是(332,32).
故选A．
4.【答案】C
解：∵点E，F，G，H分别是四边形ABCD边AB，BC，CD，DA的中点，
∴HG//AC//EF，HG=EF=12AC，
∴四边形ABCD的中点四边形EFGH是平行四边形，故③错误；
∵点E，F，G，H分别是四边形ABCD边AB，BC，CD，DA的中点，
∴EH//BD//GF，EH=GF=12BD，
∴当对角线BD=AC时，EF=FG，此时中点四边形EFGH是菱形，故①正确；
当对角线AC⊥BD时，EF⊥FG，此时中点四边形EFGH是矩形，故②正确；
当对角线AC=BD且AC⊥BD时，EF=FG且EF⊥FG，此时中点四边形EFGH是正方形，故④正确．
∴正确的说法有3个．
故选：C．
5.【答案】D
解：由图2得，t=4时两点停止运动，
∴点P以每秒1个单位速度从点A运动到点B用了4秒
∴AB=4
∵点Q运动到点C之前和之后，△BPQ面积算法不同，即t=2时，S的解析式发生变化
∴图2中点M对应的横坐标为2，
此时P为AB中点，点C与点Q重合，
如图，连接AC，
∵菱形ABCD中，AB=BC=4，∠B=60°
∴△ABC是等边三角形
∴CP⊥AB，BP=12AB=2
∴CP=BC2-BP2=42-22=23，
∴a=S=12BP⋅CP=12×2×23=23
故选：D．
6.【答案】C
解：连接AC、AE，AE交BD于P，则此时PE+PC最小，连接CP，
∵菱形ABCD，
∴OA=0C，AC⊥BD，AB=BC，
A和C关于BD对称，
∴AP=CP，
∵∠ABC=60°，
∴△ABC是等边三角形，
∴AC=AB=1，
∵E为边BC的中点，
∴AE⊥BC，
∴∠BAE=30°，
∴BE=12，
根据勾股定理得：AE=32，
∴PE+PC=AE=32．
故选C．
7.【答案】B
解：如图，设正方形D'C'O'E'是正方形OCDE沿x轴向右平移后的正方形，
∵顶点A，B的坐标分别为(-2,6)和(7,0)，
∴AC=6，OC=2，OB=7，
∴BC=9，
∵四边形OCDE是正方形，
∴DE=OC=OE=2，
∴O'E'=O'C'=2，
∵E'O'⊥BC，
∴∠BO'E'=∠BCA=90°，
∴E'O'//AC，
∴△BO'E'∽△BCA，
∴E'O'AC=BO'BC，
∴26=BO'9，
∴BO'=3，
∴OC'=7-2-3=2，
∴当点E落在AB边上时，点D的坐标为(2,2)，
故选：B．
8.【答案】C
解：∵四边形ABCD为正方形，
∴AB=AD=15，∠BAD=∠D=90°，
∵CE=7，
∴DE=15-7=8，
由折叠及轴对称的性质可知，△ABF≌△GBF，BF垂直平分AG，
∴BF⊥AE，AH=GH，
∴∠BAH+∠ABH=90°，
又∵∠FAH+∠BAH=90°，
∴∠ABH=∠FAH，
在△ABF与△DAE中
∠BAF=∠ADEAB=AD∠ABF=∠DAE,
∴△ABF≌△DAE(ASA)，
∴AF=DE=8，BF=AE，
在Rt△ABF中，
BF=AB2+AF2=225+64=17，
故选C．
9.【答案】A
解：如图1中，当点P是AB的中点时，作FG⊥PE于G，连接EF．
∵E(-2,0)，F(0,6)，
∴OE=2，OF=6，
∴EF=22+62=210，
∵∠FGE=90°，
∴FG≤EF，
∴当点G与E重合时，FG的值最大．
如图2中，当点G与点E重合时，连接AC交BD于H，PE交BD于J.设BC=2a．
∵PA=PB，BE=EC=a，
∴PE//AC，BJ=JH，
∵四边形ABCD是菱形，
∴AC⊥BD，BH=DH=103，BJ=106，
∴PE⊥BD，
∵∠BJE=∠EOF=∠PEF=90°，
∴∠EBJ=∠FEO，
∴△BJE∽△EOF，
∴BEEF=BJEO，
∴a210=1062，
∴a=53，
∴BC=2a=103，
故选：A．
10.【答案】B
解：在图中标上字母E，如图所示．
∵正方形ABCD的边长为1，△CDE为等腰直角三角形，
∴DE2+CE2=CD2，DE=CE，
∴S2+S2=S1．
观察，发现规律：S1=12=1，S2=12S1=12，S3=12S2=14，S4=12S3=18，…，
∴Sn=(12)n-1．
当n=9时，S9=(12)9-1=(12)8，
故选：B．
11.【答案】2
解：如图，连结O1B、O1C
．∵∠BO1F+∠FO1C=90∘，∠FO1C+∠CO1G=90∘，
∴∠BO1F=∠CO1G，
∵四边形ABCD是正方形，∴∠O1BF=∠O1CG=45∘．
在△O1BF和△O1CG中，∠FO1B=∠CO1G,BO1=CO1,∠FBO1=∠GCO1,
∴△O1BF≌△O1CG(ASA)，
∴前两个正方形重叠部分的面积是14S正方形，
同理，后两个正方形重叠部分的面积也是14S正方形，∴S阴影部分=12S正方形=2．
12.【答案】8
解：过点A作AE⊥BC于E，AF⊥CD于F，如图所示：
∵两条纸条宽度相同，
∴AE=AF，
∵AB//CD，AD//BC，
∴四边形ABCD是平行四边形，∠ABC=30°，
∵S▱ABCD=BC⋅AE=CD⋅AF，
又∵AE=AF，
∴BC=CD，
∴四边形ABCD是菱形，
∴AB=BC，
在Rt△AEB中，∠AEB=90°，∠ABC=30°，AE=2，
∴BC=AB=2AE=2，
∴四边形ABCD的面积=BC⋅AE=4×2=8，
故答案为：8．
13.【答案】33
解：连接AO，
∵四边形CDGH是矩形，
∴CG=DH，OC=12CG，OD=12DH，
∴OC=OD，
∵△ACD是等边三角形，
∴AC=AD，∠CAD=60°，
在△ACO和△ADO中，
AC=ADAO=AOCO=DO，
∴△ACO≌△ADO(SSS)，
∴∠OAB=∠CAO=12×60°=30°，
∴点O一定在∠CAB的平分线上运动，所以当OB⊥AO时，OB的长最小，
∵∠OAB=30°，∠AOB=90°，
∴OB=12AB=12×63=33(cm)，
即OB的最小值为33cm，
故答案为：33．
14.【答案】52或533
解：分两种情况：
①如图1，过A'作MN//CD交AD于M，交BC于N，
则直线MN是矩形ABCD的对称轴，
∴AM=BN=12AD=4，MN=AB=5，
∵△ABE沿BE折叠得到△A'BE，
∴A'E=AE，A'B=AB=5，
∴A'N=52-42=3，
∴A'M=MN-A'N=5-3=2，
由勾股定理得：A'E2=EM2+A'M2，
∴A'E2=(4-A'E)2+22，
解得：A'E=52，
∴AE=52；
②如图2，过A'作PQ//AD交AB于P，交CD于Q，
则直线PQ是矩形ABCD的对称轴，
∴PQ⊥AB，AP=PB，AD//PQ//BC，
∴A'B=2PB，
∴∠PA'B=30°，
∴∠A'BC=30°，
∴∠EBA'=30°，
∴AE=A'E=33A'B=533；
综上所述：AE的长为52或533，
故答案为：52或533．
15.【答案】75°
解：连接BD，如图所示：
∵四边形ABCD为菱形，
∴AB=AD，∠C=∠A=60°，
∴△ABD为等边三角形，∠ADC=120°，
∵P为AB的中点，
∴DP为∠ADB的平分线，即∠ADP=∠BDP=30°，
∴∠PDC=90°，
∴由折叠的性质得：∠CDE=∠PDE=45°，
在△DEC中，∠DEC=180°-(∠CDE+∠C)=75°．
故答案为：75°．
16.【答案】43
解：∵将边长为8的正方形纸片ABCD沿着EF折叠，使点C落在AB边的中点M处．
∴ME=CE，MB=12AB=4=AM，∠D'ME=∠C=90°，
在Rt△MBE中，ME2=MB2+BE2，
∴ME2=16+(8-ME)2，
∴ME=5
∴BE=3，
∵∠D'ME=∠DAB=90°=∠B
∴∠EMB+∠BEM=90°，∠EMB+∠AMD'=90°
∴∠AMD'=∠BEM，且∠GAM=∠B=90°
∴△AMG∽△BEM
∴AMBE=AGMB=GMME
∴43=AG4=GM5
∴AG=163，GM=203
∴△AMG的内切圆半径的长=AG+AM-GM2=43
故答案为：43
17.【答案】3+2+3
解：由题意，得：∠3=180°-2∠1=45°，∠4=180°-2∠2=30°，BE=KE、KF=FC，
如图，过点K作KM⊥BC于点M，
设KM=x，则EM=x、MF=3x，
∴x+3x=3+1，
解得：x=1，
∴EK=2、KF=2，
∴BC=BE+EF+FC=EK+EF+KF=3+2+3，
∴BC的长为3+2+3，
故答案为：3+2+3．
18.【答案】5-12
解：在正方形ABCD中，取AB=2a，
∵N为BC的中点，
∴NC=12BC=a．
在Rt△DNC中，ND=NC2+CD2=5a．
又∵NE=ND，
∴CE=NE-NC=5-1a
∴CECD=5-12．
19.【答案】证明：在矩形ABCD中，AB=CD，BC//AD，∠B=90°，DE=CD，
∴AB=DE，∠BFA=∠EAD，
∵DE⊥AG，
∴∠AED=90°，
∴∠AED=∠B，
在△ABF与△DEA中
∠BFA=∠EAD∠B=∠AEDAB=DE，
∴△ABF≌△DEA，
∴BF=AE．
20.【答案】(1)证明：∵四边形ABCD是正方形，
∴∠BAE=∠ADF=90°，AB=AD=CD，
∵DE=CF，
∴AE=DF，
在△BAE和△ADF中，AB=AD ∠BAE=∠ADFAE=DF,
∴△BAE≌△ADF(SAS)，
∴BE=AF；
(2)解：由(1)得：△BAE≌△ADF，
∴∠EBA=∠FAD，
∴∠GAE+∠AEG=90°，
∴∠AGE=90°，
∵AB=4，DE=1，
∴AE=3，
∴BE=AB2+AE2=42+32=5，
在Rt△ABE中，12AB×AE=12BE×AG，
∴AG=3×45=125．
21.【答案】(1)证明：∵AF//BC，
∴∠AFE=∠DCE，
∵E是AD的中点，
∴AE=DE，
在△AEF和△DEC中，
∴△AEF≌△DEC，
∴AF=DC，
∵AF=BD，
∴BD=CD；
(2)解：四边形AFBD是矩形．
∵AB=AC，D是BC的中点，
∴AD⊥BC，
∴∠ADB=90°
∵AF=BD，
∵过A点作BC的平行线交CE的延长线于点F，即AF//BC，
∴四边形AFBD是平行四边形，
又∵∠ADB=90°，
∴四边形AFBD是矩形．
22.【答案】8 13
解：(1)BF=AE．
理由如下：
∵AD//BC，
∴∠CBF=∠AEB，
在△BCF和△EBA，
∠BFC=∠A∠CBF=∠AEBBC=EB，
∴△BCF≌△EBA，
∴BF=EA；
(2)EP=t，CQ=t，
在Rt△ABE中，AE=132-122=5，
∵EP=CQ，EP//CQ，
∴四边形EPCQ为平行四边形，
①当CP⊥AD时，∠CPE=90°，则平行四边形EPCQ为矩形，
此时AP=BC=13，即5+t=13，解得t=8，
即当t=8时，四边形EPCQ是矩形；
②作CH⊥AD于H，如图，
当CD=CQ=ED=t，平行四边形EPCQ为菱形，
而PD=t+5-13=t-8，
在Rt△PDC中，122+(t-8)2=t2，解得t=13，
即当t=13，四边形EPCQ是菱形．
故答案为：8，13．
23.【答案】解：(1)由折叠可知，BC=DC'=4cm，NC=NC'，
设DN=xcm，则NC=NC'=(10-x)cm，
在Rt△DNC'中，DN2=DC'2+NC'2，
即x2=42+(10-x)2，
解得：x=295，即DN=295cm；
(2)当△AMN是等腰三角形时，易知不存在NA=NM，
如图，当MA=MN时，
设BM=acm，则(10-a)2=42+(a-2)2，
解得：a=5，
则四边形BCNM的面积S=(2+5)×42=14(cm2)；
当AM=AN时，如图，
设BM=bcm，则AM=AN=(10-b)cm，
则(10-b)2=42+(10-2)2，解得b=10-45，
则四边形BCNM的面积S=(24-85)cm2．
综上所述，四边形BCNM的面积为(24-85)cm2或14cm2；
(3)解：如图，当点M与A重合时，易知AE=EN，设AE=EN=xcm，
在Rt△ADE中，则有x2=42+(10-x-3)2，解得x=6514，
∴DE=10-3-6514=3314(cm)；
如图，当点M运动到MB'⊥AB时，DE'的值最大，DE'=10-3-4=3(cm)，
如图3中，当点M运动到点B'落在CD时，
NB'=CN2+CB2=42+32=5(cm)，
DB'(即DE″)=10-3-5=2(cm)；
∴点E的运动轨迹E→E'→E″，运动路径=EE'+E'B'=3-3314+3-2=2314(cm)．
故答案为：2314⋅
24.【答案】解：(1)由y=-12x+6y=12x，解得x=6y=3，
∴A(6,3)．
∵y=-12x+6与分别与x轴、y轴交于点B、C，
∴C(0,6)，B(12,0)．
(2)设D(m,12m)，
由题意：OC=6，△COD的面积为12，
∴12×6×m=12，
∴m=4，
∴D(4,2)，∵C(0,6)，
设直线CD的解析式为y=kx+b，则有4k+b=2b=6，
解得k=-1b=6，
∴直线CD的解析式为y=-x+6．
(3)①∵四边形OCPQ是菱形，
∴OC=PC=6，
设P(m,-m+6)，
∴m2+m2=36，
∴m=32或-32，
∴P(32,-32+6)，
∵PQ//OC，PQ=OC，
∴Q(32,-32)，
②如图2-1中，当OC为菱形的对角线时，OC垂直平分线段OC，
易知P'(3,3)，Q'(-3,3)，
∴满足条件的点Q'的坐标为(-3,3)．