北师大版七年级上册2.9 有理数的乘方教学ppt课件

这是一份北师大版七年级上册2.9 有理数的乘方教学ppt课件，共36页。PPT课件主要包含了有理数的乘方，第2课时等内容，欢迎下载使用。
1.在现实背景中，理解有理数乘方的意义.2.正确理解乘方、幂、指数、底数等概念.3.掌握有理数乘方的运算方法.4.通过对乘方意义的理解，培养学生观察比较、分析、归纳概括的能力，渗透转化思想．
准备好了吗？一起去探索吧！
你知道世界上最高的山峰是什么山峰吗？
假如有一张足够大的纸，连续对折30次，它的厚度能超过珠穆朗玛峰吗？
你们是不是也会有这样的疑问：纸才多厚呢？怎么可能超过珠穆朗玛峰呢？
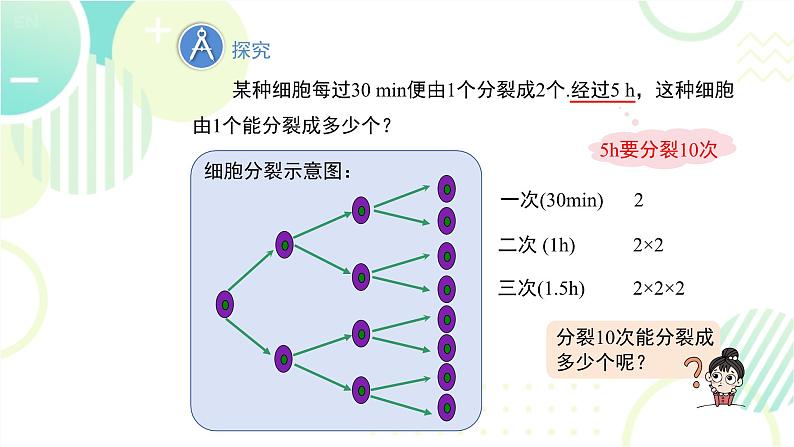
某种细胞每过30 min便由1个分裂成2个.经过5 h，这种细胞由1个能分裂成多少个？
分裂10次能分裂成多少个呢？
某种细胞每过30min便由1个分裂成2个，经过5h，这种细胞由1个能分裂成多少个？
可以简便地记作 210
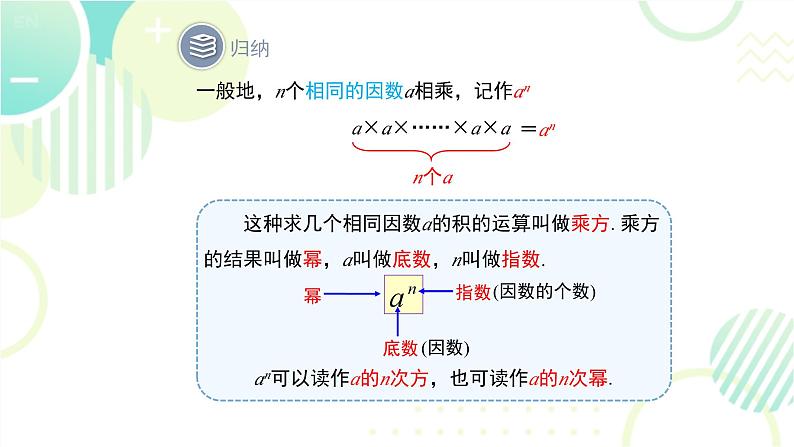
这种求几个相同因数a的积的运算叫做乘方.乘方的结果叫做幂，a叫做底数，n叫做指数.
一般地，n个相同的因数a相乘，记作an
an可以读作a的n次方，也可读作a的n次幂.
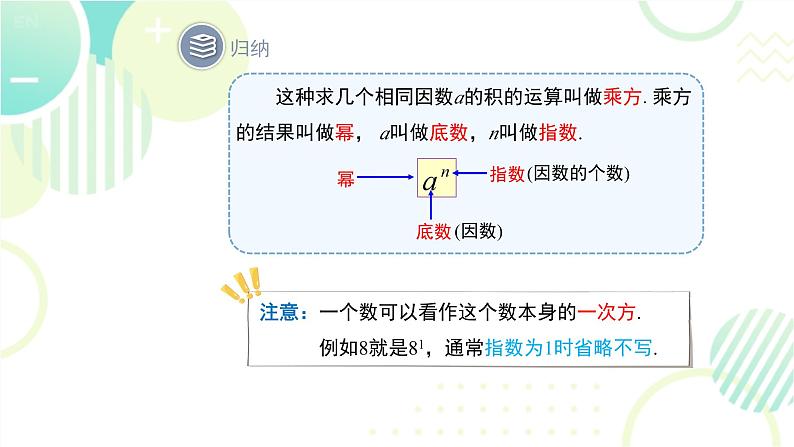
这种求几个相同因数a的积的运算叫做乘方.乘方的结果叫做幂， a叫做底数，n叫做指数.
注意：一个数可以看作这个数本身的一次方. 例如8就是81，通常指数为1时省略不写.
(1) 在(–6)3中，底数是_____，指数是_____.
(2) 在 中，底数是_____，指数是_____.
解： (1)53＝5×5×5＝125；
(1)53 ； (2)(-3)4； (3)
(2)(-3)4＝(-3)×(-3)×(-3)×(-3)＝81；
(-3)4和-34，它们的意义一样吗？
(-3)4 ＝(-3)×(-3)×(-3)×(-3) ，表示4个-3相乘；
-34 ＝-(3×3×3×3)，表示4个3相乘的相反数.
和 ，它们的意义一样吗？
，它的底数是 ，
总结：幂的底数是分数或负数时，底数应该添上括号！
(1)-(-2)3； (2)-24； (3)
解： (1)-(-2) 3 ＝-[(-2)×(-2)×(-2)]＝-(-8)＝8；
(2)-24＝-(2×2×2×2)＝-16；
利用有理数的乘法运算来进行有理数的乘方运算.
在-|-3|3，-(-3)3 ，(-3)3 ，-33中，最大的数是( )
A. -|-3|3 B. -(-3)3 C. (-3)3 D. -33
2.关于-74的说法正确的是( )A.底数是-7 B.表示4个-7相乘C.表示4个7相乘的相反数 D.表示7个-4相乘
1. (-1)2等于( ) A．-1 B．1 C．-2 D．2
3.下列说法中正确的是( ) A.23表示2×3的积 B.任何一个有理数的偶次幂都是正数 C.-32与(-3)2互为相反数 D.一个数的平方是 ，这个数一定是
求几个相同因数a的积的运算叫做乘方.
教科书第59页习题2.13第1、2、4题
1.在现实背景中，进一步加深对有理数乘方意义的理解；2.会根据一组数的特点，探究与乘方有关的规律性问题；3.通过实例感受当底数大于1时，乘方运算的结果增长得很快；4.培养学生认真思考、分析、解决问题的能力，切实提高学生的运算能力．
还记得有理数的乘方的定义吗？
一般地，n个相同的因数a相乘，记作an ，即
(1)102，103，104 ；(2)(-10)2 ，(-10)3，(-10)4 .
(-10)4＝(-10)×(-10)×(-10)×(-10)＝10000
解：(1)102＝10×10＝100
103＝10×10×10＝1000
104＝10×10×10×10＝10000
(2)(-10)2＝(-10)×(-10)＝100
(-10)3＝(-10)×(-10)×(-10)＝-1000
观察一下，底数为10的幂有什么规律？
-10的奇次幂是负数，-10的偶次幂是正数.
10的任何次幂都是正数.
你能总结出正数幂与负数幂的特点吗？
负数的奇次幂是负数， 负数的偶次幂是正数.
正数的任何次幂都是正数.
有一张厚度为0.1 mm的纸，将它对折1次后，厚度为2×0.1 mm.
22 ×0.1＝0.4(mm)
所以，这张纸对折2次后，厚度为0.4 mm.
(1) 对折2次后，厚度为多少毫米？
对折2次
对折1次
(2) 假设对折20次，厚度为多少毫米？
对折3次
对折20次
220层
220×0.1＝104857.6(mm)
104857.6 mm＝104.8576 m
所以，这张纸对折20次后，厚度为104857.6 mm.
104.8576 m＞90 m
哇！这张纸对折20次后比30层楼还要高呢.
当指数不断增加时，底数为2的幂的增长速度是很快的.
你见过拉面师傅拉面条吗？拉面师傅将一根粗面条拉长、两头捏合，再拉长、捏合，重复这样，就拉成许多根面条了，据报道，在一次比赛中，某拉面师傅用1 kg面粉拉出约209万根面条，你知道是怎样得出这个结果的吗？
≈106
21＝2
22＝4
22＝8
210＝1024
24＝16
≈103
那么221 ≈200万
所以，拉面师傅用1 kg面粉拉出约209万根面条，大约拉了21次.
(1)(-5)4 (2)(-5)5 (3)-(-5)6 (4)-(-5)7
判断下列各式结果的符号，你能发现什么规律？
负数的奇次幂是负数，负数的偶次幂是正数.
正数的相反数是负数，负数的相反数是正数.
1m长的木棒，第1次截去一半，第2次截去剩下部分的一半，如此截下去，第7次后剩下的木棒有多长？
每截取一次，总是剩下上一次的 .
答：第7次后剩下的木棒有 米.
(1) (2) (3)-53 (4)
(3)-53＝-125
22 -21＝2×211×21＝2123 -22＝2×221×22＝2(　)24 -23＝2×231×23＝2(　)……
请仔细观察，写出第4个等式；(2) 请你找规律，写出第n个等式.
25-24＝2×24-1×24＝24
2n+1-2n＝2×2n-1×2n＝2n
(1) ①的面积是____；②的面积是____； ③的面积是____；④的面积是____； ⑤的面积是____；⑥的面积是____；
3.如图，将一个边长为1的正方形纸片分割成6个部分，部分①是边长为1的正方形纸片面积的一半，部分②是部分①面积的一半，部分③是部分②面积的一半，依次类推.
(2) 受此启发，你能求出 的值吗？
当指数不断增加时，底数为2的幂的增长速度相当快.
教科书第62页习题2.14第1、3题