





数学北师大版5.2 求解一元一次方程教学课件ppt
展开
这是一份数学北师大版5.2 求解一元一次方程教学课件ppt,共58页。PPT课件主要包含了你还有别的解法吗,15x-28,x-2x8,移项要变号,例2解方程,合并同类项,解下列方程,解得x1080,+a-ba-b,x+05等内容,欢迎下载使用。
准备好了吗?一起去探索吧!
求解一元一次方程|移项
1.进一步熟悉利用等式的基本性质解一元一次方程的基本技能.2.在解方程的过程中分析、归纳移项法则,并能运用这一法则解方程.3.体会解一元一次方程中的转化思想.4.通过学生观察、独立思考等过程、培养学生归纳、概括的能力.
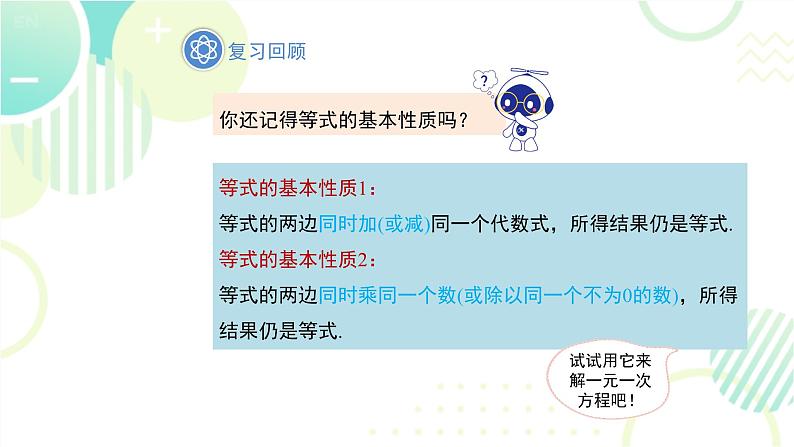
等式的基本性质1:等式的两边同时加(或减)同一个代数式,所得结果仍是等式.等式的基本性质2:等式的两边同时乘同一个数(或除以同一个不为0的数),所得结果仍是等式.
你还记得等式的基本性质吗?
试试用它来解一元一次方程吧!
利用等式的基本性质解下列方程:
解:方程两边同时加2,得 5x-2+2=8+2. 合并同类项,得 5x=10. 方程两边同除以5,得 x=2.
解:方程两边同时减3x,得 7x-3x=3x-8-3x. 合并同类项,得 4x=-8. 方程两边同除以4,得 x=-2.
(2)7x=3x-8.
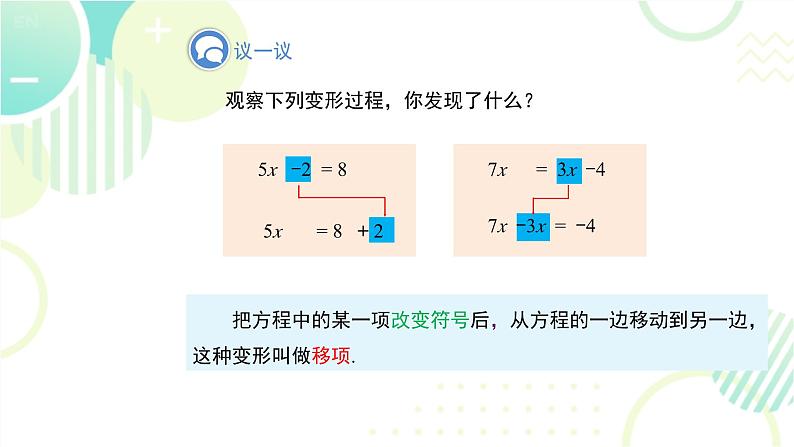
7x = 3x -4
7x -3x = -4
观察下列变形过程,你发现了什么?
把方程中的某一项改变符号后,从方程的一边移动到另一边,这种变形叫做移项.
下面的移项对不对?如果不对,应怎样改正?
(1)5+x=10移项得x= 10+5 ;(2)6x=2x+8移项得 6x=8 - 2x;(3)5-2x=4-3x移项得3x-2x=4-5;(4)-2x+7=1-8x移项得-2x+8x=1-7.
注意:交换两项位置≠移项.
移项时,应注意什么问题?
移项的依据是等式的基本性质;
通常把含有未知数的项移到方程左边,把常数项(不含未知数的项)移到方程右边.
利用移项的方法解下列方程:
(1)5x-2=8;
解:移项,得 5x=8+2. 化简,得 5x=10. 方程两边同除以5,得 x=2.
解:移项,得 7x-3x=-8. 合并同类项,得 4x=-8. 方程两边同除以4,得 x=-2.
例1 解下列方程.
(1) 2x+6=1; (2) 3x+3=2x+7.
(1) 可以利用等式的基本性质解,也可以利用移项方法解, 对比得到最简便的方法.
法一:两边同时减6,得 2x+6-6=1-6. 合并同类项,得 2x=-5. 方程两边同除以2,得 x=-2.5.
法二:移项,得 2x=1-6. 化简,得 2x=-5. 方程两边同除以2,得 x=-2.5.
(2) 直接利用移项的方法解,注意移项要变号.
移项,得 3x-2x=7-3.合并同类项,得 x=4.
直接利用移项的方法解,注意移项要变号,含未知数的移到左边,常数项移到右边.
移项,得 合并同类项,得方程两边同除以 ,得x=4.
方程两边同除以未知数的系数(系数化为1)
(1) 10x-3 = 9 ; (2)5x-2 = 7x+8;
解: 移项,得 10x = 9+3.
化简,得 10x= 12.
两边同时除以10,得
解: 移项,得 5x-7x = 8+2.
合并同类项,得 -2x= 10.
两边同时除以-2,得
(3) ; (4) .
解: 移项,得
合并同类项,得
两边同时乘以-2,得
合并同类项,得
两边同时乘以 ,得
2.下面方程的解法对吗?如果不对,应怎样改正?
解方程:-2x+5=4-3x 解:移项,得 3x-2x=4+5.合并同类项,得 x=9.
解:移项,得 -2x+3x=4-5. 合并同类项,得 x=-1.
3.某航空公司规定:乘坐飞机普通舱旅客每人最多可免费托运20kg行李,超过部分每千克按飞机票价的1.5%购买行李票,一名旅客托运了35kg行李,机票连同行李费共付1323元,求该旅客的机票票价.
解:设机票票价为x元,根据题意,得 x+(35-20)·x·1.5%=1323.
答:该旅客的机票票价为1080元.
①移项;②合并同类项;③系数化为1.
教科书 第136页习题5.3 第1、2题
2 求解一元一次方程第2课时
求解一元一次方程|去括号
1.能用去括号的方法求解一元一次方程,进一步体会解一元一次方程的基本步骤.2.会抓住实际问题中的等量关系列一元一次方程解决实际问题.3.体验用多种方法解一元一次方程,提高解一元一次方程的能力.4.通过对实际问题的探究,激发学生的学习兴趣和探究欲望,增强学习数学的兴趣.
括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变; 括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.
回想一下,去括号的法则是什么?
-(a-b)=-a+b
设1听果奶饮料x元,那么可列出方程 4(x+0.5)+x=10-3.
问题:一听果奶饮料多少钱?
这个方程列的对吗?为什么?
等量关系:买果奶饮料的钱+买可乐的钱=10元-3元
+ = 10-3
4(x+0.5)+x=10-3.
(y-0.5)+4y=10-3
设1听可乐y元,那么可列出方程
方程4(x+0.5)+x=10-3和(y-0.5)+4y=10-3与以前的方程有什么不同?
怎样去解这样的方程呢?
利用去括号法则,先去括号,再用上节课所学的求解过程就能解该方程了.
去括号的目的是能利用移项法解方程;其实质是乘法的分配律.
解方程:(1)4(x+0.5)+x=10-3, (2)(y-0.5)+4y=10-3.
去括号,得 4x+2+x=10-3.移项,得 4x+x=10-3-2.合并同类项,得 5x=5. 方程两边同除以5,得 x=1.
解:去括号,得 y-0.5+4y=10-3. 移项,得 y+4y=10-3+0.5. 合并同类项,得 5y=7.5.方程两边同除以5,得 y=1.5.
去括号,解一元一次方程的步骤是怎样的?
去括号解方程的步骤:①去括号;②移项;③合并同类项;④系数化为1.
例 解方程: -2(x-1)=4.
利用去括号解方程的方法,先去括号,移项,合并同类项,再系数化为1.
去括号,得 -2x+2=4 移项,得 -2x=4-2合并同类项,得 -2x=2 方程两边同除以-2,得x=-1.
可以先把括号前面的系数化为1,再移项,合并同类项求解.
方程两边同除以 –2,得 x-1=-2 移项,得 x=-2+1即 x=-1.
比较上面两种解法,说说它们的区别.
-2 (x-1) =4.
看做整体可解出它,进而解出x
解法2:先在方程两边同除以-2,使各项系数变小,且系数变为了正数,也渗透了整体思想,既简便又不会因符号问题而出现错误.
解法1:先去括号,然后解答,与解法二相比,较麻烦;
1.解方程1-2(x-1)=0,去括号正确的是( )A.1-2x-1=0 B.1-2x+1=0C.1+2x-2=0 D.1-2x+2=02.当x=___时,代数式3(2-x)和2(3+x)的值相等.
(1) 11x+1 = 5(2x+1) ; (2)2-(1-x) = -2;
解: 去括号,得 11x+1 = 10x+5.移项,得 11x-10x = 5-1.
合并同类项,得 x= 4.
解: 去括号,得 2-1+x = -2.
移项,得 x=-2-2+1.
即
(3) 5(x+8) -5=0; (4) .
解: 两边同时除以5,得
移项,得
解: 去括号,得
两边同时除以16 ,得
2(4y + 3)=8( 1-y)
8y + 6=8-8y.
8y + 8y=8-6.
4.一个两位数,十位上的数字是个位上数字的2倍,将两个数字对调位置后得到的两位数比原来的数小36,原两位数是多少?
解:设这个两位数个位上的数字为x,则十位上的数字为2x.根据题意,得 (20x +x)-(10x+2x)=36.
所以这个两位数为20×4+4=84.
括号前面是负号,去括号时别忘记变号;括号前面有系数,去括号时别漏乘系数.
①去括号;②移项;③合并同类项;④系数化为1.
教科书 第138页习题5.4 第1、2题
2 求解一元一次方程第3课时
求解一元一次方程|去分母
1.掌握去分母的方法,完善解一元一次方程的一般步骤.2.会利用等式的基本性质2正确去分母解一元一次方程.3.通过总结概括一元一次方程的解法,进一步体会解方程过程中化归思想.4.通过对实际问题的探究,激发学生的学习兴趣和探究欲望,增强用数学的兴趣.
希腊数学家丢番图的墓碑上记载着: 他生命的六分之一是幸福的童年;再活了他生命的十二分之一,两鬓长起了细细的胡须;他结了婚,又度过了一生的七分之一;再过五年,他才有儿子,感到很幸福;可是儿子只活了他父亲全部年龄的一半;儿子死后,他在极度悲哀中度过了四年,也与世长辞了.
解:去分母,得 14x+7x+12x+420+42x+336=84x. 移项,得 14x+7x+12x+42x–84x=–336–420. 合并同类项,得 –9x= –756.方程两边同除以–9,得 x=84.
这两种解法有什么不同?
第一种解法用移项法求解;第二种解法先去分母,再用移项法求解.
第二种解法是如何去分母的呢?
利用等式的基本性质2,方程两边同乘分母的最小公倍数.
去括号,得 移项,得 合并同类项,得 方程两边同除以 (或同乘 ) ,得 x=–28.
在去括号解方程的方法基础上增加一步,先去分母,再解方程.
去分母,得 4( x+14)=7( x+20).去括号,得 4x+56=7x+140.移项,得 4x–7x=140–56.合并同类项,得 –3x= –84.方程两边同除以–3,得 x= –28.
4( x+14)=7( x+20). 4x+56=7x+140. 4x–7x=140–56. x = –28.
解一元一次方程有哪些步骤?
解一元一次方程,一般要通过去分母、去括号、移项、合并同类项、未知数的系数化为1等步骤,把一个一元一次方程“转化”成x=a的形式.
下列方程的解法对不对?如果不对,你能找出错在哪里吗? 解方程: 解:去分母,得 2(2x–1)–3(x + 2) = 1. 去括号,得 4x–1–3x+6=1. 移项,得 4x–3x=1+1–6. 合并同类项,得 x=4.
方程右边的“1”去分母时漏乘最小公倍数6.
去括号时,–3×2忘记变号
利用解一元一次方程的基本步骤求解,先去分母,去括号,再移项合并同类项,系数化为1.
去分母,得 6( x+15)=15–10( x–7).去括号,得 6x+90=15–10x+70.移项,得 6x+10x=15+70–90.合并同类项,得 16x= –5.方程两边同除以16,得
1. 方程 去分母正确的是 ( ) A. 3–2(5x+7) = –(x+17) B. 12–2(5x+7) = –x+17 C. 12–2(5x+7) = –(x+17) D. 12–10x+14 = –(x+17)
解: 去分母,得 3(3–x) = 2(x+4).去括号,得 9–3x = 2x+8.
移项,合并同类项,得 5x= 1.方程两边同时除以5,得
解: 去分母,得 7(x+1) = 3(2x–3).去括号,得 7x+7 = 6x–9.
移项,合并同类项,得 x= –16.
解: 去分母,得 4(2x–1) = 3(x+2)–12.去括号,得 8x–4 = 3x+6–12.
移项,合并同类项,得 5x= –2. 方程两边同时除以5,得
解: 去分母,得 5(x–1) = 20–2(x+2).去括号,得 5x–5 = 20–2x–4.
移项,合并同类项,得 7x=21.方程两边同时除以7,得x=3.
4.小川今年6岁,他的祖父72岁,几年后小川的年龄是他祖父年龄的 ?
解:设x年后小川的年龄是他祖父年龄的 .根据题意,得
所以16年后小川的年龄是他祖父年龄的 .
(1)依据:等式性质2.(2)方程两边乘以各分母的最小公倍数时,注意: ①不漏乘不含分母的项;②注意给分子添括号、去括号.
①去分母;②去括号;②移项;③合并同类项;④系数化为1.
教科书 第140页习题5.5 第1、3题
相关课件
这是一份初中数学北师大版七年级上册5.2 求解一元一次方程获奖教学ppt课件,共23页。PPT课件主要包含了得x=-28,解方程,这样做的依据是什么,例2对解方程,去分母,等式性质2,随堂练习,没有乘以10,-x+33x,去括号得等内容,欢迎下载使用。
这是一份北师大版七年级上册5.2 求解一元一次方程评优课教学ppt课件,共23页。PPT课件主要包含了学习新知,复习巩固,探究新知,x+2+x=17,x=3,去括号,合并同类项,x+x=17-2,系数化为1,x=15等内容,欢迎下载使用。
这是一份北师大版5.2 求解一元一次方程优秀教学ppt课件,共20页。PPT课件主要包含了学习目标,复习巩固,探究新知,合并同类项,系数化为1,解移项得,合并同类项得,典型例题,22x+6=1,移项得等内容,欢迎下载使用。










