2023-2024学年江苏省南通市崇川区九年级（上）期中数学试卷（含解析）

这是一份2023-2024学年江苏省南通市崇川区九年级（上）期中数学试卷（含解析），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.抛物线y=(x−5)2+1的顶点坐标是
( )
A. (5,−1)B. (−5,1)C. (5,1)D. (−5,−1)
2.已知点P到圆心O的距离为5，若点P在圆内，则⊙O的半径可能为
( )
A. 3B. 4C. 5D. 6
3.反比例函数y=kx(k≠0)的图象经过点A(−2,3)，则此图象一定经过下列哪个点( )
A. (3,2)B. (−3,−2)C. (−3,2)D. (−2,−3)
4.二次函数y=ax2+bx+c的图像经过点−5,0，3,0，则关于x的方程ax2+bx+c=0的根是
( )
A. x1=0，x2=3B. x1=−5，x2=0
C. x1=5，x2=−3D. x1=−5，x2=3
5.如图，四边形ABCD是⊙O的内接四边形，若∠BOD=130°，则∠A的度数为( )
A. 50°B. 65°C. 115°D. 130°
6.已知反比例函数y=3x，当x>3时，y的取值范围是( )
A. y>−1B. y<1C. −17.如图，▵ABC是一张三角形纸片，⊙O是它的内切圆，点D、E是其中的两个切点，已知AD=6cm，小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形▵AMN，则剪下的▵AMN的周长是( )
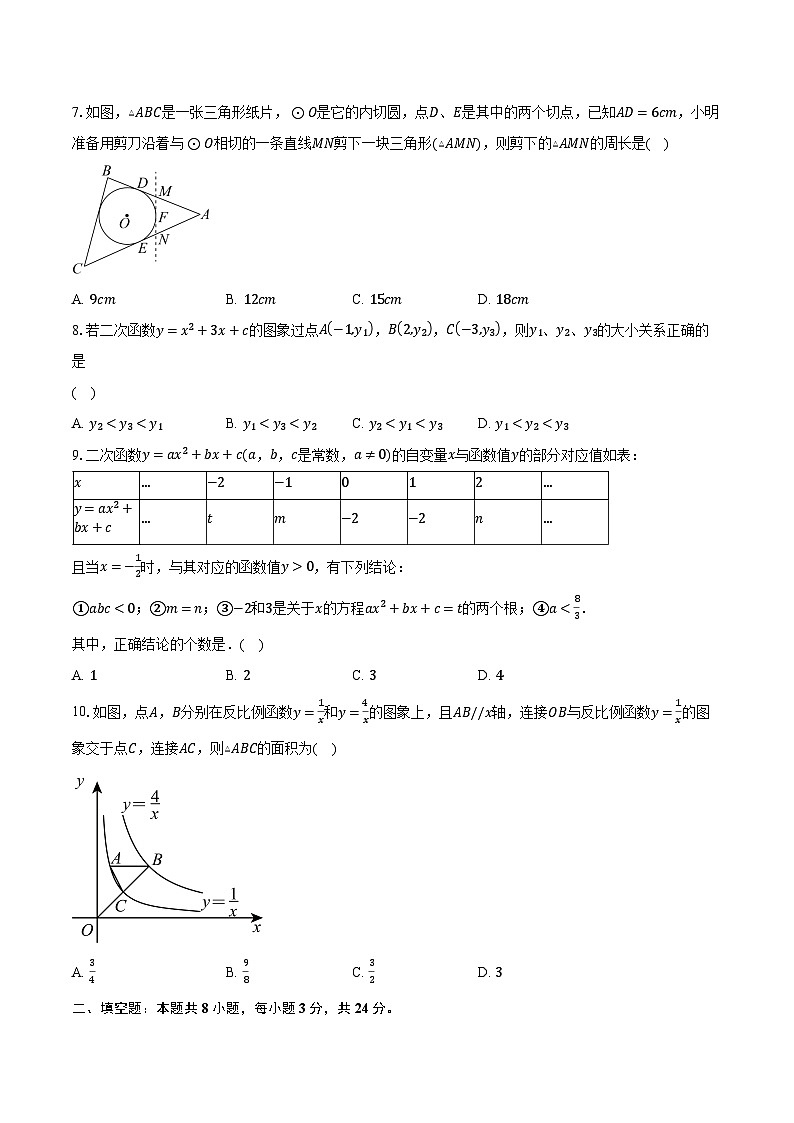
A. 9cmB. 12cmC. 15cmD. 18cm
8.若二次函数y=x2+3x+c的图象过点A−1,y1，B2,y2，C−3,y3，则y1、y2、y3的大小关系正确的是
( )
A. y29.二次函数y=ax2+bx+c(a，b，c是常数，a≠0)的自变量x与函数值y的部分对应值如表：
且当x=−12时，与其对应的函数值y>0，有下列结论：
①abc<0；②m=n；③−2和3是关于x的方程ax2+bx+c=t的两个根；④a<83．
其中，正确结论的个数是．( )
A. 1B. 2C. 3D. 4
10.如图，点A，B分别在反比例函数y=1x和y=4x的图象上，且AB/​/x轴，连接OB与反比例函数y=1x的图象交于点C，连接AC，则▵ABC的面积为( )
A. 34B. 98C. 32D. 3
二、填空题：本题共8小题，每小题3分，共24分。
11.若双曲线y=k−1x的图像经过第一、三象限，则k的取值范围是____．
12.一个正多边形的中心角是40∘，则这个正多边形的边数为________．
13.将抛物线y=x2向上平移3个单位，向左移动1个单位，所得抛物线的解析式是___________．
14.用一个圆心角为150°，半径为12的扇形作一个圆锥的侧面，则这个圆锥的底面半径为_____．
15.如图，A是反比例函数y=kx的图象上一点，AB⊥y轴于点B，若▵ABO的面积为2，则k的值为_____．
16.如图，物体从点A抛出，物体的高度y(单位：m)与飞行时间t(单位：s)近似满足函数关系式y=−15(t−3)2+5.在飞行过程中，若物体在某一个高度时总对应两个不同的时间，则t的取值范围是______．
17.如图，正方形ABCD的边长为6，以BC为直径的半圆O交对角线AC于点E，则阴影部分的面积是______．
18.已知实数m，n满足m2−am+1=0，n2−an+1=0，且m≠n，若a≥3，则代数式m−12+n−12的最小值是____．
三、解答题：本题共8小题，共64分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题8分)
如图所示的拱桥，用弧AB表示桥拱．

(1)若弧AB所在圆的圆心为O，EF是弦CD的垂直平分线，请你利用尺规作图，找出圆心O.(不写作法，但要保留作图痕迹)
(2)若拱桥的跨度(弦AB的长)为16m，拱高(弧AB的中点到弦AB的距离)为4m，求拱桥的半径R．
20.(本小题8分)
如图，已知二次函数y=x2+bx+c图象经过点A1,−2和B0,−5．

(1)求该二次函数的表达式及图象的顶点坐标；
(2)当−3≤x≤0时，求该二次函数的函数值y的取值范围．
21.(本小题8分)
如图，一次函数y=kx+b与反比例函数y=mx的图象交于点A(1,8)、B(n,−2)，与x轴交于点D，与y轴交于点C．
(1)求m、n的值；
(2)观察函数图象，直接写出不等式kx+b(3)连接AO，BO，求▵AOB的面积．
22.(本小题8分)
智能饮水机接通电源后开始自动加热，水温每分钟上升20，加热到100时，饮水机自动停止加热，水温开始下降．在水温开始下降的过程中，水温y 与通电时间min成反比例关系．当水温降至室温时，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20，接通电源后，水温y 与通电时间xmin之间的关系如图所示．

(1)求当4(2)加热一次，水温不低于40的时间有多长？
23.(本小题8分)
如图，C是⊙O被直径AB分成的半圆上一点，过点C的⊙O的切线交AB的延长线于点P，连接CA，CO，CB．
(1)求证：∠ACO=∠BCP；
(2)若∠ABC=2∠BCP，AB=4，求图中阴影部分的面积(结果保留π和根号)．
24.(本小题8分)
某商店销售某种商品的进价为每件20元，这种商品在近30天中的日销售价与日销量的相关信息如表：
设该商品的日销售利润为w元．
(1)求出w与x的函数关系式；
(2)该商品在第几天的日销售利润最大？最大日销售利润是多少？
25.(本小题8分)
【问题情境】
如图1，P是⊙O外一点，直线PO分别交⊙O于A，B两点，则PA的长是点P到⊙O上的点的最短距离．

【初步探究】
如图2，小明为了证明【问题情境】中的结论，给出如下思路：在⊙O上任取一点C(不与A，B两点重合)，连接PC，OC.请你根据小明的思路继续思考，完成PA
【直接运用】
如图3，在Rt▵ABC中，∠ACB=90∘，AC=BC=4，以BC为直径的半圆交AB于点D，P是CD⌢上的一个动点，连接AP，求出线段AP长度的最小值；

【构造运用】
如图4，在正方形ABCD中，AD=6，点E，F分别从D，C两点同时出发，以相同的速度在边DC，CB上移动，连接AE和DF交于点P，由于点E，F的移动，使得点P也随之运动，请求出线段CP长度的最小值．
26.(本小题8分)
已知抛物线W1：y=ax2−4ax−4(a为常数，且a≠0)有最低点．
(1)求二次函数y=ax2−4ax−4的最小值(用含a的式子表示)；
(2)将抛物线W1向右平移a个单位得到抛物线W2.经过探究发现，随着a的变化，抛物线W2顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；
(3)记(2)所求的函数图象为H，抛物线W1与H交于点P，设点P的纵坐标为n，结合图象，求n的取值范围．
答案和解析
1.【答案】C
【解析】【分析】直接根据二次函数的顶点式即可求解．
【详解】解：抛物线y=(x−5)2+1的顶点坐标是(5,1)．
故选：C．
本题考查了二次函数的性质，二次函数的顶点式为y=a(x−k)2+h，则抛物线的对称轴为直线x=k，顶点坐标为(k,h) .
2.【答案】D
【解析】【分析】由点与圆的位置关系可知，⊙O的半径r>5，进而可得出结果．
【详解】解：由点与圆的位置关系可知，⊙O的半径r>5
故选D．
本题考查了点与圆的位置关系．解题的关键在于对知识的熟练掌握．
3.【答案】C
【解析】【分析】根据反比例函数图象上点的坐标特征即可求解．
【详解】解：∵反比例函数y=kx(k≠0)的图象经过点A(−2,3)，
∴k=−2×3=−6，
A.−3×2=6≠−6，图象不经过点(3,2)；
B.−3×(−2)=6≠−6，图象不经过点(−3,−2)；
C.−3×2=−6，图象经过点(−3,2)；
D.−2×(−3)=6≠−6，图象不经过点(−2,−3)；
∴C选项符合题意，
故选：C．
本题考查了反比例函数图象上点的坐标特征，解题的关键是根据A点的坐标求出k值．
4.【答案】D
【解析】【分析】根据抛物线与x轴交点的横坐标是令y=ax2+bx+c=0的两个根，计算判断即可．
【详解】因为二次函数y=ax2+bx+c的图像经过点−5,0，3,0，
所以方程ax2+bx+c=0的根是x1=−5，x2=3，
故选D．
本题考查了抛物线与x轴的交点，熟练掌握抛物线与一元二次方程的关系是解题的关键．
5.【答案】C
【解析】【分析】先根据圆周角定理求出∠BCD的度数，再根据圆的内接四边形对角互补的性质求出结果．
【详解】解：∵∠BOD=130∘，
∴∠BCD=12∠BOD=65∘，
∵四边形ABCD是⊙O的内接四边形，
∴∠A+∠BCD=180∘，
∴∠A=115∘．
故选：C．
本题考查圆的内接四边形的性质，解题的关键是掌握圆的内接四边形对角互补的性质．
6.【答案】D
【解析】略
7.【答案】B
【解析】【分析】根据切线长定理，得到AE=AD=6cm，MD=MF，NE=NF，再利用三角形周长公式即可得到答案．
【详解】解：∵AD、AC、MN都是⊙O的切线，
∴AE=AD=6cm，MD=MF，NE=NF，
∴▵AMN的周长=AM+MF+NF+AN=AM+MD+AN+NE=AD+AE=6+6=12cm，
故选B．
本题考查了内切圆的性质，切线长定理，解题关键是熟练掌握切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分这两条切线的夹角．
8.【答案】B
【解析】【分析】根据二次函数的性质得到抛物线y=x2+3x+c的开口向上，对称轴为直线x=−1.5，然后根据三个点离对称轴的远近判断函数值的大小．
【详解】解：∵抛物线y=x2+3x+c=(x+1.5)2−1.52+c
∴抛物线开口向上，对称轴为直线x=−1.5，
∵B2,y2离直线x=−1.5的距离最远，A−1,y1点离直线x=−1.5最近，
∴y1故选B．
本题考查了二次函数图象与性质，熟练掌握二次函数的性质是解题的关键．
9.【答案】B
【解析】【分析】根据二次函数的性质逐一进行分析即可
【详解】解：①函数的对称轴为：x=12(0+1)=12，则ab<0，c=−2<0，故abc>0，故①错误，不符合题意；
②根据表格可得：x=−1和x=2关于函数对称轴对称，故m=n正确，符合题意；
③函数的对称轴为：x=12，根据表格可得：x=−2和x=3关于函数对称轴对称，此时的函数值为t，则−2和3是关于x的方程ax2+bx+c=t的两个根，故③正确，符合题意；
④函数的对称轴为：x=12，则b=−a，当x=−12时，y=14a−12b−2>0，所以3a−8>0，故④错误，不符合题意；
故选：B．
本题考查的是二次函数图象与系数的关系，熟悉函数的基本性质，能熟练求解函数与坐标轴的交点及顶点的坐标等．
10.【答案】A
【解析】【分析】设A(a,1a)，则B(4a,1a)，再利用待定系数法求得直线OB的解析式，与函数y=1x联立成方程组，解方程组即可求得C的坐标，然后代入三角形面积公式求解即可．表示出A、B、C的坐标是解题的关键
【详解】解：设A(a,1a)，则B(4a,1a)，
∴直线OB为y=14a2x，
由y=14a2xy=1x，解得x=2ay=12a,
∴C(2a,12a)，
∴S▵ABC=124a−a⋅1a−12a=34
故选：A．

11.【答案】k>1##1【解析】【分析】本题主要考查了反比例函数的图像与性质、解一元一次不等式．根据该双曲线的图像经过第一、三象限，可得k−1>0，解不等式，即可获得答案．
【详解】解：∵双曲线y=k−1x的图像经过第一、三象限，
∴k−1>0，
解得k>1．
故答案为：k>1．
12.【答案】九##9
【解析】【分析】根据正多边形的每个中心角相等，且所有中心角的度数和为360°进行求解即可．
【详解】解：设这个正多边形的边数为n，
∵这个正多边形的中心角是40°，
∴40∘⋅n=360∘，
∴n=9，
∴这个正多边形是九边形，
故答案为：九．
本题主要考查了正多边形的性质，熟知正多边形中心角的度数和为360度是解题的关键．
13.【答案】y=x+12+3
【解析】【分析】根据题意可得将抛物线y=x2向上平移3个单位，再向左平移1个单位，所得抛物线的顶点坐标为−1,3，即可求解．
【详解】解：∵抛物线y=x2的顶点坐标为0,0，
∴将抛物线y=x2向上平移3个单位，再向左平移1个单位，所得抛物线的顶点坐标为−1,3，
∴所得抛物线的解析式是y=x+12+3．
故答案为：y=x+12+3．
本题主要考查了二次函数图象的平移，熟练掌握二次函数图象的平移的规律是解题的关键．
14.【答案】5
【解析】【分析】先计算出扇形的弧长，再利用圆的周长和圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长求解即可．
【详解】扇形的弧长=150π×12180=10π，
设圆锥的底面半径为R，则2πR=10π，解得R=5．
故答案为：5．
本题考查了圆锥的计算，理解圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长求解、扇形的半径和圆锥母线等长．
15.【答案】4
【解析】【分析】本题考查反比例函数的图象与性质，反比例函数图象上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积是12k.根据反比例函数比例系数的几何意义，即可得到S▵AOB=12k=2，计算出来即可．
【详解】根据题意可知：S▵AOB=12k=2，
∵反比例函数的图象位于第一、三象限，k>0，
∴k=4．
故答案为：4．
16.【答案】0≤t≤6且t≠3
【解析】【分析】本题考查了二次函数的图象及性质，当t=0时，得OA=165m，再当y=165时，解得t=0或t=6，进而可求解，熟练掌握二次函数的图象及性质是解题的关键．
【详解】解：由图得：
当t=0时，y=−15(t−3)2+5=−15(0−3)2+5=−95+5=165，
即OA=165m．
当y=165时，−15(t−3)2+5=165，
解得：t=0或t=6，
∴当0≤t≤6且t≠3时，物体在某一个高度时总对应两个不同的时间，
故答案为：0≤t≤6且t≠3．
17.【答案】18−94π
【解析】【分析】本题考查扇形的面积的计算、正方形的性质，解题的关键是根据题意和图形可知阴影部分的面积是▵ABC的面积减去弓形BE的面积，再减去▵OEC的面积，从而可以解答本题．
【详解】解：∵正方形ABCD边长为6，
∴AB=BC=CD=DA=6，
∵弓形BE和弓形CE的面积相等，
∴阴影部分的面积是：
12S△ABC−S弓形BE−S△OCE
=12S△ABC−S弓形CE+S△OCE
=12S△ABC−S扇形OEC
=12×6×6−14×32π
=18−94π，
故答案为：18−94π．
18.【答案】3
【解析】【分析】本题考查了一元二次方程根与系数的关系，二次函数的增减性，解题的关键是掌握一元二次方程ax2+bx+c=0a≠0根与系数关系：x1+x2=−ba,x1⋅x2=ca.根据m2−am+1=0，n2−an+1=0，得出m2+1=am,n2+1=an，以及实数m，n满足m2−am+1=0，n2−an+1=0，即可将m−12+n−12整理为a−2m+n，再根据一元二次方程根与系数的关系得出m+n=a，进而得出m−12+n−12=a−12−1，最后根据二次函数的增减性，即可解答．
【详解】解：∵m2−am+1=0，n2−an+1=0，
∴m2+1=am,n2+1=an，
∴m−12+n−12
=m2−2m+1+n2−2n+1
=am+an−2m−2n
=am+n−2m+n
=a−2m+n，
∵实数m，n满足m2−am+1=0，n2−an+1=0，且m≠n，
∴m、n可看作关于x的一元二次方程x2−ax+1=0的两根，
∴m+n=a，
∴m−12+n−12=aa−2=a2−2a=a−12−1，
∵1>0，
∴当a>1时，m−12+n−12的值随x的增大而增大，
∵a≥3，
∴当a=3时，m−12+n−12有最小值，最小值为3−12−1=3．
故答案为：3．
19.【答案】【小问1详解】
解：如图所示，作AB的垂直平分线GH，交EF于点O，
【小问2详解】
解：如图，

设M为AB⌢的中点，OM交AB于点N，
∵OM⊥AB，
∴AN=NB=8，MN=4，
设拱桥的半径为r，在Rt▵AON中，AO=r，ON=r−4，
∵AO2=AN2+ON2，
∴r2=82+r−42
解得：r=10
∴拱桥的半径为10米．

【解析】【分析】(1)作AB的垂直平分线GH，交EF于点，即可求解；
(2)根据垂径定理得出AN=NB=8，MN=4，设拱桥的半径为r，在Rt▵AON中，勾股定理即可求解．
本题考查了确定圆心的位置，垂径定理的应用，掌握以上知识是解题的关键．
20.【答案】【小问1详解】
解：把A1,−2和B0,−5代入y=x2+bx+c，得：
1+b+c=−2c=−5，解得：b=2c=−5,
∴y=x2+2x−5，
∴y=x2+2x−5=x+12−6，
∴顶点坐标为−1,−6；
【小问2详解】
∵y=x2+2x−5=x+12−6，
∴抛物线的开口向上，对称轴为直线x=−1，
∴抛物线上的点离对称轴越远，函数值越大，
∵−3≤x≤0，
∴当x=−3时，y有最大值为：−3+12−6=−2，当x=−1时，y有最小值为：−6，
∴−6≤y≤−2．

【解析】【分析】本题考查二次函数的图象和性质．
(1)待定系数法求出函数解析式，转化为顶点式，求出顶点坐标；
(2)根据二次函数的性质，进行求解即可．
熟练掌握二次函数的 图象和性质，是解题的关键．
21.【答案】【小问1详解】
解：将A(1,8)代入y=mx中，得：8=m1
解得：m=8
∴ y=8x
将B(n,−2)代入y=8x，得：−2=8n
解得：n=−4．
【小问2详解】
解：根据图象可得，kx+b【小问3详解】
解：设直线AB的解析式为y=kx+b，将A(1,8)、B(−4,−2)代入y=kx+b得：k+b=8−4k+b=−2
解得：k=2b=6
∴直线AB的解析式为：y=2x+6
将x=0代入y=2x+6得y=6
∴C(0,6)，即OC=6，
连接OA,OB，
∴S▵AOB=S▵AOC+S▵BOC=12×6×1+12×6×4=15．

【解析】【分析】(1)将A(1,8)代入y=mx中，即可求出m的值，再代入B(n,−2)即可求得n的值；
(2)观察函数图象，即可得出kx+b(3)代入A点和B点坐标到y=kx+b即可求得直线AB的解析式，再令x=0，即可求出C(0,6)，根据S△AOB=S△AOC+S△BOC即可求出ΔAOB的面积．
本题主要考查一次函数与反比例函数的综合题型，懂得求反比例函数和一次函数的解析式，根据解析式求点坐标是解题的关键．
22.【答案】【小问1详解】
设反比例函数的表达式为：y=kx，
将点(4,100)代入反比例函数表达式得：k=4×100=400，
故函数的表达式为：y=400x，
当y=20时，y=400x=20，
则x=20=a，
即函数的表达式为：y=400x4≤x≤20；
【小问2详解】
设0≤x≤4时，函数的表达式为：y=mx+20，
将点(4,100)代入上式得：100=4m+20，
解得：m=20，
即一次函数的表达式为：y=20x+20，
令y=40，将其代入y=20x+20中，
解得：x=1，
在降温过程中，水温为40时，40=400x，
解得：x=10，
∵10−1=9，
∴一个加热周期内水温不低于40的时间为9min．

【解析】【分析】本题主要考查了反比例函数和一次函数的应用，解题的关键是看懂图像，灵活运用所学知识解决问题．
(1)当4(2)先求0≤x≤4时的函数解析式，再令y=40代入解析式中，解得x=1；在降温过程中，水温为40时，x=10，最后把两个时间值相减即可．
23.【答案】【小问1详解】
证明：∵AB是半圆O的直径，
∴∠ACB=90∘，
∵CP是半圆O的切线，
∴∠OCP=90∘，
∴∠ACB=∠OCP，
∴∠ACO=∠BCP；
【小问2详解】
解：由(1)知∠ACO=∠BCP，
∵∠ABC=2∠BCP，
∴∠ABC=2∠ACO，
∵OA=OC，
∴∠ACO=∠A，
∴∠ABC=2∠A，
∵∠ABC+∠A=90∘，
∴∠A=30∘，
∵∠ACB=90∘，
∴BC=12AB=2，AC= 3BC=2 3，
∴S▵ABC=12BC⋅AC=12×2×2 3=2 3，
∴阴影部分的面积是12π×AB22−2 3=2π−2 3，
答：阴影部分的 面积是2π−2 3．

【解析】【分析】(1)由AB是半圆O的直径，CP是半圆O的切线，可得∠ACB=∠OCP，即得∠ACO=∠BCP；
(2)由∠ABC=2∠BCP得∠A=30∘，可得BC=12AB=2，AC= 3BC，即得S▵ABC，再利用阴影部分的面积等于半圆减去S▵ABC即可解题．
此题考查了圆的切线性质，含30∘角的直角三角形的性质，圆周角定理，求扇形面积，综合运用以上知识是解题的关键．
24.【答案】【小问1详解】
当1≤x≤22时，
w=0.5x+25−20120−2x=−x2+50x+600，
当23≤x≤30时，
w=36−20120−2x=−32x+1920，
∴w与x的函数关系式w=−x2+50x+6001≤x≤22−32x+192023≤x≤30,
故答案为：w=−x2+50x+6001≤x≤22−32x+192023≤x≤30；
【小问2详解】
当1≤x≤22时，
w=−x2+50x+600=−x−252+1225，
∵−1<0，
∴当x=22时，w有最大值，最大值为 1216；
当23≤x≤30时，w=−32x+1920，
∵−32<0，
∴当x=23时，w有最大值，最大值为−32×23+1920=1184，
∵1216>1184，
∴该商品在第22天的日销售利润最大，最大日销售利润是1216元．

【解析】【分析】本题考查二次函数的应用、一次函数的应用，列出函数表达式是解题的关键．
(1)分1≤x≤22和23≤x≤30两种情况利用“利润=每件的利润×销售量”列出函数关系式；
(2)根据(1)解析式，由函数的性质分别求出1≤x≤22的函数最大值和23≤x≤30的函数最大值，比较得出结果．
25.【答案】【详解】初步探究：
证明：∵PO=PA+OA，PO∴PA直接运用：
解：取BC 的 中点E，连接AE，交半圆于P2，在半圆上任取P1，连接AP1，EP1，可见，AP1+EP1>AE，即AP2是AP的最小值．

在Rt▵ABC中，∠ACB=90∘，AC=BC=4，CE=12BC=2，
∴AE= AC2+CE2=2 5，
∵P2E=2，
∴AP2=2 5−2；
即AP长度的最小值为2 5−2．
构造运用：
解：如图，

∵四边形ABCD是正方形，
∴AD=DC=6，∠ADC=∠C=90∘，
在▵ADE和▵DCF中，
AD=DC∠ADC=∠CDE=CF,
∴△ADE≌△DCF(SAS)，
∴AE=DF，∠DAE=∠CDF，
∵∠CDF+∠ADF=90∘，
∴∠DAE+∠ADF=90∘．
∴AE⊥DF；
由于点P在运动中保持∠APD=90∘，
∴点P的路径是一段以AD为直径的弧，
设AD的中点为Q，连接QC交弧于点P，此时CP的长度最小，
在Rt▵QDC中，QC= 62+32=3 5，
∴CP=QC−QP=3 5−3．
答：线段CP的最小值为3 5−3．

【解析】【分析】初步探究：本题考查连点间线短距离最短，根据两点间线短距离最短结合半径相等即可得到答案；
直接运用：本题考查圆外一点与圆上点最小距离问题，连接圆心与圆外点交圆于一点即为最小距离点，结合勾股定理求解即可得到答案；
构造运用：先证明▵ADE≌▵DCF得到定角∠APD=90∘，即可得到点P的路径是一段以AD为直径的弧，结合最短距离问题及勾股定理即可得到答案；
本题主要考查圆外一点到圆上点最小距离问题，勾股定理，三角形全等的判定与性质，解题的关键是找到最小距离点及定直角得到动点在圆上．
26.【答案】【小问1详解】
解：∵y=ax2−4ax−4=ax−22−4a−4，抛物线有最低点，
∴抛物线开口向上，二次函数y=ax2−4ax−4的最小值为−4a−4；
【小问2详解】
解：∵抛物线W1：y=ax−22−4a−4，
∴平移后的抛物线W2：y=ax−2−a2−4a−4，
∴抛物线W2顶点坐标为a+2,−4a−4，
∴x=a+2,y=−4a−4，
∴4x+y=4a+8−4a−4=4，
即4x+y=4，变形得y=−4x+4，
∵a>0，x=a+2，
∴x>2，
∴y与x的函数关系式为y=−4x+4x>2；
【小问3详解】
解：如图，∵抛物线W1：y=ax2−4ax−4，
当x=2时，y=−4a−4，
当x=4时，y=4a−4a−4=−4，
∴抛物线W1恒过点4,−4，
∵H：y=−4x+4x>2图象为射线，
当x=2时，y=−8+4=−4，
当x=4时，y=−16+4=−12，
∴函数H的图象过点4,−12，
由图象可知，若抛物线与函数H的图象有交点P，则yB∴点P纵坐标的取值范围为−12

【解析】【分析】本题考查了求二次函数的最值，二次函数的平移规律“左加右减，上加下减”，以及二次函数和一次函数的交点问题．
(1)将W1的函数表达式化为顶点式，即可求解；
(2)根据二次函数的平移规律：左减右加，上加下减，得出W2：y=ax−2−a2−4a−4，则W2顶点坐标为a+2,−4a−4，即可得出4x+y=4，根据二次函数开口向上，得出a>0，即可得出x的取值范围；
(3)求出抛物线W1恒过点4,−4，函数H的图象过点4,−12，由图象可知，若抛物线与函数H的图象有交点P，则yBx
…
−2
−1
0
1
2
…
y=ax2+bx+c
…
t
m
−2
−2
n
…
时间：第x(天)(1≤x≤30，x为整数)
1≤x≤22
23≤x≤30
日销售价(元/件)
0.5x+25
36
日销售量(件)
120−2x