初中数学18.1.2 平行四边形的判定课文ppt课件

这是一份初中数学18.1.2 平行四边形的判定课文ppt课件，共28页。PPT课件主要包含了定义判定，书写格式为，命题证明等内容，欢迎下载使用。

1.理解并掌握用边、角、对角线来判定平行四边形的方法．（重点）2.会综合运用平行四边形的判定方法和性质来解决问题．（难点）
两组对边分别平行的四边形，叫做平行四边形.
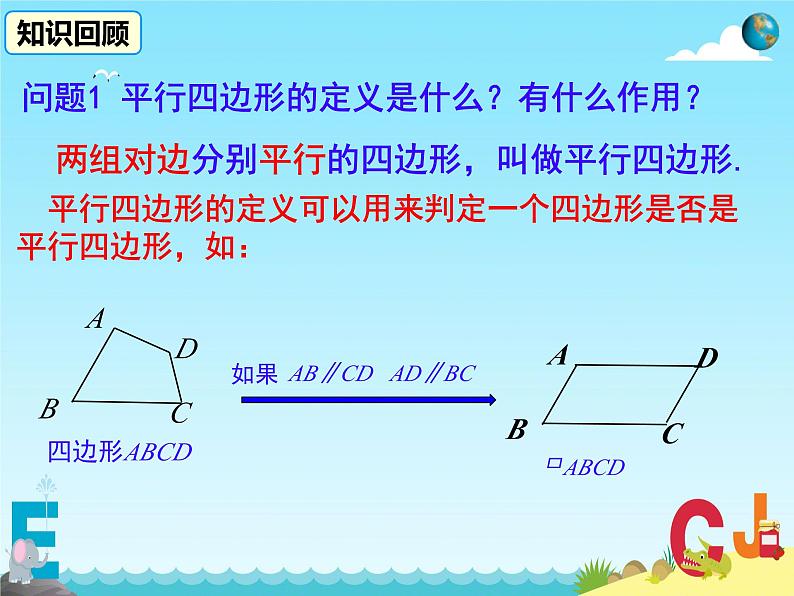
问题1 平行四边形的定义是什么？有什么作用？
平行四边形的定义可以用来判定一个四边形是否是平行四边形，如：
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
问题2 除了两组对边分别平行外，平行四边形还有哪些性质？
问题3 平行四边形上面的三条性质的逆命题各是什么？
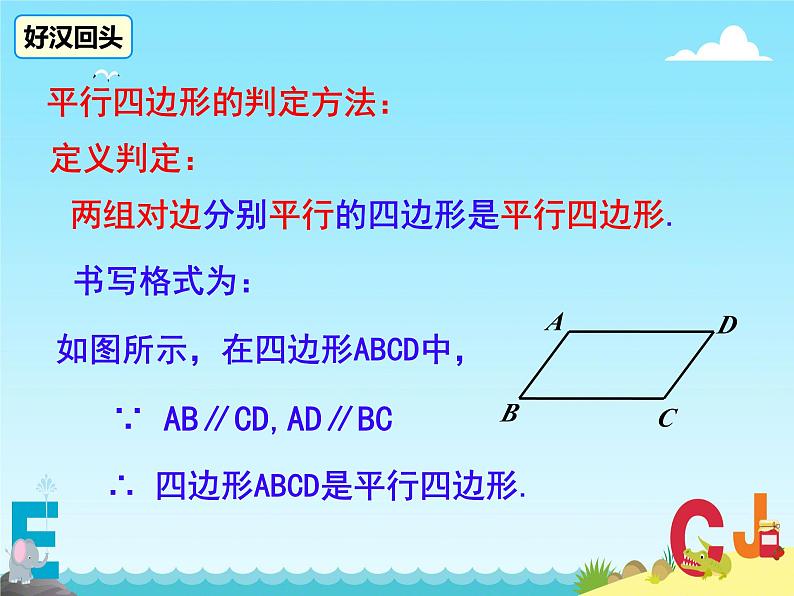
平行四边形的判定方法：
两组对边分别平行的四边形是平行四边形.
∴ 四边形ABCD是平行四边形.
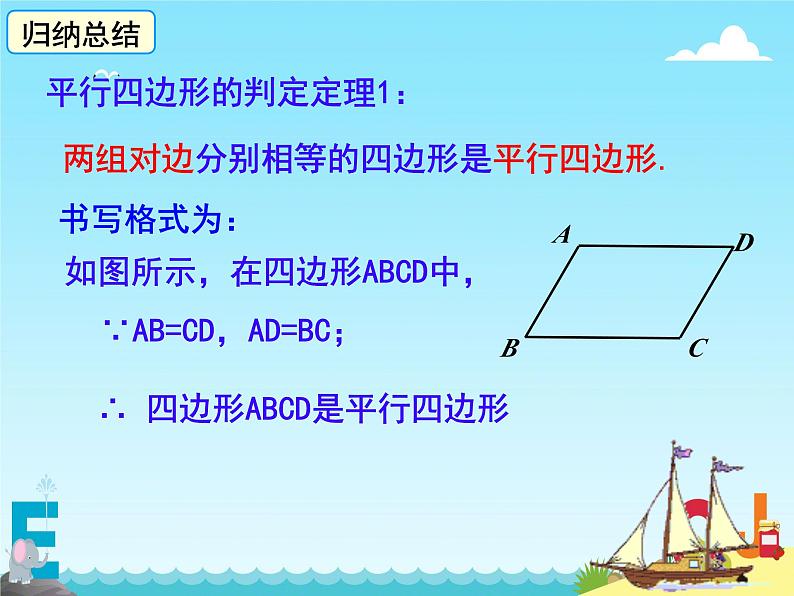
如图所示，在四边形ABCD中，
∵ AB∥CD,AD∥BC
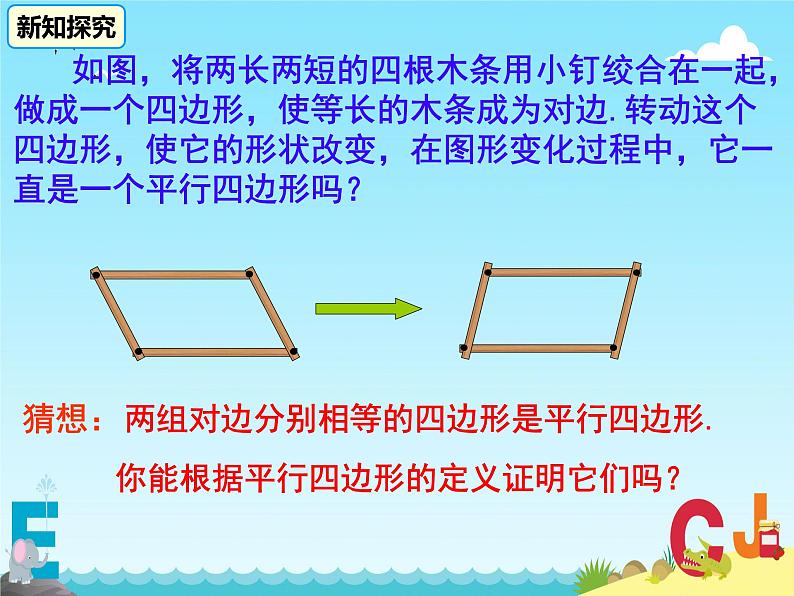
如图，将两长两短的四根木条用小钉绞合在一起，做成一个四边形，使等长的木条成为对边.转动这个四边形，使它的形状改变，在图形变化过程中，它一直是一个平行四边形吗？
两组对边分别相等的四边形是平行四边形.
你能根据平行四边形的定义证明它们吗？
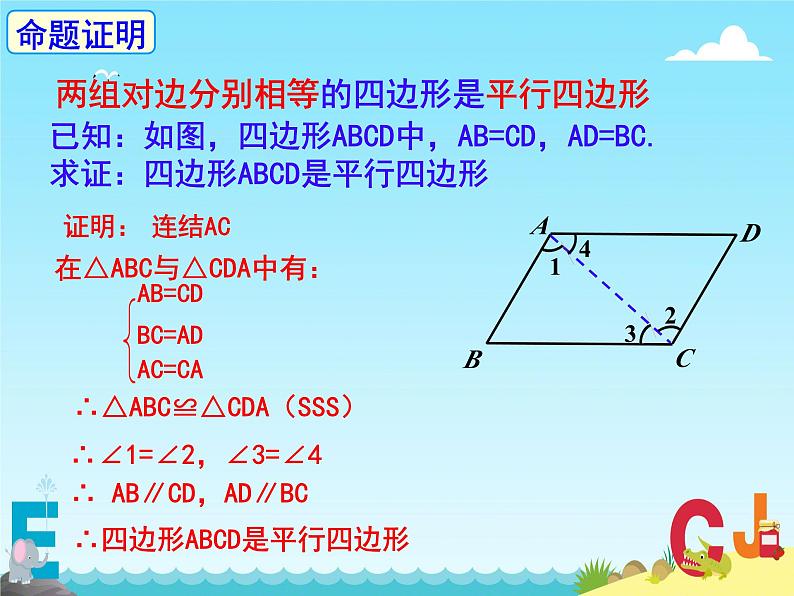
两组对边分别相等的四边形是平行四边形
已知：如图，四边形ABCD中，AB=CD，AD=BC.求证：四边形ABCD是平行四边形
在△ABC与△CDA中有：
∴△ABC≌△CDA（SSS）
∴∠1=∠2，∠3=∠4
∴ AB∥CD，AD∥BC
∴四边形ABCD是平行四边形
两组对边分别相等的四边形是平行四边形.
∴ 四边形ABCD是平行四边形
平行四边形的判定定理1：
∵AB=CD，AD=BC；
例1 如图所示，在四边形ABCD中，E，F分别是边AB，CD的中点，若△ADE≌△CBF，求证：四边形ABCD是平行四边形.
∵△ADE≌△CBF；
∴ AD=BC,DE=BF,AE=CF;
又∵E，F分别是边AB，CD的中点；
∴ 2AE=AB,2CF=CD;
∴ 四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形
如图，已知四边形ABCD中，∠A=∠C，∠B=∠D.试问：四边形ABCD是平行四边形吗？
用直尺量一量，并猜想你得到的结论.
如图，已知，在四边形ABCD中,∠A=∠C，∠B=∠D求证：四边形ABCD是平行四边形
∴四边形ABCD是平行四边形.
在四边形ABCD中，有：
∴ 2∠A+ 2∠B=360 °
∵∠A=∠C，∠B=∠D
即：∠A +∠B=180 °
∠A+∠B+∠C+∠D=360 °
平行四边形的判定定理2：
两组对角分别相等的四边形是平行四边形.
∴四边形ABCD是平行四边形．
例2 如图所示，在四边形ABCD中，∠B=∠D,∠1=∠2，求证：四边形ABCD是平行四边形.
∴△ABC≌△CDA（AAS）
∴∠BCA=∠DAC,
∴∠BCA+∠2=∠DAC+∠1,
即：∠BCD=∠DAB,
如图，将两根木条AC、BD的中点重叠，用小钉绞合在一起，用橡皮筋连接木条的顶点，做成一个平行边形ABCD，转动两根木条，四边形ABCD一直是一个平行四边形吗？
对角线互相平分的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
如图，已知在四边形ABCD中,对角线AC、BD交于点O，且OA=OC，OB=OD.求证：四边形ABCD是平行四边形.
在△AOD与△COB中有：
∴ △AOD≌△COB（SAS）
同理可证：AB∥CD
平行四边形的判定定理3：
∵OA=OC，OB=OD
∴ 四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形
∴ AO=CO，BO=DO;
∴AO-AE=CO-CF;
例3 已知：如图所示，▱ABCD的对角线AC 、BD 交于点O， E、F是AC上的两点，并且AE=CF. 求证：四边形BFDE是平行四边形
如图，将线段AB向右平移BC长度后得到线段DC，连接AD，BC，由此你能猜想四边形ABCD的形状吗？
四边形ABCD是平行四边形
猜想：一组对边平行且相等的四边形是平行四边形.
已知：如图，在四边形ABCD中，AB∥CD，AB=CD，求证：四边形ABCD是平行四边形.
∴△ABC≌△CDA．
(全等三角形的对应边相等)
平行四边形的判定定理4：
一组对边平行且相等的四边形是平行四边形.
特别强调：必须是同一组对边平行且相等.
例4 如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC． 求证：四边形BFCE是平行四边形．
∴四边形BFCE是平行四边形．
∴AB+BC=CD+BC，
在△ACE和△DBF中，有：
∴△ACE≌△DBF(SAS)，
∴∠ACE=∠DBF，
平行四边形的证明思路：
1.已知一组对边平行：
1）可以证明另一组对边也互相平行，利用定义判定证明.
2）可以证明平行的这一组对边相等，利用判定定理4证明.
2.已知一组对边相等：
1）可以证明另一组对边也相等，利用判定定理1证明.
2）可以证明相等的这一组对边平行，利用判定定理4证明.
3.已知一组对角相等：
4.已知一条对角线平分：
可以证明另一组对角也分别相等，利用判定定理2证明.
可以证明另一条对角线也平分，利用判定定理3证明.
1.如图，四边形ABCD的对角线交于点O，下列哪组条件不能判断四边形ABCD是平行四边形（　　） A．OA=OC，OB=OD B．AB=CD，AO=CO C．AB=CD，AD=BC D．∠BAD=∠BCD，AB∥CD
2.已知AD//BC ，要使这个四边形ABCD为平行四边形，需要增加条件_____ .
AD=BC或AB//CD
1.请你识别下列四边形哪些是平行四边形?为什么？
2.如图，▱ABCD中，E、F分别是边BC、DA上的点，且BE=DF. 求证：四边形AECF是平行四边形.
3.已知：如图，在四边形 ABCD中，对角线AC和BD相交于O，AO=OC，BA⊥AC，DC⊥AC.求证：四边形ABCD是平行四边形.
4．已知：如图，▱ABCD中，点E、F分别在CD、AB上，DF∥BE，EF交BD于点O． 求证：EO=OF．