



所属成套资源:-2023-2024学年七年级数学下册同步课件(北师大版)
初中数学北师大版七年级下册1 用表格表示的变量间关系教学ppt课件
展开这是一份初中数学北师大版七年级下册1 用表格表示的变量间关系教学ppt课件,共24页。PPT课件主要包含了学习目标,导入新课,新知探究,典例精析,当堂练习,不断加快,课堂小结等内容,欢迎下载使用。
1.了解常量与变量的含义,能分清实例中的常量与变量;了解自变量与因变量的意义;(重点)2.能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,尝试对变化趋势进行初步的预测.(难点)
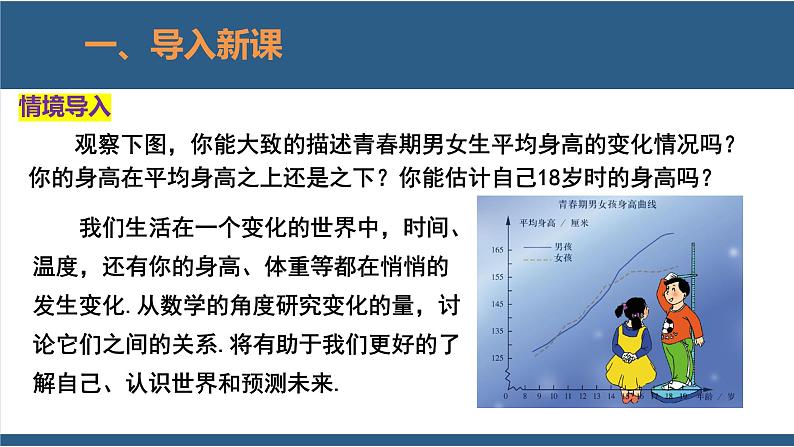
观察下图,你能大致的描述青春期男女生平均身高的变化情况吗?你的身高在平均身高之上还是之下?你能估计自己18岁时的身高吗?
我们生活在一个变化的世界中,时间、温度,还有你的身高、体重等都在悄悄的发生变化.从数学的角度研究变化的量,讨论它们之间的关系.将有助于我们更好的了解自己、认识世界和预测未来.
你还能从生活中举出一些发生变化的例子吗?
在本章,你还要学习到很多有用或有意思的变化,如骆驼体温的变化、潮汐的变化、记忆遗忘的规律、人口变化的规律等.
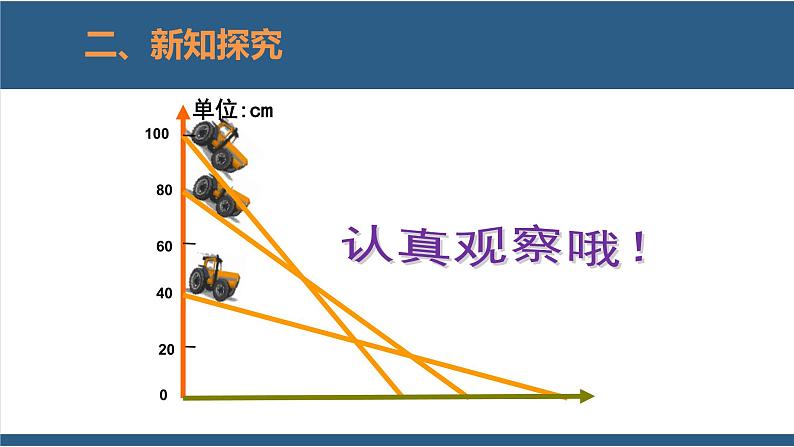
王波学习小组做了一个实验:小车下滑的时间.
这个小组利用同一块木板,测量小车从不同的高度下滑的时间,然后将得到的数据填入下表:
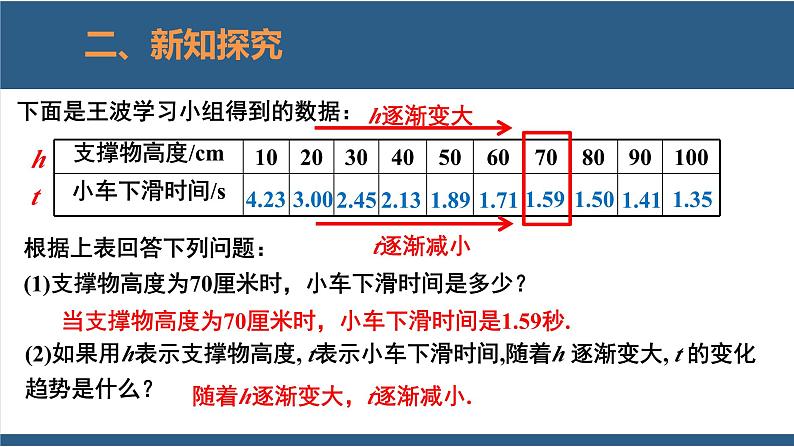
下面是王波学习小组得到的数据:
当支撑物高度为70厘米时,小车下滑时间是1.59秒.
(2)如果用h表示支撑物高度, t表示小车下滑时间,随着h 逐渐变大, t 的变化趋势是什么?
随着h逐渐变大,t逐渐减小.
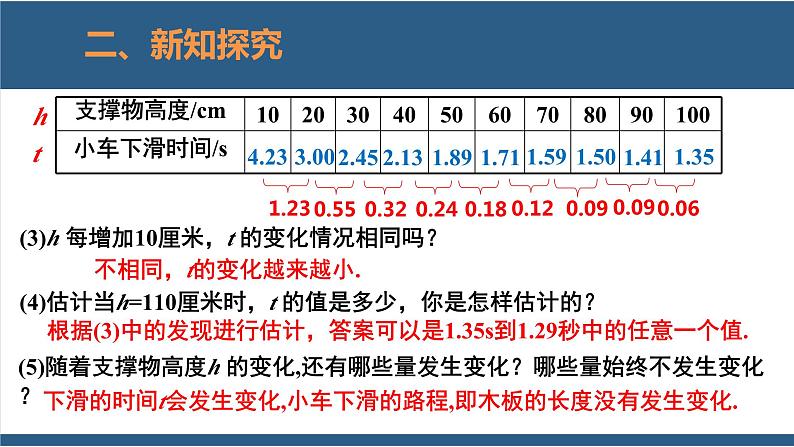
(3)h 每增加10厘米,t 的变化情况相同吗?
(4)估计当h=110厘米时,t 的值是多少,你是怎样估计的?
不相同,t的变化越来越小.
(5)随着支撑物高度h 的变化,还有哪些量发生变化?哪些量始终不发生变化?
根据(3)中的发现进行估计,答案可以是1.35s到1.29秒中的任意一个值.
下滑的时间t会发生变化,小车下滑的路程,即木板的长度没有发生变化.
在“小车下滑的时间”中,支撑物的高度h 和小车下滑的时间t 都在变化,它们都是变量.其中小车下滑的时间t 随支撑物的高度h 的变化而变化.支撑物的高度h 是自变量,小车下滑的时间t 是因变量. 在这一变化过程中,小车下滑的距离(木板的长度)一直没有变化.像这种在变化过程中数值始终不变的量叫作常量.
1.汽车以m千米/时的速度匀速从甲地驶向乙地,若甲、乙两地相距s千米,当汽车行驶了x小时后,距离乙地还有y千米,在这个问题中,常量是 ,变量是 ,其中自变量是 ,因变量是 .
注意:(1)自变量是在一定范围内主动变化的量.
(2)因变量是随自变量变化而变化的量.
随着x的增加,y也增加.
我国人口总数y随时间x的变化而变化,时间x是自变量,人口y是因变量.
探究二:用表格表示变量之间的关系
(3)从1949年起,时间每向后推移10年,我国人口是怎样变化的?
我国人口是逐渐增加的.从1949年起,时间每向后推10年,我国人口增加1.5亿左右.但最后10年的增加量大约只有0.76亿.
(4)你能根据此表格预测2019年时我国人口将会是多少?
注意:(1)借助表格,我们可以表示因变量随自变量的变化而变化的情况.(2)表格还能帮助我们对变化趋势进行初步的预测.
把自变量的一系列值和因变量的对应值列成一个表格来表示变量之间的关系,像这种表示变量之间关系的方法叫做表格法.
用表格表示变量间的关系
(1)上述的哪些量在发生变化?自变量和因变量各是什么?
年龄和体重在发生变化,自变量是年龄、因变量是体重.
例1:婴儿6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别约是1周岁时的2倍、3倍.
(2)某婴儿出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:
(3)根据表中的数据,说一说儿童从出生到10周岁之间体重是怎样随着年龄的增长而变化的.
从出生到10周岁,随年龄增长,儿童的体重在增加.
根据规律,高度每升高1千米,温度降低6℃,所以距离地面6千米时的温度是-10-6=-16(℃).
随着h的升高,t在降低.
1.假设汽车匀速行驶在高速公路上,那么在下列各量中,常量是( )A.行驶速度B.行驶时间C.行驶路程D.汽车油箱中的剩余油量
2.你坐在旋转的摩天轮上,那么你离开地面的高度随着时间的变化而变化.在这一问题中,因变量是( )A.摩天轮B.离开地面的高度C.时间D.自己
3.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(千瓦时)时,收取的电费为y(元).在这个问题中,下列说法正确的是( )A.x是自变量,0.6元/千瓦时是因变量 B.y是自变量,x是因变量C.0.6元/千瓦时是自变量,y是因变量 D.x是自变量,y是因变量
(2)当第10分钟提出新概念时,学生的接受能力为 .
解:(1)表中反映的是学生对新概念的接受能力与老师提出新概念所在的时间之间的关系.老师提出新概念所在的时间是自变量,学生对新概念的接受能力是因变量.
(3)根据表中的数据,你认为老师在第几分钟提出新概念,学生的接受能力最强?
(3)老师在第13分钟提出新概念,学生的接受能力最强.
(4)根据表中的数据,老师在哪段时间内提出新概念,学生的接受能力在逐渐增强?在哪段时间内提出新概念,学生的接受能力在逐渐减弱?
(4)老师在第0分钟到第13分钟内提出新概念,学生的接受能力在逐渐增强;在第13分钟到第26分钟内提出新概念,学生的接受能力在逐渐减弱.
相关课件
这是一份七年级下册1 用表格表示的变量间关系课文内容ppt课件,共27页。PPT课件主要包含了学习目标,情境导入,探究新知,变量与函数,单位cm,支撑物高度厘米,小车下滑时间秒,59秒,归纳总结,生活实例等内容,欢迎下载使用。
这是一份初中北师大版1 用表格表示的变量间关系备课课件ppt,共28页。PPT课件主要包含了59秒等内容,欢迎下载使用。
这是一份初中数学北师大版七年级下册第三章 变量之间的关系1 用表格表示的变量间关系图文ppt课件,共28页。PPT课件主要包含了变成了,探究篇,认知篇,知识巩固篇,生活链接接篇等内容,欢迎下载使用。













